协方差矩阵和相关系数矩阵是统计学中常用的概念,在多变量统计分析中起着至关重要的作用。
在进行多变量统计分析时,我们通常会涉及多个变量之间的关系和相互作用。协方差矩阵和相关系数矩阵就是用来描述这些变量之间的关系。
首先,我们来介绍协方差矩阵。协方差矩阵是一个对称矩阵,由变量间的协方差组成。协方差是度量两个随机变量间线性关系强度的指标,它描述了两个变量对于彼此的变化是如何同步的,也可以理解为两个变量之间的相关性。
协方差的计算公式为:
Cov(X,Y) = E[(X - μX)(Y - μY)]
其中,X和Y是两个变量,μX和μY分别是X和Y的均值,E[ ]表示期望。
如果两个变量X和Y的协方差为正值,则说明它们是正相关的,这意味着当X的值增加时,Y的值也会增加。相反,如果协方差为负值,则说明它们是负相关的,当X的值增加时,Y的值会减小。如果协方差接近于0,则说明它们之间没有线性关系。
协方差矩阵可以看作是一个方阵,它的对角线上的元素是每个变量的方差,而非对角线上的元素是对应变量之间的协方差。
下面我们来介绍相关系数矩阵。相关系数矩阵是协方差矩阵的归一化形式,用来度量变量之间线性关系的强度。
相关系数的计算公式为:
ρ(X,Y) = Cov(X,Y) / (σX * σY)
其中,ρ(X,Y)表示变量X和变量Y的相关系数,Cov(X,Y)是它们的协方差,σX和σY分别是变量X和变量Y的标准差。
相关系数的取值范围是-1到1之间,如果相关系数为1,则说明两个变量具有完全正相关关系;如果相关系数为-1,则说明两个变量具有完全负相关关系;如果相关系数接近于0,则说明它们之间没有线性关系。
相关系数矩阵也是一个对称矩阵,它的对角线上的元素是每个变量与自身的相关系数,而非对角线上的元素是对应变量之间的相关系数。
协方差矩阵和相关系数矩阵之间有一个重要的关系,就是相关系数矩阵是通过将协方差矩阵的每个元素除以对应的标准差得到的。
假设协方差矩阵为C,标准差向量为σ,那么相关系数矩阵可以表示为:
P = C / (σ * σ')
其中,P表示相关系数矩阵,'表示转置操作。
这种转换可以将协方差矩阵的值归一化到-1到1之间,更方便地判断变量之间的相关性。
协方差矩阵和相关系数矩阵在许多领域都有广泛应用。例如,在金融领域中,可以使用这些矩阵来评估相关证券之间的风险和相关性,以便进行资产组合的优化。在医学研究中,可以使用这些矩阵来检测不同因素之间的相关性和相互作用。在工程领域中,可以使用这些矩阵来评估不同变量之间的关联并进行系统优化。
总之,协方差矩阵和相关系数矩阵是用来描述多变量之间关系的重要工具。
-
协方差矩阵
+关注
关注
0文章
5浏览量
6039 -
元素
+关注
关注
0文章
47浏览量
8429 -
金融
+关注
关注
3文章
426浏览量
15912
发布评论请先 登录
相关推荐
Matlab协方差矩阵的计算原理
Matlab协方差矩阵的计算原理
基于协方差矩阵的CFA插值盲检测方法
基于协方差矩阵特征分解的多通道SAR-GMTI方法及性能分析
基于杂波协方差矩阵特征向量分析STAP降维方法
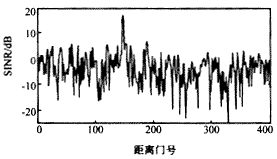
基于稀疏干扰协方差矩阵重构的稳健自适应波束形成算法(CAPON谱改正)
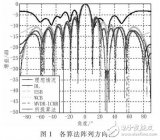
协方差矩阵是什么_协方差矩阵计算公式_如何计算协方差矩阵

什么是互相关函数?什么是相关系数?

基于协方差矩变异系数的能量泄露评估模型





 协方差矩阵和相关系数矩阵的转化
协方差矩阵和相关系数矩阵的转化










评论