哈夫曼编码是一种基于频率的变长编码方式,常用于数据压缩和信息传输领域。它是由美国数学家大卫·哈夫曼在1952年发明的,被广泛应用于无损压缩领域。
哈夫曼编码算法的基本思想是根据字符出现的频率构建一棵二叉树,将出现频率高的字符用较短的编码表示,而出现频率低的字符则用较长的编码表示。通过这种方式,可以实现对数据进行高效的编码和解码。
下面我们将详细介绍哈夫曼编码的算法过程。
- 统计字符频率
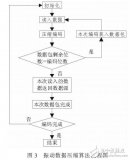
在进行哈夫曼编码前,首先需要统计字符出现的频率。这可以通过遍历待编码文本,计算每个字符的出现次数来实现。 - 构建哈夫曼树
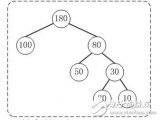
根据字符的频率,我们可以构建一棵哈夫曼树,其中每个叶子节点代表一个字符,节点的权重为字符的频率。构建哈夫曼树的过程可以采用贪心算法,即每次选择权重最小的两个节点合并,直到所有节点都合并为一棵树。 - 为每个字符分配编码
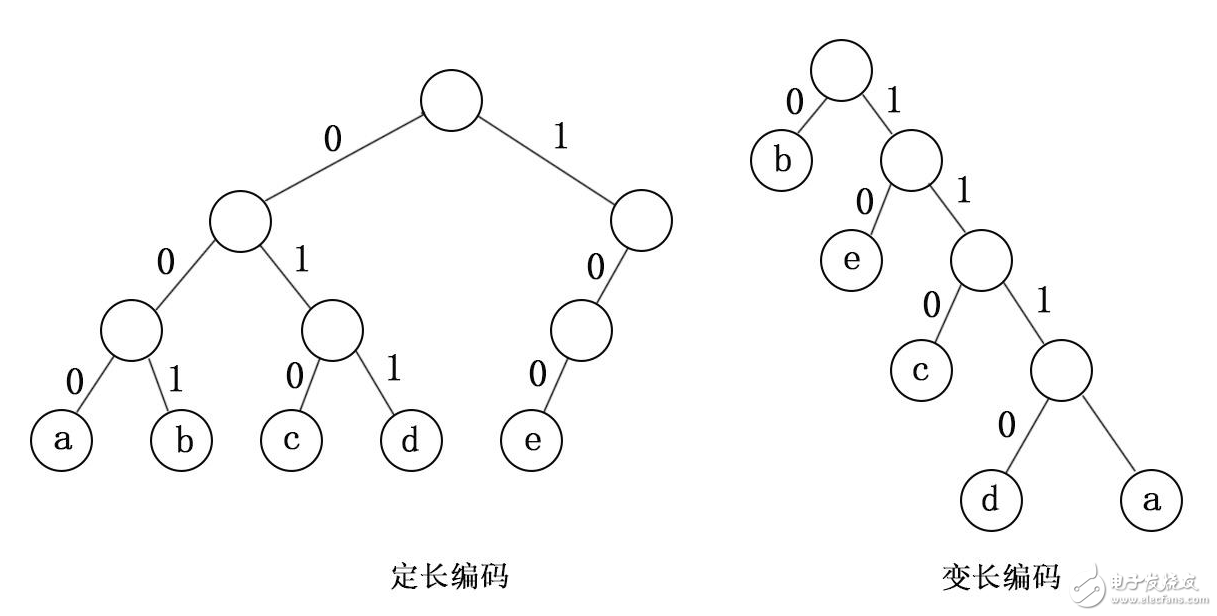
在哈夫曼树构建完成后,需要为每个字符分配唯一的编码。从根节点出发,对于每个左子树,分配编码为0,对于每个右子树,分配编码为1。经过哈夫曼树的路径,即可得到每个字符对应的编码。 - 编码与解码
根据某字符串,将每个字符替换为其对应哈夫曼编码,即可实现编码过程。而在解码时,通过从哈夫曼树的根节点开始,根据每个0或1依次向下遍历哈夫曼树,直到到达叶子节点,即可得到原始数据。
接下来,我们来详细介绍哈夫曼编码的左边是0还是1的问题。
在构建哈夫曼树时,我们需要通过贪心算法合并权重最小的两个节点。合并时,我们通常将权重较小的节点放在树的左边,而权重较大的节点放在右边。这是因为0通常表示左子树,1通常表示右子树。在递归地构建哈夫曼树时,每次合并的两个节点一定是树中权重最小的两个节点,因此,合并生成的节点通常都是左子树。而右子树则是原本树中权重次小的节点。
因此,在哈夫曼编码中,通常将左子树表示为0,右子树表示为1。这种方式可以确保每个字符的编码是唯一的,并且可以通过编码快速定位到对应的字符。
总结起来,哈夫曼编码是一种通过构建哈夫曼树实现的基于频率的变长编码方式。在构建过程中,通常将左子树表示为0,右子树表示为1。该编码方式可以高效地实现数据的压缩和解压缩,并被广泛应用于数据压缩和信息传输领域中。
-
字符
+关注
关注
0文章
234浏览量
25316 -
数据压缩
+关注
关注
0文章
31浏览量
10202 -
信息传输
+关注
关注
1文章
42浏览量
9447 -
哈夫曼编码
+关注
关注
0文章
7浏览量
2419
发布评论请先 登录
相关推荐
基于火箭动态哈夫曼编码的振动数据压缩方法
哈夫曼树基本概念与构造
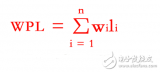
哈夫曼树的应用_哈夫曼树代码实现




 哈夫曼编码怎么算 哈夫曼编码左边是0还是1
哈夫曼编码怎么算 哈夫曼编码左边是0还是1












评论