传递函数的定义:
传递函数是一种数学工具,用于描述线性时不变系统(LTI系统)的输入与输出之间的关系,通常用H(s)表示。传递函数是Laplace变换的函数,其中s是复变量。传递函数提供了系统对不同频率的输入信号的响应的信息。
传递函数的拉氏反变换:
拉氏反变换是Laplace变换的逆变换。它将传递函数从复频域恢复到时间域。对于连续系统,拉氏反变换可以用来得到系统的单位脉冲响应或单位阶跃响应。
具体而言,传递函数的拉氏反变换可以通过以下步骤获得:
- 将传递函数H(s)转化为部分分式形式。通过因式分解,将H(s)写成多个简单的分式的和。
- 对每个简单分式进行拉氏反变换。对于H(s)中的每个项,使用拉氏反变换表格找到相应的拉氏反变换。
- 将各个项的拉氏反变换相加,得到系统的时间域响应。
下面将详细讨论拉氏变换和拉氏反变换的具体计算步骤。
首先,拉氏变换是一种数学工具,用于将时间域中的函数转换为复频域中的函数。通过拉氏变换,可以将常微分方程转化为代数方程,方便进行分析和计算。
拉氏变换的定义如下:
给定一个函数f(t)(t ≥ 0),其拉氏变换F(s)定义为:
F(s) = L{f(t)} = ∫[0,∞]e^(-st)f(t)dt
其中,s是复变量,e是自然对数的底。
拉氏变换的计算过程一般可以通过表格和性质来求解。拉氏变换具有线性性、平移性、缩放性等多种性质,这些性质可以大大简化计算过程。
对于传递函数H(s),其定义如下:
H(s) = Y(s)/X(s)
其中,Y(s)是系统的输出,X(s)是系统的输入。传递函数提供了系统对不同频率的输入信号的响应的信息。
在进行系统分析时,我们经常需要将传递函数从复频域恢复到时间域。这时,就需要使用拉氏反变换。
拉氏反变换的计算过程如下:
- 将传递函数H(s)转化为部分分式形式。通过因式分解,将H(s)写成多个简单的分式的和。如果H(s)中存在重复的极点或有理因子,就要将其部分分式展开为简单分式。
- 对每个简单分式进行拉氏反变换。对于H(s)中的每个项,使用拉氏反变换表格找到相应的拉氏反变换。
- 将各个项的拉氏反变换相加,得到系统的时间域响应。在求和时,注意考虑每个项的幂次和重数的影响。
通过拉氏反变换,可以得到系统的单位脉冲响应或单位阶跃响应。这些响应函数提供了系统在时间域中的输出信息,可以用来分析系统的动态特性。
总结起来,传递函数是一种描述系统输入与输出之间关系的数学工具,通过拉氏反变换可以将传递函数从复频域恢复到时间域。拉氏反变换的计算过程包括将传递函数转化为部分分式形式,对每个简单分式进行拉氏反变换,将各项响应函数相加。拉氏反变换提供了系统在时间域中的响应函数,可以用来分析系统的时域特性。
-
传递函数
+关注
关注
0文章
102浏览量
13943 -
输入信号
+关注
关注
0文章
455浏览量
12547 -
LTI系统
+关注
关注
0文章
5浏览量
5685
发布评论请先 登录
相关推荐
开环传递函数是怎样影响系统的?
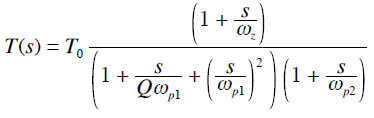
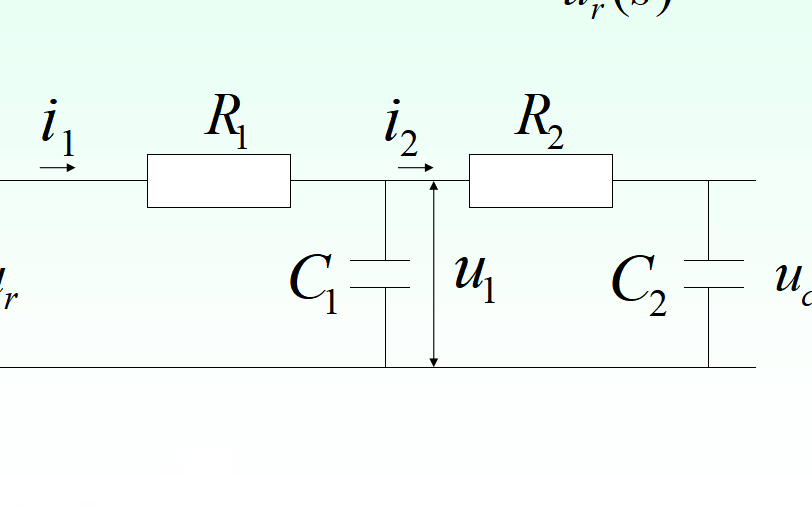
传递函数拉氏变换在电路分析中的应用
基于Butterworth标准传递函数设计
传递函数极点和零点的影响是什么
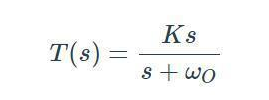
传递函数是怎么定义的以及如何写出传递函数?
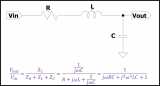
传递函数的频率特性




 传递函数的定义是什么 传递函数的拉氏反变换是什么响应
传递函数的定义是什么 传递函数的拉氏反变换是什么响应
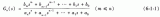










评论