如何求耦合电感并联的等效电感

求解耦合电感并联的等效电感的方法有多种，下面将解释两种方法：直接相加法和矩阵法。

1. 直接相加法：
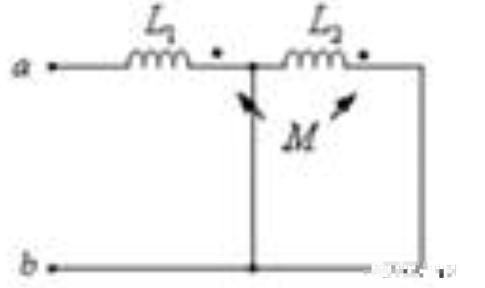
   耦合电感并联的等效电感值可以通过将每个独立的电感相加得到。假设有两个电感L1和L2并联，它们之间存在耦合系数k。则它们的等效电感可以表示为L12。
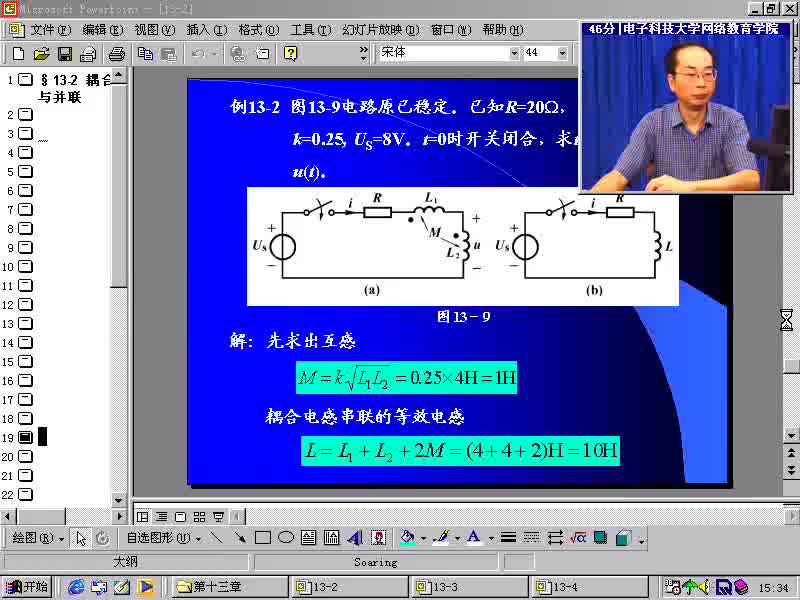
   L12 = L1 + L2 + 2M
   其中，M表示耦合电感，根据定义，有M = k √(L1 • L2)。
   因此，L12 = L1 + L2 + 2k √(L1 • L2)。
   这就是直接相加法。
2. 矩阵法：
   矩阵法是一种比较复杂的方法，但它可以方便地求得多个电感并联的等效电感，特别是在有多个电感或者复杂电路中应用较多。以下是具体步骤：

a) 构造阻抗矩阵：
首先，将每个电感表示为一个阻抗元素。对于每个电感Li，可以通过Li = jωLi进行表示，其中j是虚数单位，ω是角频率。然后，将这些阻抗元素构建成一个n×n的矩阵，其中n是并联电感的个数。这个矩阵被称为阻抗矩阵Z。

b) 耦合系数矩阵：
然后，构造一个n×n的耦合系数矩阵K，其中Kij表示电感Li和Lj之间的耦合系数。如果电感Li和Lj之间没有耦合，则Kij等于0。如果它们之间有耦合，则根据具体情况确定耦合系数的值。

c) 等效电感矩阵：
接下来，计算等效电感矩阵L。等效电感矩阵L可以通过下式计算得到：
L = (Z^-1 - K)⁻¹
其中Z^-1是阻抗矩阵Z的逆矩阵。

d) 等效电感：
最后，等效电感是等效电感矩阵的主对角线上元素的和，即L12 = L11 + L22 + ... + Lnn。

通过上述步骤，可以求解耦合电感并联的等效电感。这种方法可以应用于多个电感的情况，并且具有较高的求解精度。

综上所述，可以看出，求解耦合电感并联的等效电感的方法有直接相加法和矩阵法。直接相加法较为简单，适用于只有少量电感的情况。而矩阵法比较复杂，但适用于有多个电感或复杂电路的情况，具有较高的求解精度。