频率滤波的原理、傅立叶变换与频域滤波以及滤波应用介绍

本文简单介绍了频率滤波的原理、傅立叶变换与频域滤波以及滤波应用。

干涉图是光学实验中常见的现象，它反映了光波相互叠加形成的干涉条纹，展现了光的波动性质。在干涉图的处理和分析中，频率滤波起着至关重要的作用。让我们一起深入探讨干涉图滤波的奥秘吧！

为了增强干涉图图像，减少外界因素对干涉仪干涉现象（由两个或多个受控波前产生的干扰）引起的噪声，采用低通技术作为预处理滤波步骤。干涉图平滑和去噪是低通滤波器在干涉测量中应用的主要目的。滤波技术可以分为空间域或频域，其中A空间滤波直接应用于干涉图图像，像素到像素，而B频率滤波通常在傅里叶域中执行。带通和带阻是一些可以应用于傅里叶域的滤波技术，这些滤波器用于衰减特定噪声的某些频率。

频率滤波原理与方法

频率滤波的原理是通过将图像的频域表示与某种滤波函数进行卷积操作，以实现对特定频率成分的调整或抑制。常见的频率滤波包括低通滤波、高通滤波、带通滤波和带阻滤波。例如，低通滤波可用于去除图像中的高频噪声，而高通滤波则可增强图像的边缘特征。

图 1. 空间低通滤波器：(a) 原始 ronchigram，(b) 采用高斯、二次、三角函数和平均掩码，以及 3*3、5*5 和 7*7 卷积掩码大小。

傅立叶变换与频域滤波

干涉图的频域滤波通常是在傅立叶域进行的。傅立叶变换可以将图像从空间域转换到频率域，从而使得频率信息更加清晰可见。通过对傅立叶变换后的频谱进行滤波操作，可以实现对干涉图的精确处理和优化。频域滤波通常在傅里叶域中进行。傅里叶变换反映了从空间到频域的变化。方程（1）和方程（2）表示一对二维离散傅里叶变换。

方程（1）

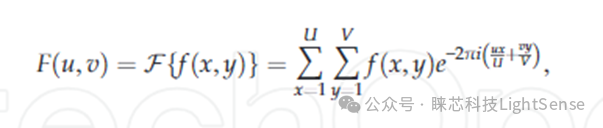
方程（2）

 

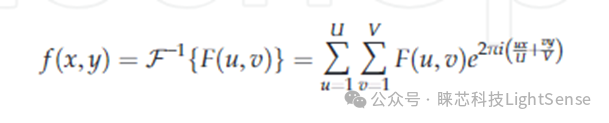
其中 (u, v)是频率坐标，U、V是图像大小（以像素为单位），F 和 F −1分别是傅里叶变换和傅里叶逆变换算子。

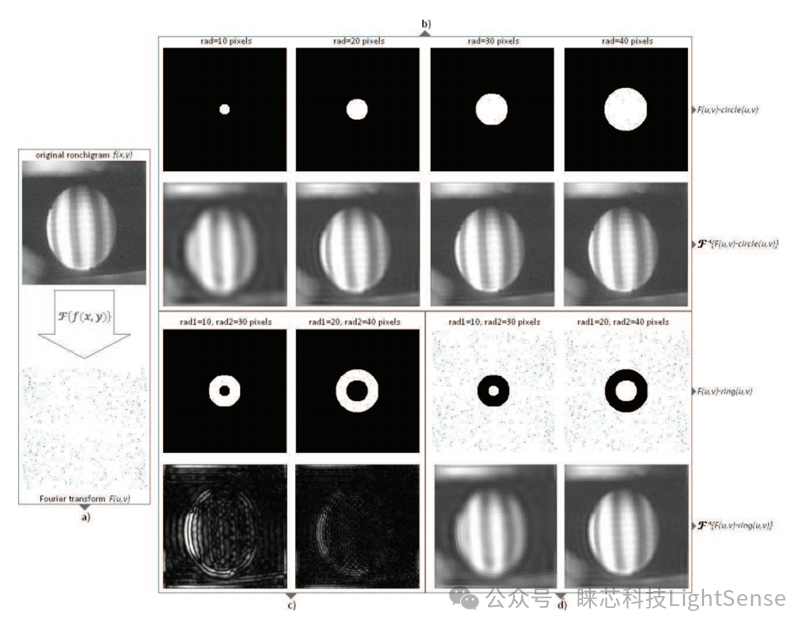
图 2. 频域滤波：(a) 原始 ronchigram 的傅立叶变换，(b) 不同半径的低通滤波的二进制圆掩模，（c）具有两种尺寸的二进制圆掩模的带通滤波，以及（d）具有两种尺寸的带阻滤波二元环掩模。

滤波应用与效果展示

在实际应用中，频率滤波在干涉图的处理中发挥着重要作用。通过不同类型的滤波操作，我们可以调整干涉图的清晰度、对比度和细节等方面，从而获得更加清晰和准确的图像信息。本文结合实例展示了低通、带通和带阻滤波在干涉图处理中的效果，如图2所示。

结语

频率滤波是干涉图处理中的一项重要技术，它不仅可以优化干涉图的质量，还可以提高图像的可读性和分析性。通过深入学习和掌握频率滤波的原理和方法，我们可以更好地理解和利用干涉图，为光学研究和实验提供更多可能性。

审核编辑：刘清