这是多相网络发明者Gingell的发明专利。多相网络在单边带(SSB)发射机中应用频繁,由于这种多相网络可以提供宽频移相,而且特别经济且结构简单,近年来在IQ调制器中逐渐得到重视,这种网络非常有趣。看起来似乎是一种非平面网络。
POLYPHASE SYMMETRICAL NETWORK
对称多相网络
US 3,559,042
Michael John Gingell, Sawbridgeworth, England, assignor to International Standard Electric Corporation, New York, N.Y., a corporation of Delaware
Filed May 19, 1969, Ser. No. 825,871
Claims priority, application Great Britain, June 7, 1968,
Int. CI. G05f
1. 摘要
本文披露了对称的多相网络,该网络至少包括一个多相网络部分,其中包括个单相网络电路,每一个电路都有一个第一阻抗,它连接在与该电路相关的输入和输出端子之间。每一个网络电路的输入端子也通过一个与第一阻抗有不同相位特性的第二阻抗与其相邻相位(超前或滞后)的输入信号的电路的输出端子连接。当提供两个或多个网络时,它们会级联连接。
2. 发明背景
该发明涉及多相网络,更具体地说是对称的多相网络。
3. 总结
本发明的特点是提供了一个对称的多相网络,该多相网络包括至少一个多相网络,其中每个多相网络包括N个单相电路,其中N是大于1的整数;每个电路都有一个输入端,一个输出端,在电路的输入和输出端之间耦合了一个第一阻抗,其具有给定的相位角特性;在电路的输入端和另一个电路的输出端之间耦合了第二阻抗,其相位角特性与给定的相位角特性不同,该第二阻抗响应于输入信号的相位,该输入信号的相位与该电路响应的输入信号的相位相邻。
4. 首选实施例的描述
为了理解根据本发明的对称多相网络的工作原理,必须引入负频率的概念。考虑一个四相系统,如图 1(A) 所示,其四个输入端子上分别施加有,的电压,那么输入信号可以被称为对称的,因为所有的电压在幅度上都是相等的,并且每两个之间相隔。例如,按照正序,依据惯例,所有的矢量都是逆时针旋转的,并且路径1上的电压超前于路径2上的电压。同样,路径2上的电压超前于路径3上的电压,等等。如果现在矢量旋转方向相反,即如图 1(B) 所示,系统仍然是对称的,但是负序,因为路径1上的电压滞后于路径2上的电压,而不是像之前那样超前。
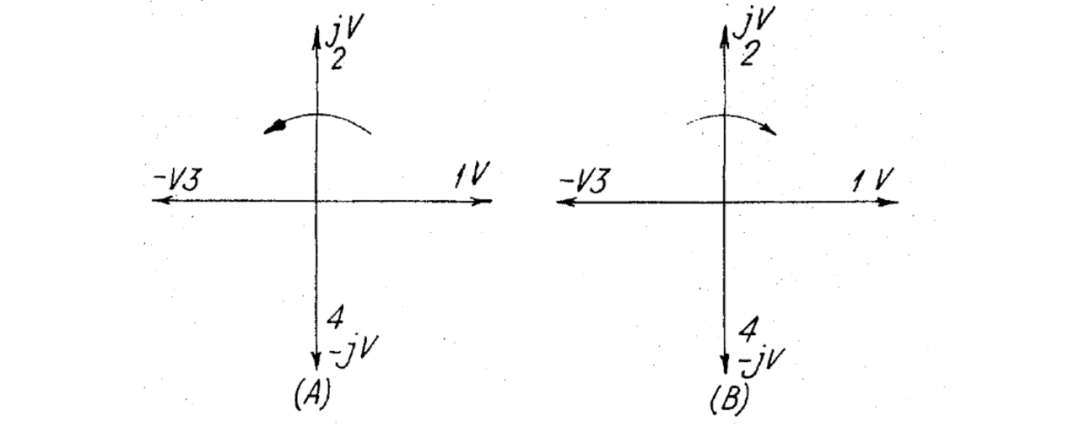
图 1(A) 和 1(B) 分别显示了正和负序(正和负频率)的四相矢量图;
考虑路径上的电压,从图 2 可以看出,
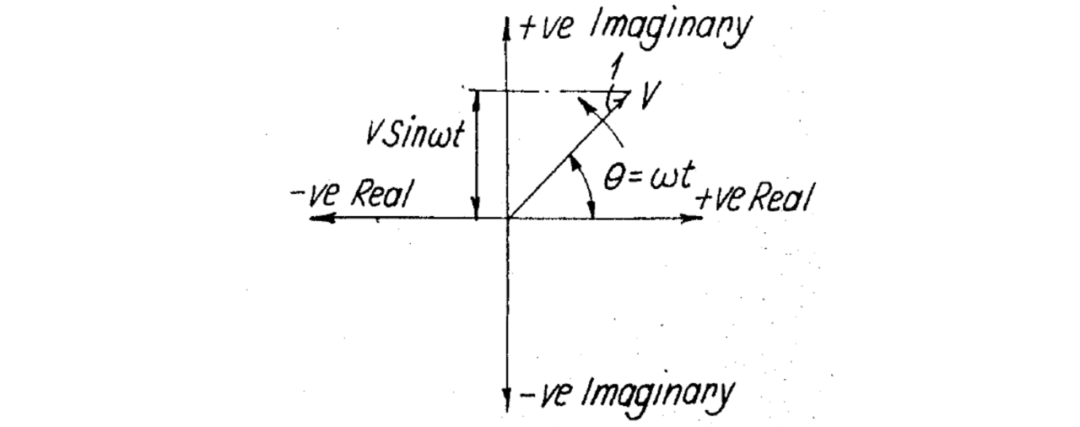
图 2 示出了正序的四相矢量图;
这个电压是,即当它逆时针旋转时,矢量1在虚轴上的投影。当矢量的顺序被反转时,将会观察到。因为
可以说,在一个单相电路上,正序列代表正,负序列代表负。因此,当以下文中提及单相网络的特性时,提到正和负频率,它指的是分别在包含个单相网络的多相网络中的正和负序列。
众所周知,在该领域中,可以构建无源RC全通网络,并可以构造两个这样的网络,它们的输出之间的相位差约为,带宽由网络复杂度决定。
根据本发明的对称多相网络,其功能与两个单独的网络完全相同,并且对元件公差的敏感性要小得多,至少包括图 3A 所示的类型的一个网络。当提供多个这些网络时,它们会级联连接。
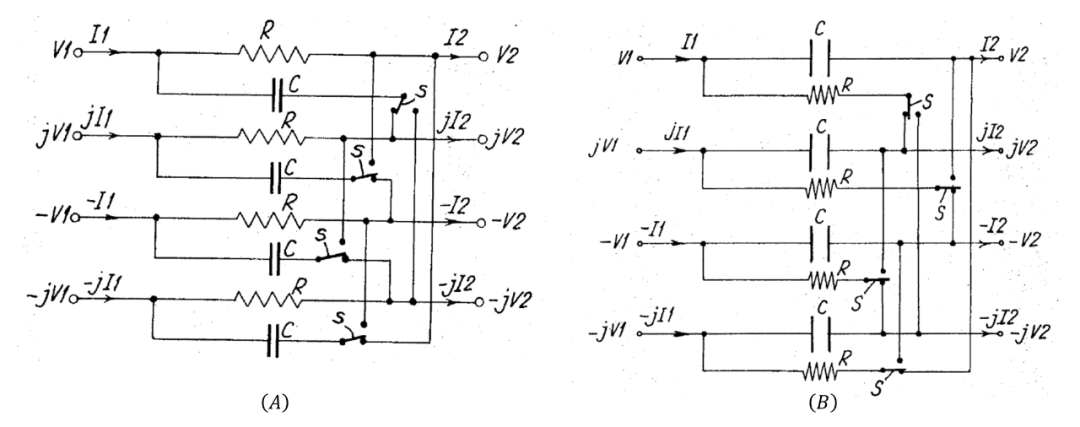
图 3A 和 3B 示出了根据本发明的对称四相网络的两个电路图;
参考图 3A,其中显示了一个四相网络段以及与每个相关联的典型电压和电流,并且每个相位(单相电路)都包括一个与其相关的相位的输入和输出端子之间的电阻。当开关处于图示位置时,每个单相电路的输入都通过电容连接到响应输入信号相邻的超前相位的单相电路的输出。
该四相网络段的每个相的链矩阵为:
通过这个矩阵,从中可以看到传输零点为:
对于单相而言,插入损耗采用图 4 中由点划线 5 所示的形式表示。
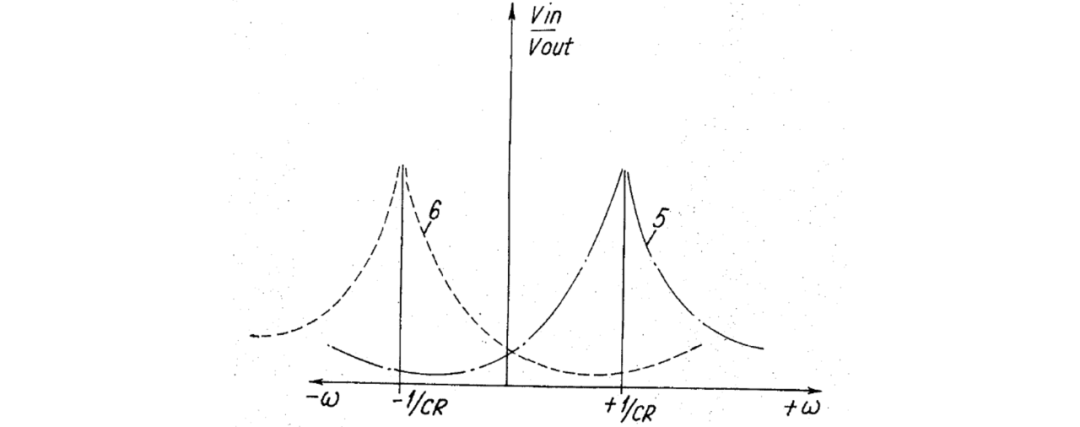
图 4 展示图 3 中所示网络的衰减特性;
应当指出,当开关S移至其另一位置时,网络根据图3A的每个相的输入可以通过电容器连接到响应输入信号相邻滞后相的单相电路的输出,而不是响应输入信号相邻超前相的单相电路的输出。在这种情况下,方程1的链矩阵将变为:
因此,从这个方程可以看出,传输零点会出现在
并且单相电路的插入损耗将采用图 4 中由虚线 6 所示的形式。
在前面所述的每个对称多相网络段中,电容C和电阻R可以互换,如图3B所示。这种互换导致在零频率处的衰减特性反转,并通过网络段引入的相位偏移。例如,对于图3A中的网络段,当电容和电阻被交换时,方程1的链矩阵变为:
对于某些应用,单网络段的特性可能不是非常理想,在这些应用中需要能够将衰减特性调节到所需的形式。例如,可能需要图 5中所示的衰减特性,
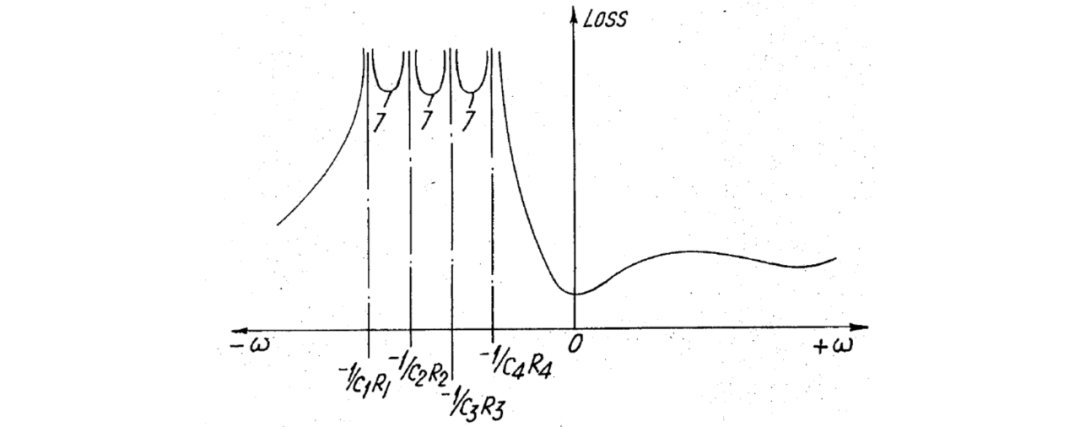
图 5 示出了包括四个如图3所示类型的网络以级联方式连接的对称多相网络的衰减特性;
在这种情况下,需要提供四个串联连接的网络级联,传输零点 6 在下边带出现在:
和
并且每个都与四相中的一个相位关联。
每个网络段相关电路元件的总值确定了与该特定网络段相关的传输零点的位置,并且可以通过在保持这些元件的总值的同时,使任何一个网络段相关电路元件的值产生变化,来改变图 5中所示衰减特性中通带部分的形式。通过这种方式,通带的平均衰减值可以根据特定要求进行变化。当然,传输零点之间的衰减特性之间的最小值(即图 5中所示的值7)也会相应变化,从而导致衰减特性中阻带部分的平均衰减值的变化。
可用于确定多个级联网络段特性的综合方法涉及将这些段的矩阵相乘,以确定元件的总体传递函数,即与每个网络段相关的电阻和电容。然后,将级联网络段的传递函数加上四象限调制等于等效两个全通网络的传递函数加上四象限调制。
通过使的幂的系数相等,可以确定对称多相网络的元件值,并获得所需的特性。
利用这种综合过程,可以很容易地设计具有多达四个串联网络部分的对称多相网络。超过四个部分后,代数计算开始变得复杂,尽管从理论上看,网络复杂性没有限制。鉴于这个问题,人们发现使用计算机来确定各个网络部分的元件值是有利的,这些元件值给出了所需的插入损耗特性。
四相以外的对称多相网络稍微复杂一些。三相网络段的电路图作为示例在图 6A中给出。这种三相网络段可用来为电动机提供三相50 Hz电源,基本上与图3A中的网络段相同,只是各相的电压不同,并且当开关S1处于图示位置时,电阻与电容串联接在每个相的输入与响应输入信号相邻超前相的单相电路的输出之间。应当指出的是,前文对图3A和3B电路图的修改也适用于此电路结构。注意图 6B中元件的交换以及开关S1移动到其另一个位置将每个相的输入连接到响应相邻滞后相的单相电路的输出。
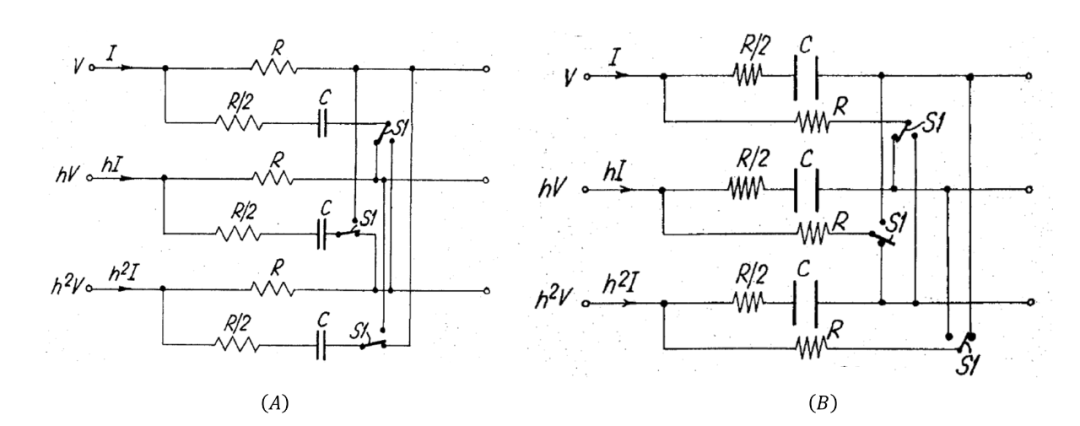
图 6A 和 6B 示出了根据本发明的对称三相网络的两个电路图;
每个相的电压分别是 和,其中并且另外根据本发明的对称多相网络的主要要求是,每个网络部分必须在每个相位之间的输入和输出端之间包括第一阻抗,且每个相位的输入必须通过具有与第一阻抗不同的相角特性的另一阻抗连接到相邻的相位,即超前或滞后。
前面段落中概述的无源对称多相网络由于其无源性而受到限制,其传输函数的传输极点位于其平面零极点图的虚轴上,而传输零点位于此图的实轴上,如图 7所示。
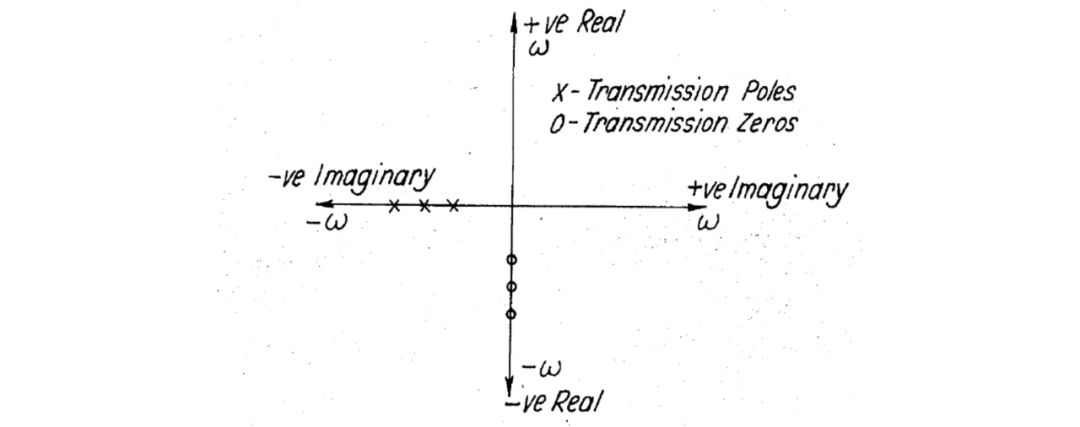
图 7 展示了根据本发明的无源对称多相网络的平面零极点图;
对于某些类型的函数,传输极点通常不在虚轴上。实现此类函数方法是在网络部分的串联中插入-相1到的阻抗变压器,如在审专利中所述,Ser. No. 826,149,于1969年5月20日提交(M. J. Gingell-9),例如,在图 8中,其中一个四相1到阻抗变压器被插入在图3中所示的两个四相网络之间。
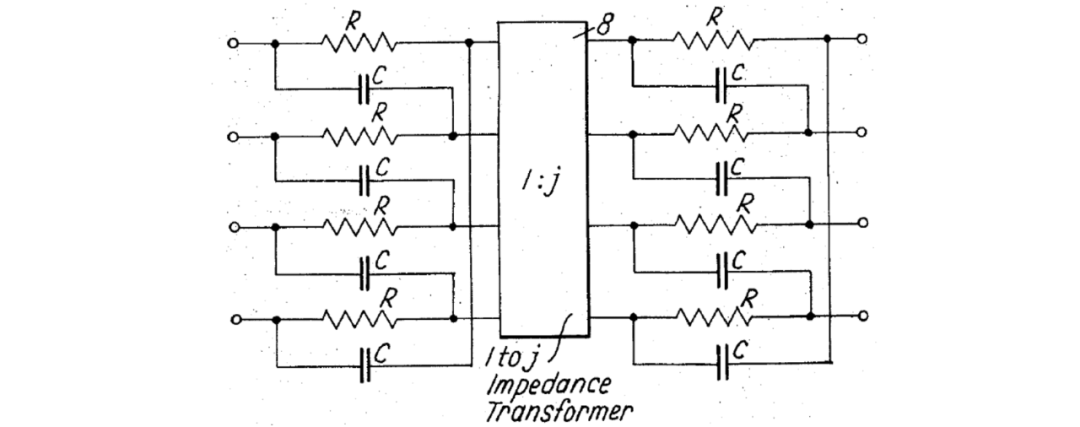
图 8 示出了根据图3的对称四相网络的两个电路图,通过四相1到j阻抗变压器以级联方式连接;
除了在每个网络段的每个相和N相1到j阻抗变压器的相应相之间插入N相1到j阻抗变压器之外,还可以使用负阻抗转换器(impedance converters)或逆变器(inverters)来获得极点位置的进一步自由度。
前文所述的对称多相网络在英国专利号1,098,250中所述的N路频率转换系统中具有特定但不一定是专有的应用,并且以类似于传统正交调制但优于传统正交调制的方式进行单边带生成。
-路频率转换系统(N-path frequency translation system)的传递函数由以下公式定义:
其中 是一个常数 是 路中网络的传递函数 是输入开关频率 是输出开关频率
译注:N-path滤波器的概念可以追溯到上世纪40年代,它是一种利用多路径切换系统来实现射频信号滤波的技术。虽然具体的发明者信息不容易在现有资源中找到,但在国际固态电路会议(International Solid-State Circuits Conference, ISSCC)上,Bram Nauta教授曾解释了N-path滤波器的基本概念及一些示例。这表明在学术和工业界,N-path滤波器技术已经得到了广泛的讨论和应用。
从历史的发展来看,N-path滤波器的产生与无线通信技术的进步密切相关。最初的无线通信技术主要依赖于模拟波调制技术,随着时间的推移,数字调制技术逐渐得到应用,为信息传输提供了更为高效的解决方案。
N-path滤波器技术在近年来得到了相当多的关注,因为它们具有许多有趣的特点,如高Q值、高线性和低损耗等。它们可以作为锐截止滤波器,替代大型的声表面波(SAW)滤波器,并在直接转换接收器中用作混频器。这种技术的出现和发展,为射频信号处理提供了新的、更为紧凑和高效的解决方案。
N-path filter技术类似于使用ADC采样信号,然后通过数字并行处理滤波,然后又拼回给到DAC输出,不过这里N-path filter完全是模拟信号的处理,而没有变为数字,所以N-path filter的效率更加高效。
https://link.springer.com/article/10.1007/s10470-018-1170-0#:~:text=N,mixers%20in%20the%20direct
可以看到,传递函数 沿实频率轴移动了。通常,在 的 路滤波器(N path filter)系统中,这将导致一个关于频率 对称的带通特性。如果在 路中连接了低通滤波器,结果特性将是一个移位的低通滤波器(包括负频率的,它是正频率的镜像)。这在图 9(A) 和 (B) 中所示。
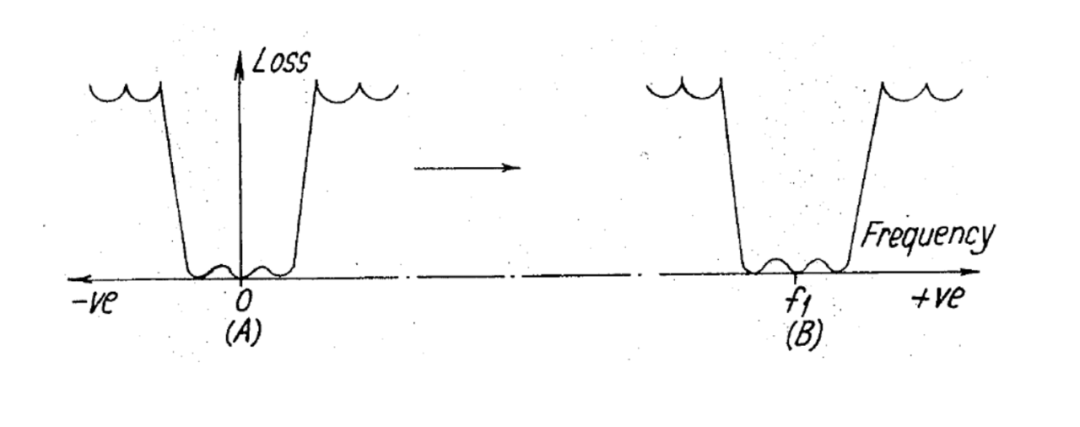
图 9(A) 和 (B) 示出了具有低通滤波器连接在其每个N路中的N路频率转换系统的频率响应曲线;
当涉及调制过程时,对称特性通常非常浪费。在这种情况下,通带的一侧需要的衰减远远大于另一侧。通过使用本发明的对称多相网络,特性可以更有效地适应需求。此外,不需要开关或载波频率也不再需要在中频处。图 10(A) 和 (B) 以示例的方式说明了这一点。
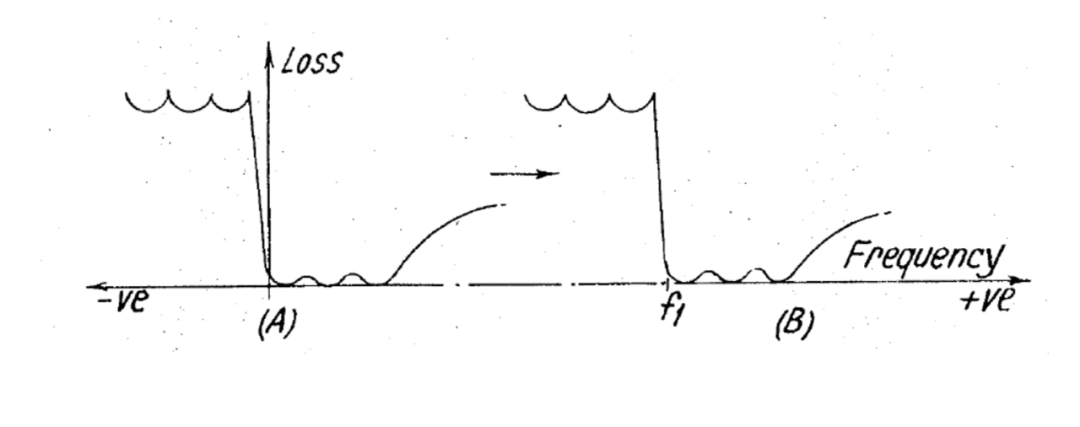
图 10(A) 和 (B) 示出了使用本发明的对称多相网络的N路频率转换系统的频率响应曲线;
根据本发明的对称多相网络也可用于将单相分割为 相。
根据对称分量理论,任何不平衡的 向量系统都可以表示为 对称向量系统之和。例如,如果考虑一个具有在一个相位上的 输入的两相(正交)系统,那么这相当于同时应用两个相反序列的两相信号,如图 11(A) 到 (C) 所示。如果系统的传递函数对应于图 11(B) 的向量系统是,那么对应于图 11(C) 的向量系统将是。图 12 显示了一个只在一个相位上有输入的两相系统,其中包括一个两相网络 12,其一个相位的输入 连接到电压源,另一个相位的输入 连接到地电位,即。相位1的电压输出 通过调制器9和求和单元11连接到输出,相位2的电压输出 通过调制器 和求和单元 连接到输出。
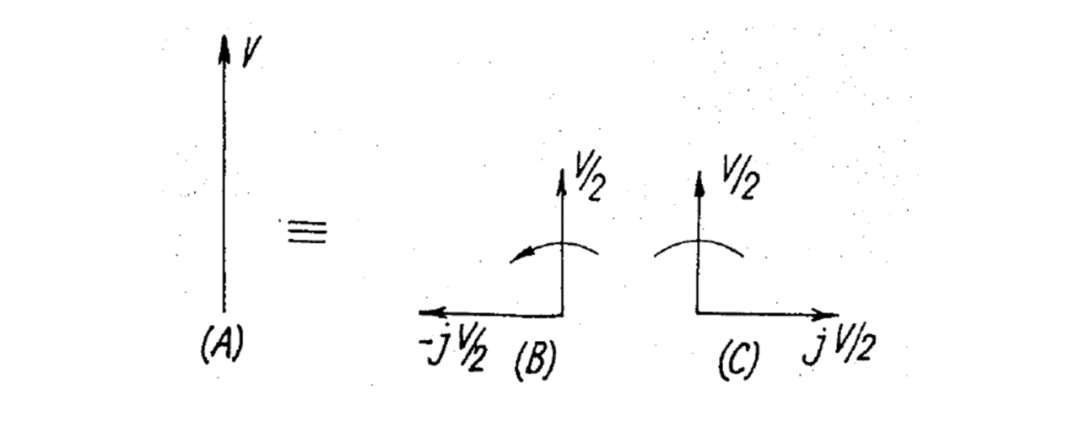
图 11(A) 到 (C) 展示了矢量图;
因此,在相位1的输出上,
在相位2上
如果然后对 和 应用正交调制,如图 12 所示,结果输出为
效果就好像首先进行了调制,然后是正常类型的滤波器,其响应为
为此目的,多相网络的特性将如图 10 所示。然后,下边带将被抑制,而上边带
将被通过。应该注意,根据本发明的网络的两相版本在实际形式中不能实现,但这种基本方法可以用于任意数量的相位,并且因此可以用于根据本发明的对称多相网络。
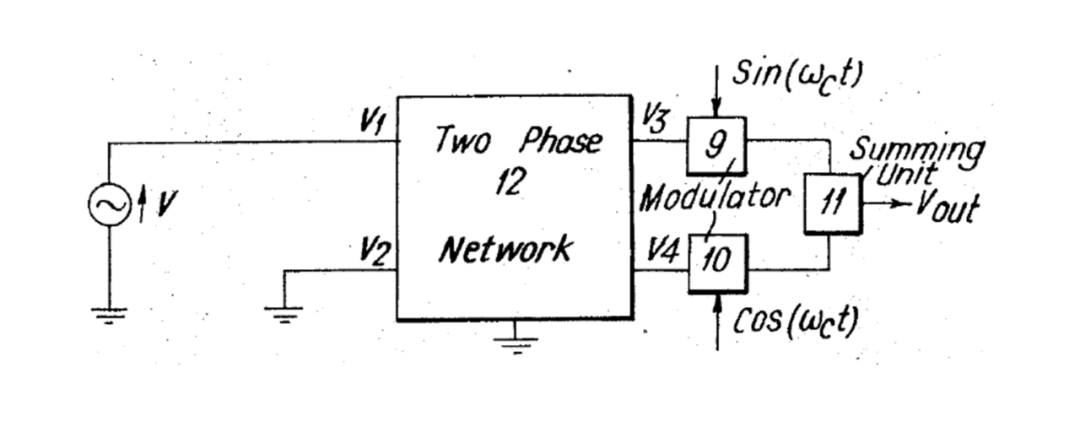
图 12 展示了一个两相正交调制器网络的电路图。
还应该注意,可以不使用调制器而使用图 12 的网络,从而简单地作为一个电路,从单相输入提供两相输出。只要网络为负序列输入提供足够的衰减并通过正序列输入。图 11 显示了一个合适的特性。以类似的方式,可以从单相输入生成一个-相输出。
审核编辑:黄飞
-
变压器
+关注
关注
159文章
7462浏览量
135134 -
电容器
+关注
关注
64文章
6217浏览量
99534 -
滤波器
+关注
关注
161文章
7795浏览量
177992 -
电压
+关注
关注
45文章
5598浏览量
115701 -
RC网络
+关注
关注
0文章
11浏览量
7318
原文标题:对称多相网络
文章出处:【微信号:电路设计小工具,微信公众号:电路设计小工具】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
对称多处理 (SMP) 的应用优势
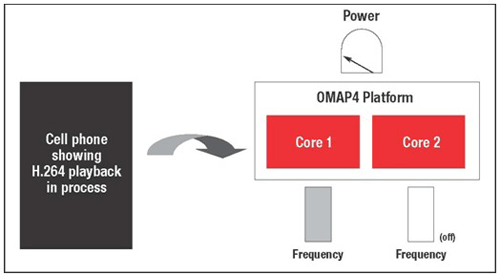
SMP(对称多处理)系统
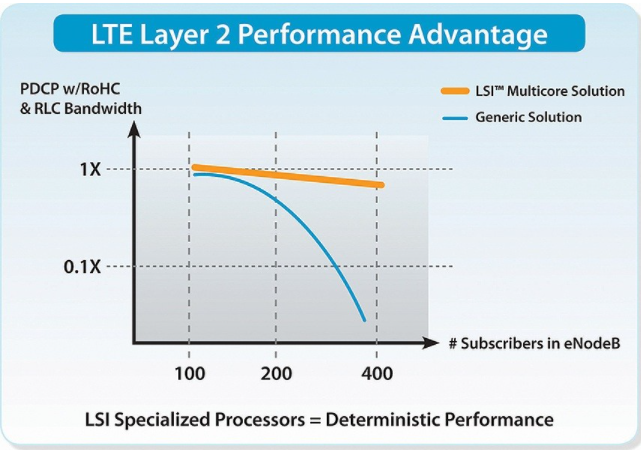
LSI丰富非对称多核解决方案
LSI推出最新系列非对称多核芯片解决方案和软件
裸机AMP(非对称多进程处理模式)





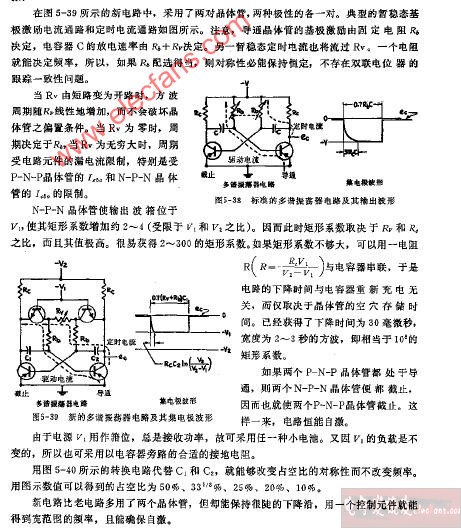
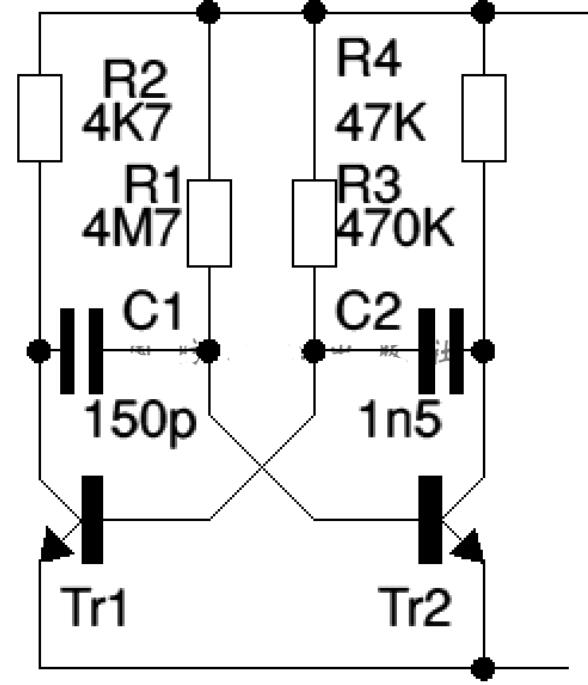
 对称多相网络的工作原理
对称多相网络的工作原理











评论