聊一聊啥是“阻抗修正”去嵌入技术

在非标准接口器件测试中，使用去嵌入方法消除测试夹具等对测试结果的影响已经被很多小伙伴们熟知。

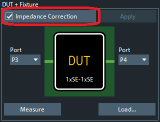
细心的小伙伴们可能注意到了，在“Deembed Assistant（去嵌助手）”中有个“Impedance Correction（阻抗修正）”的选项。小编接到过很多小伙伴的相关提问。关于这个问题，帮助和手册中都没有详细的说明，也挺难用一两句话说明白的。今天我们就来聊一聊啥是“阻抗修正”去嵌入。

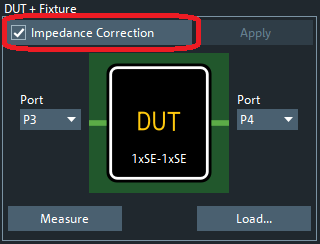
图 1“ImpedanceCorrection（阻抗修正）”选项

我们以最常见的单端（Single End）“2x-Thru”去嵌方式来说明。

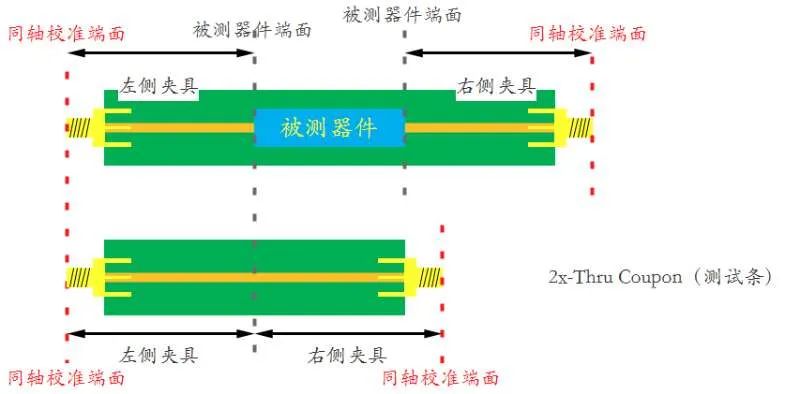
图 2“2x-Thru”去嵌方式

熟悉去嵌操作的小伙伴都知道，我们只需要测量一次“2x-Thru Coupon（测试条）”，再测试一下“夹具-被测器件-夹具”，R&S的矢网就可以显示被测器件的S参数结果（去嵌后的结果）。那我们就来看看，R&S的矢网背着我们干了哪些“好事”！

第一步，R&S的矢网在测量得到“2x-Thru Coupon（测试条）”的S参数以后，要分别解出“左侧夹具”和“右侧夹具”。每侧的夹具都用一个s2p文件来表征。这一步实际是整个去嵌入的关键。

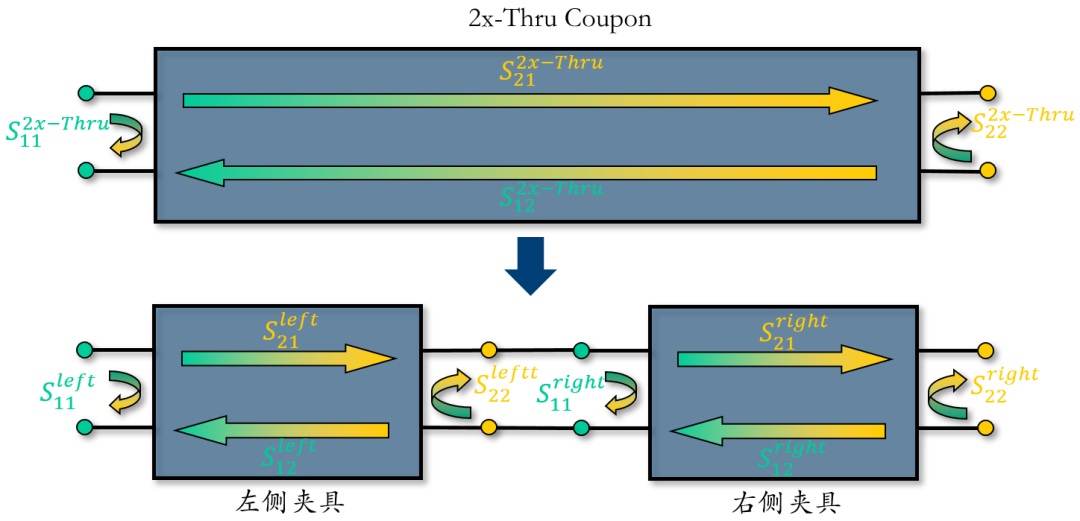
图 3由“2x-Thru Coupon（测试条）”测试结果解出“左侧夹具”和“右侧夹具”

为了完成这一步，

我们需要引入两个假设：

假设Ⅰ：“左侧夹具”和“右侧夹具”是完全镜像的

这一假设实际上也是个选项：

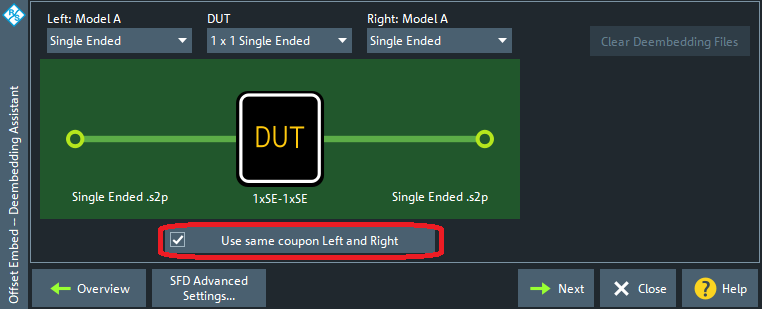
图4对称夹具选项

如果不勾选这个选项，则需要两个“2x-Thru Coupon（测试条）”，这个操作我们以后再说。

根据这一假设，我们有：

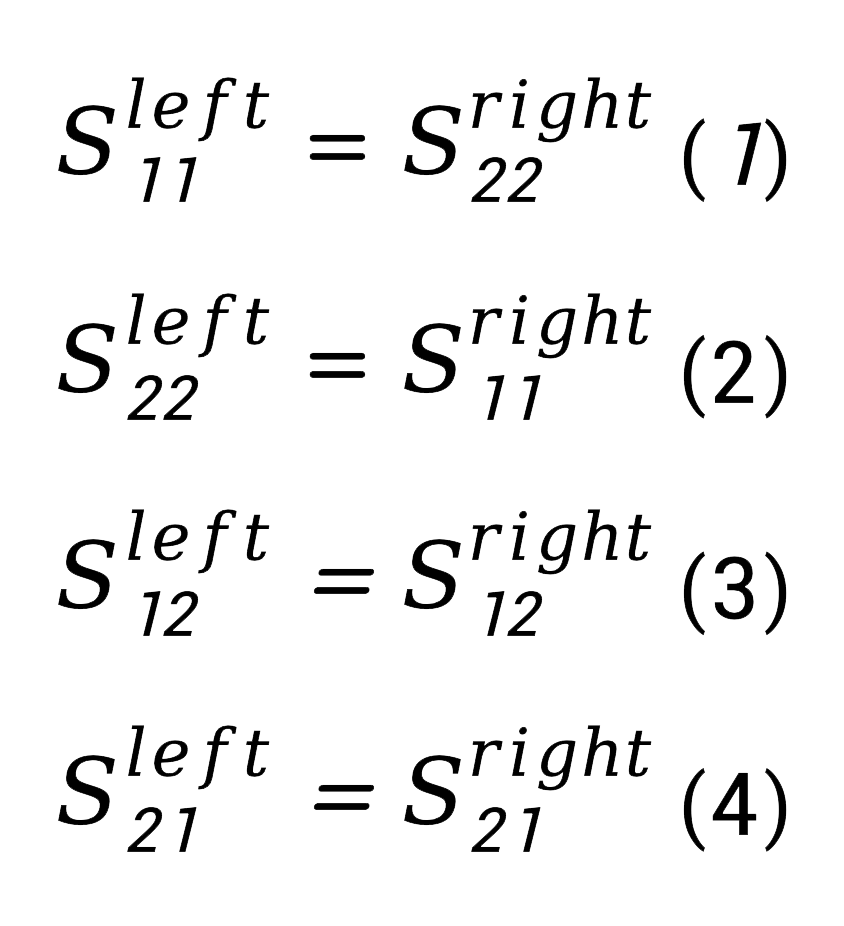
假设Ⅱ：“左侧夹具”和“右侧夹具”都是互易的即：

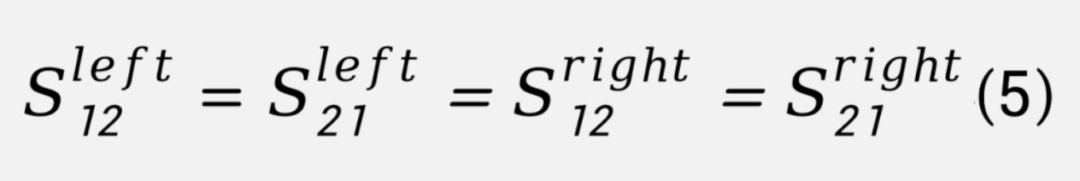
这个假设对于这样的无源夹

具是合理的。

所以我们一共有三个未知数：

现在我们来看看我们手里的已知量，虽然我们测量得到了“2x-Thru Coupon（测试条）”的四个S参数，但由于我们假设“左侧夹具”和“右侧夹具”是完全镜像的。所以有：

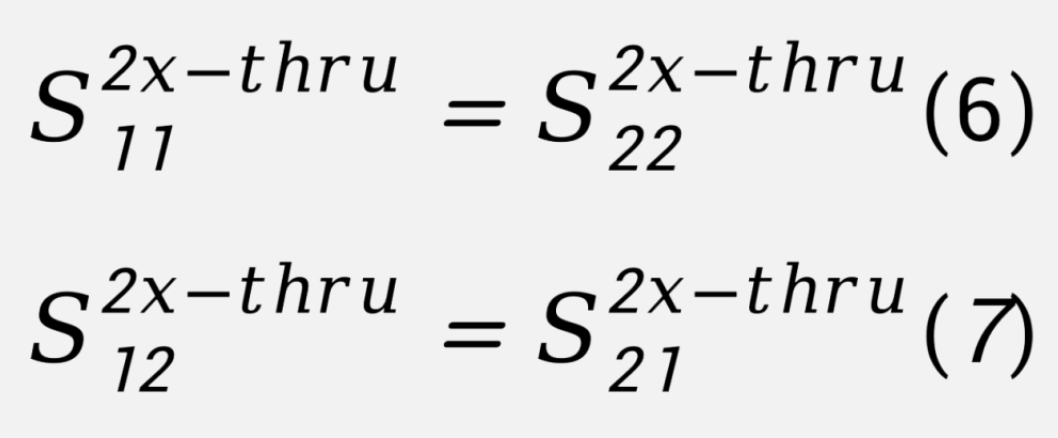
因此，我们可以用的已知量只有两个：

利用S参数级联公式或者信号流程图，

我们可以推导出：

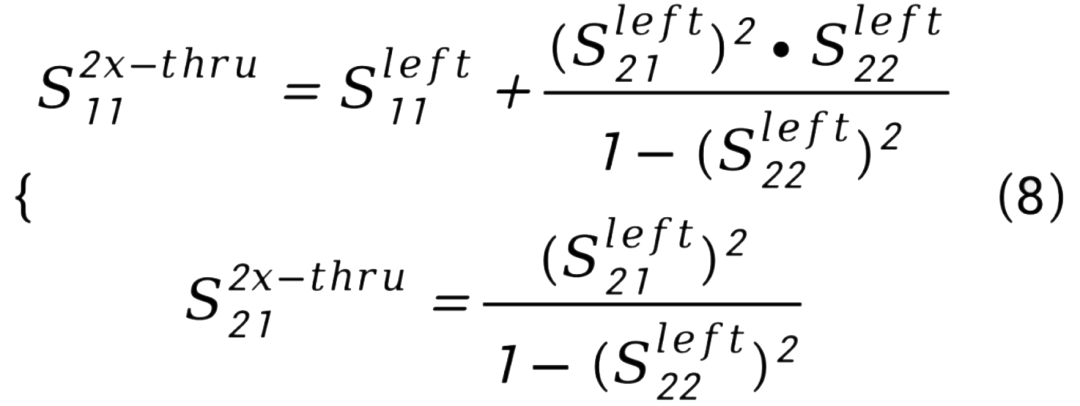
两个方程，三个未知量，我们是解不出来唯一解的，看来我们陷入了困境。幸亏祖师爷之一的傅里叶老先生提供了一个神器：傅里叶变换与逆变换！既然频域解决不了，我们就转到时域去！矢量网络分析仪的时域测量可以参考我们之前的文章《【实践分享】网分的TDR功能，时频域的双向奔赴》。

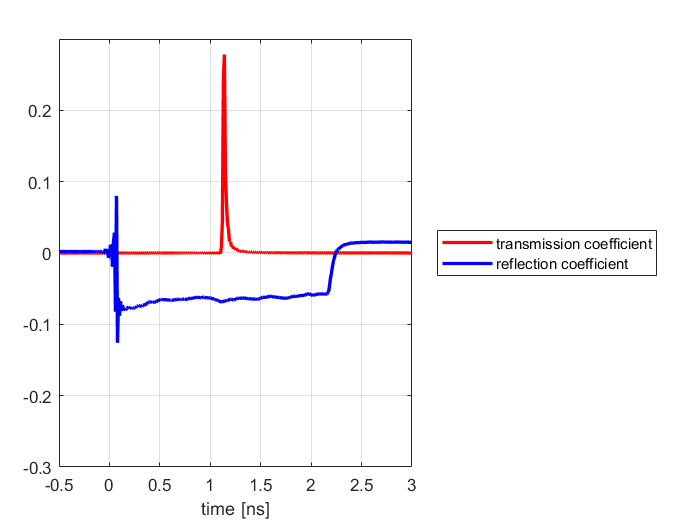
图5“2x-Thru Coupon（测试条）”时域结果

我们把

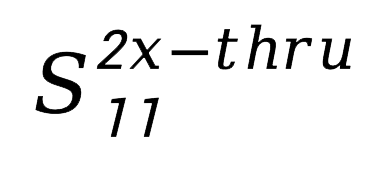
的结果变换到时域（阶跃响应），得到图 5中蓝色迹线；再把

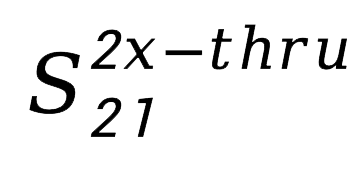
的结果变换到时域（冲激响应），得到图 5中红色迹线。显然，传输的时间是反射时间的一半，也就是说红色迹线峰值对应的位置就是“2x-Thru Coupon（测试条）”的中点，也就是“左侧夹具”和“右侧夹具”的分界面。然后，我们祭出另一样法宝：时域门（Time Gate）！大刀一挥，把

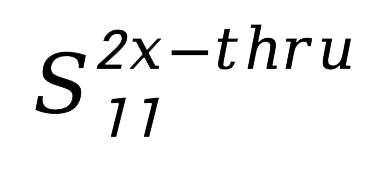
的时域阶跃响应一刀两断（Gating），就得到了

的时域阶跃响应（图 6）。

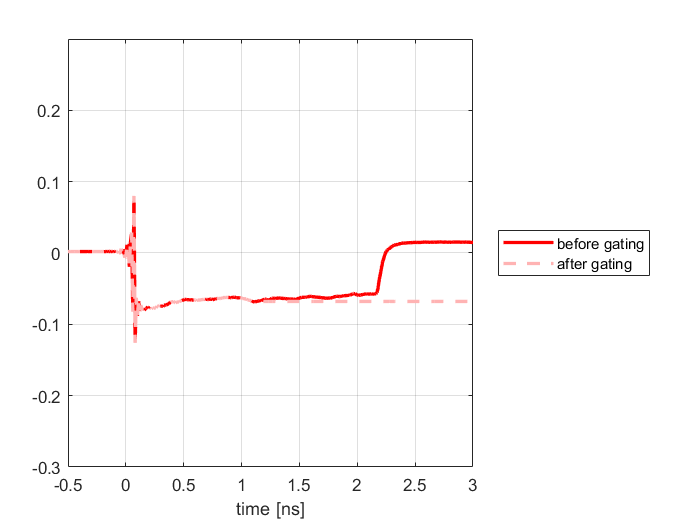
图6利用时域门，把

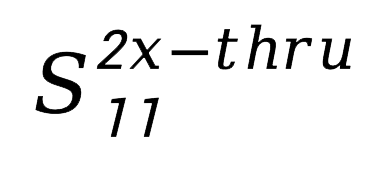
变成

有了

的时域阶跃响应结果，利用傅里叶变换，

的频域结果自然唾手可得。惊不惊喜？意不意外？现在，式（8）中有两个方程，两个未知数，我们可以得到“左侧夹具”的s2p文件了。自然，“右侧夹具”的s2p文件也就得到了。剩下的事情就简单了：利用“左侧夹具”和“右侧夹具”的s2p文件，以及测得的“夹具-被测器件-夹具”s2p结果，就可以计算出“被测器件”的s2p结果了。

当然这里还隐含了一个假设：

假设Ⅲ：“夹具-被测器件-夹具”和“2x-Thru Coupon（测试条）”里的“左侧夹具”和“右侧夹具”部分是完全相同的。

一切看起来都很完美，是不是？小编也希望世界是这么简单美好的。但残酷的现实摆在了面前，在很多情况下，去嵌以后的结果在频域上看起来很正常，但转到时域上，就出现了一些奇奇怪怪的东西。

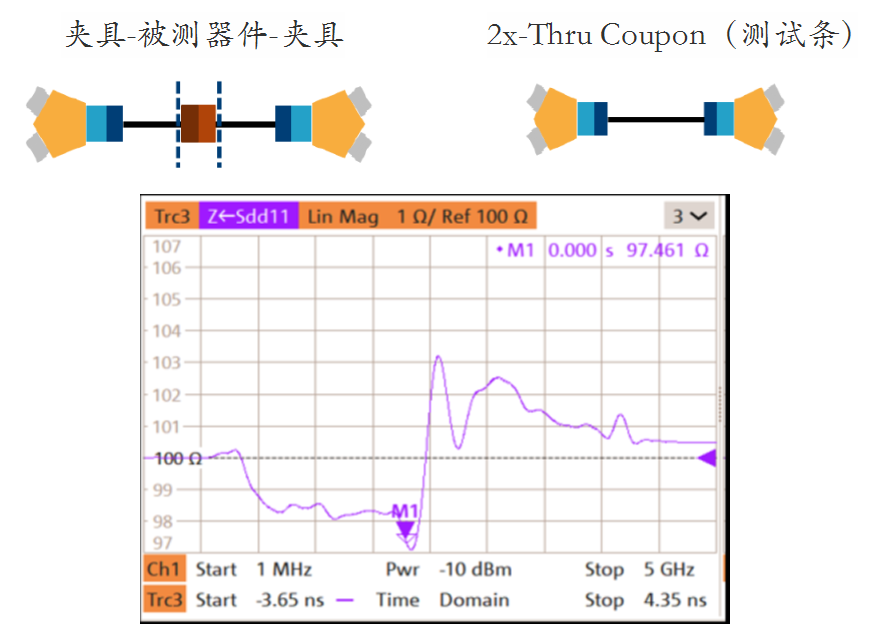
图7 去嵌结果中出现了奇奇怪怪的东西

这是一个差分连接器对的去嵌结构和去嵌以后的时域阻抗结果（这个例子是差分的，对于单端也是一样的）。图中“M1”的位置对应“0s”，而结果显示，在0s以前，阻抗就明显偏离的系统阻抗100Ω。这个结果被称为“非因果性”。因果性（Causality）这个词听起来有点哲学或佛学的味道，实际上也没那么复杂。我们的世界是一个因果的世界，有因才有果。那在咱们的电子电路领域，因果性意味着有激励才会有响应，响应不应早于激励。根据矢网时域测试原理，激励信号是在0s时刻产生的。在0s之前出现了偏离了系统阻抗的结果，是违背了因果性。这样的结果在现实世界中是不应该存在的。我们现在得到了这样一个结果，真相只有一个：一定是我们在哪一步中出现了问题。

经过各位前辈大佬们的努力工作，终于发现，引起这一问题的主要原因是我们做的第三个假设。在PCB场景中，由于公差控制、玻纤效应、连接器装配等等因素，“2x-Thru Coupon”中的左右侧夹具与“夹具-被测器件-夹具”中的左右侧夹具并不完全一致，尤其是他们的时域阻抗特性。对于线缆场景，情况也基本一致。我们来一起看一下上面的例子。

我们分别看一下“2x-Thru Coupon”和“夹具-被测器件-夹具”的时域阻抗：

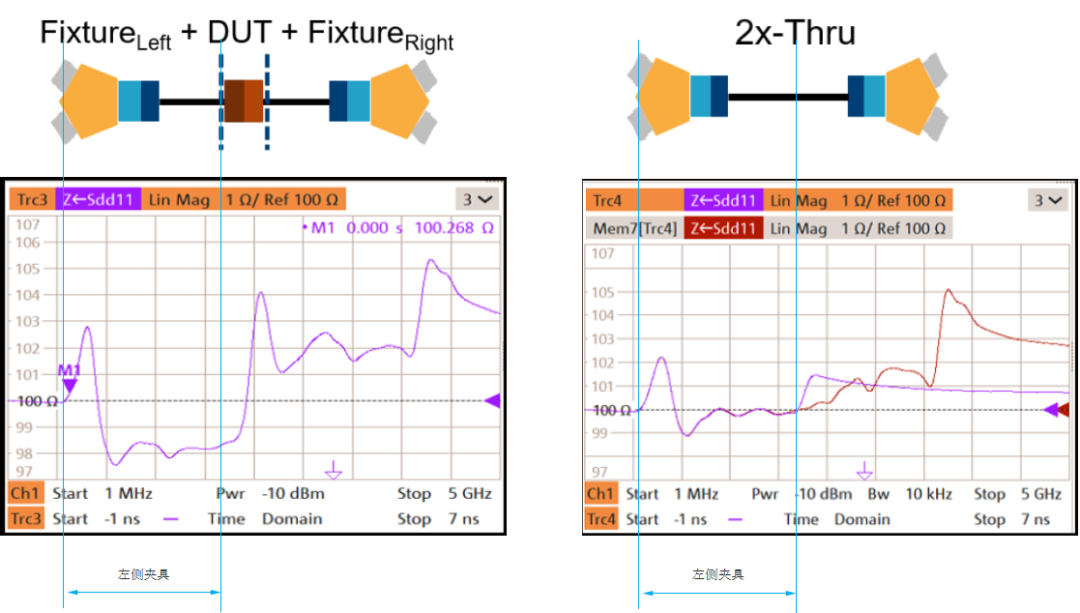
图8 时域阻抗对比

左图是“夹具-被测器件-夹具”的时域阻抗结果；右图中的紫色迹线为“2x-Thru Coupon”的时域阻抗结果，红色迹线为使用时域门以后得到的左侧夹具时域阻抗结果。可以看出，两个结果中，“左侧夹具”对应的时间范围内，虽然迹线的形状有点像，但还是有差别的，虽然差别只有1-2欧姆，但也足以造成我们去嵌结果的非因果性。

问题找到了，接下来的问题是如何解决这个问题。聪明的小伙伴可能已经想到了一个办法：前面的操作都一样，通过“2x-Thru Coupon”找到中点对应的时间，然后在“夹具-被测器件-夹具”的时域结果上下刀（Gating），得到

的时域结果，问题不就解决了吗？

这确实是一个解决问题的思路。但我们知道，所有的S参数都是相互关联的，也就是说

和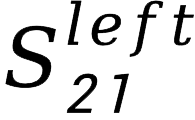、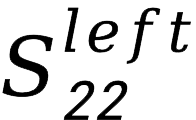互相影响的。用“夹具-被测器件-夹具”来获得

，用“2x-Thru Coupon”来获得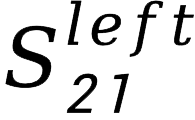、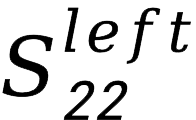，忽略了这些参数间的相互影响，会引起其他的问题的。

前辈大佬们采用了另外一种方法。把“左侧夹具”离散成一系列不同阻抗的均匀传输线级联。具体分成多少段，是由时域点数和“左侧夹具”的电长度决定的。对于每一段均匀传输线，需要两个参数来描述：特征阻抗

和传输常数

。

可以按上面的思路，由“夹具-被测器件-夹具”的时域结果逐段得到。

当然这里还隐含了一个假设：

为了得到传输常数

，

我们需要引入另一个假设：

假设Ⅳ：“2x-Thru Coupon”与“夹具-被测器件-夹具”的传输常数是均匀且一致的

基于这一假设，我们可以根据“2x-Thru Coupon”的测量结果得到每一段传输线的传输常数。这样我们即可以得到阻抗特性与“夹具-被测器件-夹具”完全一致的

，又兼顾了

和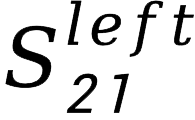、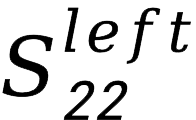之间的互相影响。这种方法就是我们说的“阻抗修正”去嵌入。

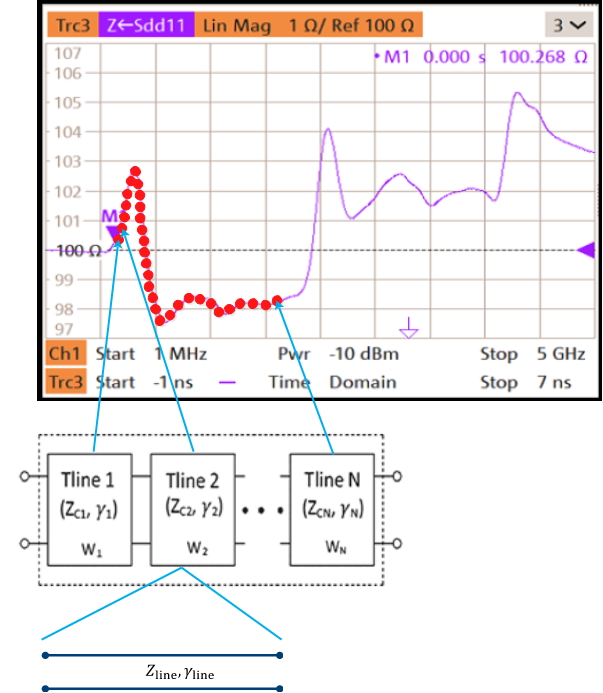
图9前辈大佬提出的解决方法

可以看出来，在“阻抗修正”去嵌入中，我们用假设IV代替了原来的假设III。

图 10是刚才的例子，采用了“阻抗修正”去嵌入技术得到的去嵌结果，与图 7对比，被测器件的时域阻抗特性更加合理，更加符合“因果性”。

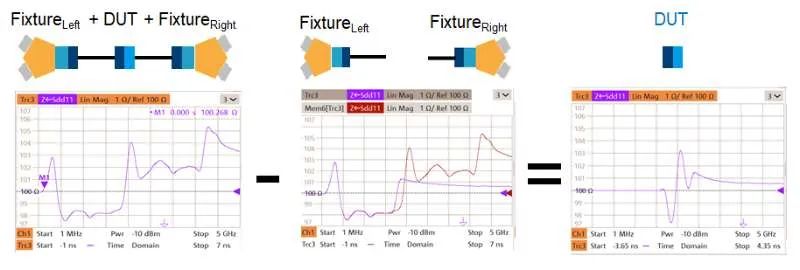
图10“阻抗修正”去嵌入结果

当然，假设IV也不是完美的，前辈大佬们认为由于引入了这一假设，“阻抗修正”去嵌入的

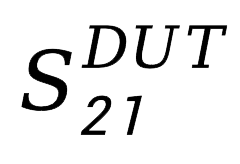
的结果比不做阻抗修正的去嵌入结果精度差。我们在工作对这一点没有明显的感觉，如果各位小伙伴遇到了有明显的差异，欢迎沟通交流。真要是遇到了，只能两害相权取其轻了，毕竟现在还没有一种面面俱到的完美方法。

另外我们还想提醒各位小伙伴一点：“阻抗修正”去嵌入也不是在所有的场景中都适用。比如被测器件是个带通滤波器，那么此时“夹具-被测器件-夹具”结构是无法得到时域阶跃响应结果的，因此不能适用“阻抗修正”去嵌入方法的。小伙伴们只需要在图 1中去掉“Impedance Correction（阻抗修正）”选项前面的“√”，就可以使用标准的去嵌入了。

审核编辑：黄飞