使用MD和MO/DFT计算相对介电常数

不同分子的相对介电常数计算

目的和方法

介电常数有三个分量：电子极化、离子极化和定向极化。在实验中，它们的总和被认为是介电常数，但在模拟中进行计算时，应选择合适的方法并对每种方法分别进行计算。

分子动力学计算(MD)

MD让我们可以估测分子因振动和取向产生的极化。相对介电常数可以由各个原子电荷偶极矩之和的时间波动得到，公式如下：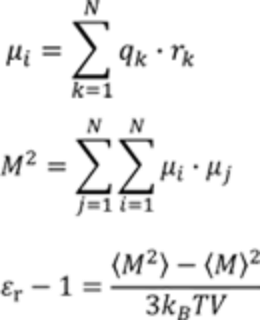
µi : 分子i的偶极矩

qk : 原子电荷

rk : 原子空间

M : 分子偶极矩之和

ε r : 相对介电常数

T: 系统温度

V: 系统体积
分子轨道法计算（MO）/密度泛函理论（DFT）计算

MO/DFT让我们可以估测电子极化，由分子极化率计算相对介电常数。

εr : 相对介电常数

ε0 : 真空介电常数

N : 电偶极子的数密度

α : 极化率

模拟成果

图2和表1给出了用MO和MD计算苯和丙酮的相对介电常数结果。其中MO估测值由高斯09测定的分子极化率和实验密度得出，MD估测值由300k和1百帕OPLS力场条件下计算液态体模型得出。在相同的OPLS力场中，丙酮的εMD也显示为15 [2]。因此J-OCTA的计算是有效的。

由于苯具有极高的对称性，几乎没有永久偶极子，使用MD来估测相对介电常数时因分子振动和取向引起的极化是非常小的。这表明大部分实验结果是由电子极化得出。而丙酮则相反，仅仅估测电子极化远远不够，同时估测取向极化也非常重要。

图1 仿真模型（左：苯环 右：丙酮）

图2 相对介电常数估测值
表1 相对介电常数估测值和偶极矩

相对介电常数 偶极矩
同时MD和QSPR（定量构效关系）也用来计算PVC聚合物的相对介电常数，其结果如表2和3所示。使用MD计算时，我们重复建10次建模过程并设置一个OPLS力场。我们把100个分子放入体系中，在300k和1百帕条件下释放，并在2毫秒体系达到平衡时根据MD计算出相对介电常数。MD计算出平衡时密度为1.32 g/cm3，相对介电常数为2.92。

用QSPR计算相对介电常数时显示密度为1.38g/cm3，相对介电常数为2.93，与MD结果相近。

图3 PVC仿真模型
（白色：氢 灰色：碳 绿色：氯）
表2 MD计算的相对介电常数与QSPR计算的相对介电常数

· 参考文献

· [1] J.Bicerano，《聚合物性能预测》，第三版，Marcel Dekker, 2002年

· [2] J. Chem.Eng. Data 2018, 63, 5, 1170

· [3]转载自上海庭田信息科技有限公司

审核编辑 黄宇