信号处理(Signal Processing)是对各种类型的电信号按各种预期的目的及要求进行加工过程的统称。它涵盖了模拟信号处理和数字信号处理两大领域。模拟信号处理主要关注对连续变化的模拟信号的处理,而数字信号处理则是对离散的数字信号进行处理。
信号处理的主要目的是提取信号中的有用信息。在这个过程中,信号可能会经历放大、滤波、去抖动、采样和重建等多种处理方法。例如,滤波可以通过特定的滤波器去除信号中的噪声或干扰,使原始信号更加清晰和准确。放大则通过放大电路增加信号的幅度,以提高信号的分辨率和检测灵敏度。去抖动方法如时钟同步、滑动平均和滞后滤波等,用于恢复信号的稳定性和准确性。采样和重建是数字信号处理中的关键步骤,用于将连续信号离散化为离散信号,同时保持信号的完整性和准确性。
信号处理常用算法简介
(1)变分模态分解(Variational Mode Decomposition,缩写VMD):模态分解认为信号是由不同“模态”的子信号叠加而成的,而变分模态分解则认为信号是由不同频率占优的子信号叠加而成的,其目的是要把信号分解成不同频率的子信号。
该算法,是目前超好用、普遍常用的算法。
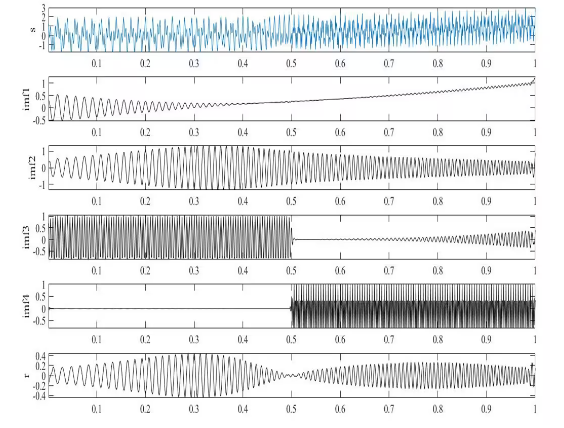
变频变幅信号作变分模态分解,得到4个固有模态函数imf1~4及余项r
(2)经验模态分解(Empirical Mode Decomposition,缩写EMD):是由黄锷(N. E. Huang)与其他人于1998年创造性地建立的一种自适应信号时频处理方法,特别适用于非线性非平稳信号的分析处理。
该算法,是目前好用、常用的算法,仅次于变分模态分解算法。

有周期成分和间歇成分的分段信号作经验模态分解,得到4个固有模态函数imf1~4及余项r
(3)小波分析(Wavelet):也叫“小波变换”,它通过伸缩和平移两种处理对信号(函数)逐步进行多尺度细化,最终达到在信号高频处实现按时间细分,在信号低频处实现按频率细分,能自动适应时频信号分析的要求,从而可聚焦到信号的任意细节,解决了Fourier变换的困难问题,成为继Fourier变换以来在科学方法上的重大突破。有人把小波变换称为“数学显微镜”。
该算法,比较陈旧,被前人用得较多。但仍然是目前好用、常用的算法,仅次于变分模态分解算法、经验模态分解算法。
(4)傅里叶变换(Fourier transform,缩写FT):有多个中文译名,常见的有“傅里叶变换”、“付立叶变换”、“傅立叶转换”、“傅氏转换”、“傅氏变换”、等等。
傅立叶变换是一种分析信号的方法,它可以分析信号的成分,也可用这些成分合成信号。许多波形可作为信号的成分,比如正弦波、方波、锯齿波等,傅立叶变换用正弦波作为信号的成分。
该算法,不陈旧、特经典,被前人和现人用得最多。仍然是目前超好用、普遍常用、必不可少的算法。
信号处理在多个领域都有广泛的应用。在移动通信中,数字信号处理技术能够实现信号的调制、解调和滤波,确保信号的稳定传输。在图像处理领域,数字信号处理技术可以用于图像增强、压缩和识别等。在声音处理领域,数字信号处理技术可以实现对音频信号的压缩编码,提高音频的传输效率和存储空间。此外,在雷达和声呐、医学成像等领域,数字信号处理技术也发挥着重要作用。
随着科技的进步,一些新的技术和产品也开始应用于信号处理领域。例如,RD芯片作为一款可重构的数字信号处理器,能够根据不同需求进行自我调整,实现处理效率和质量的双重提升。它在5G技术、图像处理、音频处理等领域展现出强大的实力,为用户带来更加细腻、清晰的视听体验。
审核编辑:黄飞
-
算法
+关注
关注
23文章
4620浏览量
93051 -
数字信号处理
+关注
关注
15文章
562浏览量
45902 -
信号处理
+关注
关注
48文章
1032浏览量
103315 -
函数
+关注
关注
3文章
4338浏览量
62740 -
傅立叶变换
+关注
关注
3文章
105浏览量
32415
发布评论请先 登录
相关推荐




 信号处理常用算法简介
信号处理常用算法简介











评论