陷波滤波器的相关知识

1. 引言

有鉴于数字信号处理涉及的面太多，我们必须要把话题收缩。数字滤波的种类也是五花八门，因此再选一个小的类型，我们将围绕离散线性时不变系统（Discrete Linear Time-Invariant System）来简单讨论一下陷波滤波器(Notch Filter)和梳状滤波器(Comb Filter)，通过代码的演示和输出，我们可以比较一下这两类滤波器的特点。在本文中我们先以陷波滤波器为题来讨论相关的内容。

关于滤波，我们多少会了解一些，诸如带通，带阻，高通，低通等特性。信号滤波，其实我们在很多的应用中都会不自觉地应用起来，比如ADC值的多次采样平均——这是一种典型的数字滤波方式，当然也是最简单滤波方式中的一种。

2. 关于线性移不变系统和数字滤波器

何谓线性移不变系统？主要是两点：

系统的弛豫状态满足可叠加原理（表现为线性，比例性）

系统的弛豫状态时移不变,即任意时间平移量k，有x(n-k)→T→ y(n-k) )

再加上系统是因果的（如果一个系统的输出仅仅依赖于过去和现在的输入，而不依赖于未来的输入，那么此系统就被称为因果系统），稳定的（系统输出不是发散振荡的），就构成我们滤波器的几个基本要素。

一个弛豫的系统是指当初始时刻系统内部无能量或所有状态变量的初值为零的系统，也就是说该系统的所有状态变量都已经"弛豫"到它们的稳定或静态值。在弛豫条件下，系统中不存在任何内部能量或动力以推动系统产生输出。换句话说，所有的输出都将仅被输入驱动。

在差分方程或差分方程系统中，所谓的"初始条件为零"或"弛豫的初始条件"，意味着所有的y(n)（对于n<0）都被假定为零，即系统在开始接收输入（即n=0）之前是"静止"或"弛豫"的。对于许多系统和信号处理分析，完全弛豫的假设能够简化计算和分析过程。然而，实际上，实际的物理系统可能需要一些时间才能达到完全弛豫的状态。

离散数字滤波器在时域上可以用常系数差分方程来表示：

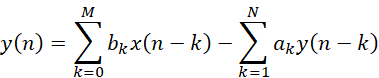
（1）

其中ak，bk都是已知常数，但是该方程中，并不能直接看到y(n)和x(n)之间的等式关系，实际应用最好通过软件迭代的方式才方便处理。我们以参考书本[1]上的例子简单说明。假如一个递归的输入输出方程有：

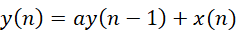
设定对n<0的输入信号不计，输出部分只考虑y(-1),那么省掉递推过程，可以得到：

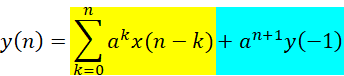
，其中n>0

y(n)的结果表达式中，第一部分是系统的零输入响应，第二部分是零状态响应（颜色区分）。如果该系统的初始状态是弛豫的，即有：

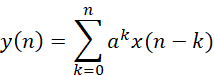
关于系统的线性，从上式可以知道，对于系统S和任意输入x1,x2和常数c1,c2，有如下等式说明当前系统是满足叠加性的，因此系统是线性的。

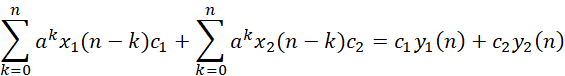
其中关于两个响应的说明：

零状态响应（ZSR）：这是指当系统的初始状态为零，即没有存储的能量和信息，对系统的新输入信号产生的响应。这个响应完全由当前的输入驱动，和系统在初始时刻的状态无关。ZSR是系统特性（如系统函数、冲激响应等）和输入信号的函数。

零输入响应（ZIR）：这是指当系统的输入为零，即没有新输入信号，系统由其初始状态或初始条件产生的响应。这通常描述了系统如何在没有外部输入的情况下，自然地演化和衰减，即系统的自由响应。ZIR仅仅取决于系统的特性和初始状态

上面的结论是通过简单的时域例子来说明的，可能无法代表全状态的方程。我们通过对式-1单边Z变换的方式从复频域的角度来加深理解一下(将Z=e^jω带入，就转入频域)。单边Z变换中，输入信号x(n)被认为是因果的，因此不考虑x(n),n<0的输入，并且以前的输入所有信号的作用都反映在初始条件y(-1),y(-2)，…,y(-N)上。将式-1经过单边Z变换，我们可以得到[1]：

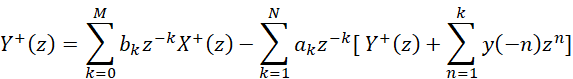
(2)

式-2经过合并可得（式-3）：

(3)

式-3中，前半部分就是系统的零状态响应；后半部分就是零输入响应，和系统以前的状态相关。系统的响应组成和在时域的响应组成是相同的。而且我们也知道，复频域中，下面的系统等式也是属于LTI的：

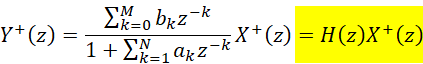
(4)

对于一般性的我们有：

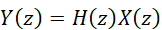
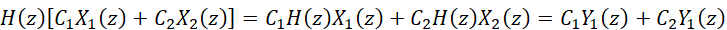    (5)

式-5所表达的系统在复频域的弛豫状态，是满足叠加性要求的，因此系统是线性的。

我们再看关于系统符合线性系统的其他要求：

总响应等于零输入响应和零状态响应之和；

零状态响应满足叠加法则；

零输入响应满足叠加法则。

关于系统时移，我们知道，在时域的时移，对应复频域中在z平面上的旋转：

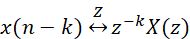
如果将z=e^jω代入，就可以将式-4转换到频域的输入到输出的频幅响应。我们有：

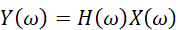
此时如果输入信号有时移x(n-k)，我们得到的系统响应将是：

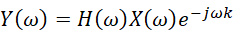
这种情况下，无论e^(-jωk)是系统的频率响应H(ω)引起的相应变化，还是输入信号X(ω)本身的时延引起的相位变化，效果是一样的。另外，如果频率响应H(ω)对输入信号的幅度有同样的缩放功能|H(ω)|。这些对于信号本身可以不认为是失真的。

事实上，线性时不变系统和滤波器这两个术语是同义的。某种意义上，H(ω)对于输入信号中不同的频率成分起着加权函数或频谱整形函数的作用[1]。这就是我们围绕系统函数H(ω)展开如何设计滤波器的由来。

既然这里又回到了滤波器这个话题，我们再将内容收缩一下，从陷波滤波器开始。式-1中，如果任意a_k=0，那么这个系统属于有限冲激响应系统(FIR)；有任意a_k≠0，就会被称之为无限冲击响应系统（IIR）。

3. 陷波滤波器(Notch Filter)

陷波滤波器，也称为陷带滤波器，是一种在某一特定频率或者频率范围上，将信号的幅度衰减到极低甚至为零的滤波器。它属于带阻滤波器的特例，带阻滤波器是一种抑制某一频带内的信号而允许频带以外的信号通过的滤波器。它们的区别在于陷波滤波器的阻止带宽通常更窄，目标更准确。如果是针对某个单一频率的信号进行滤波，那么该滤波器的品质因数Q值的要求也会更高，以便让被阻止的带宽足够窄而不影响该频率附件信号的传递。但是过高的Q值就可能会引起滤波器的抖动，这个我们在设计滤波器的过程中，是需要留意的。

陷波滤波器的特性：

目标频率或频道的信号被显著削弱，而其他频率的信号几乎不受影响。

陷波频率或频带的选择往往能够调整。

能有效削弱或消除特定频率的噪声或干扰。

应用场合：

音频处理：在音乐制作或音频修复中，陷波滤波器用于消除特定的干扰音，例如电流电压的噪声。

工业现场信号采集处理系统：比如用于滤除50或60Hz的工频噪声。

通信系统：超窄带陷波滤波器用于从广带信号中选择性地滤除某一特定信号。

医疗和生物工程：用于消除生物和医疗信号中的电源频率以及任何周期性干扰。

雷达和导航系统：从信号中移除某一特定频率的干扰。

陷波滤波器为了更准确抑制特定频段的信号而设计，因此相比普通带阻滤波器，它的阻带通常会设置得更窄更精确。

我们通过模拟信号以及滤波处理后的信号之间进行对比，来了解这种类型滤波器的特点。

模拟信号中有50Hz的工频干扰信号需要滤除，保留20Hz的有用信号。先看结果，后查代码[2]（在本文的最后部分）。

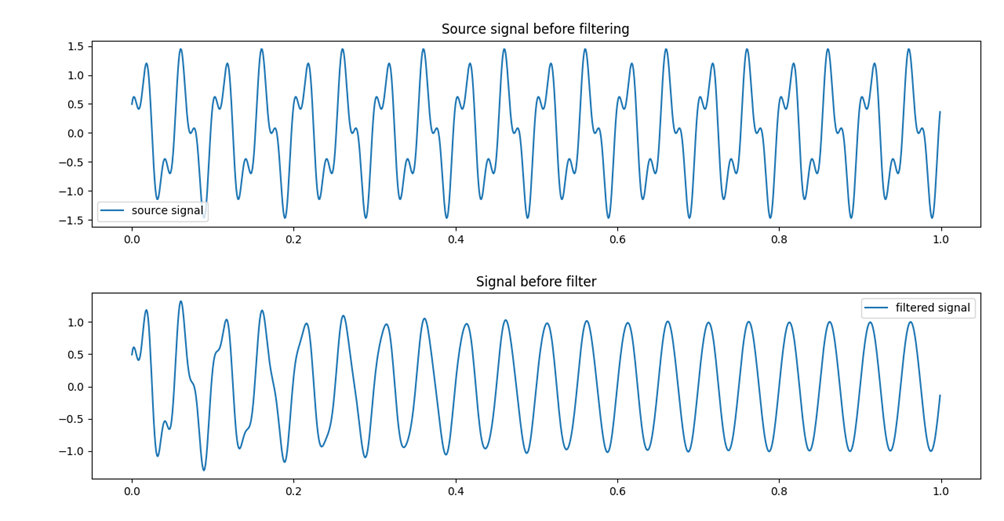
图-1 信号滤波前后对比

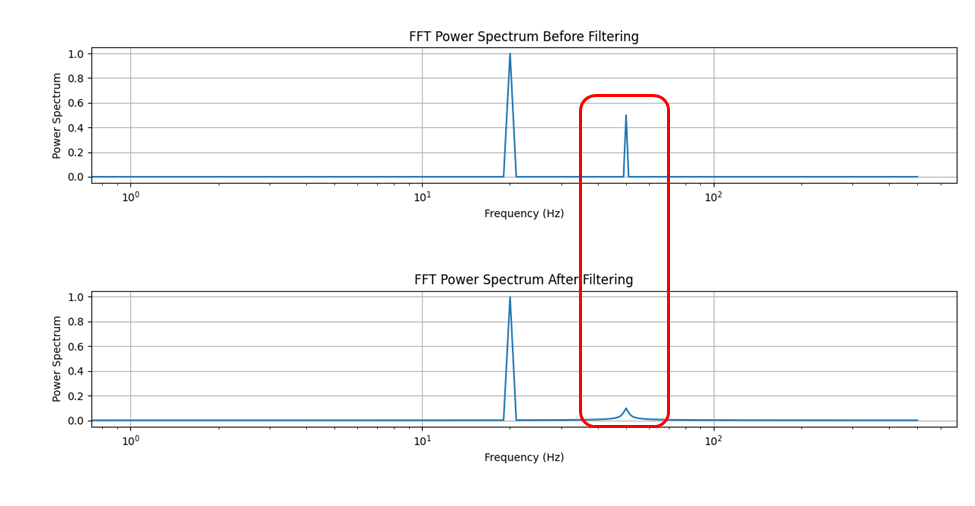
图-2 信号滤波前后的频谱图（削弱后的50Hz信号）

第三个图，是我们陷波滤波器典型的特征图。在指定的频率处对输入信号进行衰减，而其他频率处保持通过。

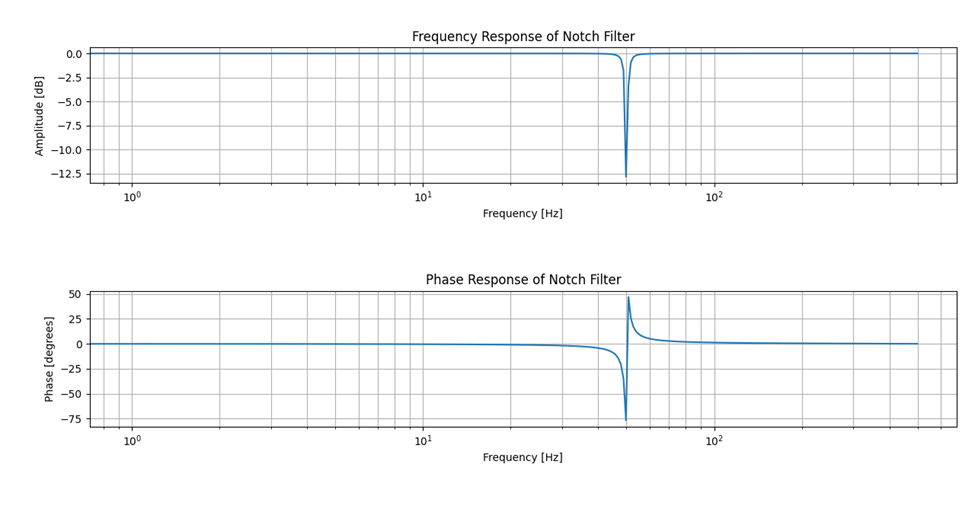
图-3 滤波器的幅相频响应图

该2阶IIR滤波器在50Hz之外的频域的信号都可以保持的通过性。参数如下（程序中有输出）：

b0~b2: [ 0.99479124, -1.89220538, 0.99479124]

a0~a2: [ 1.0 , -1.89220538, 0.98958248]

对应的系统函数有：

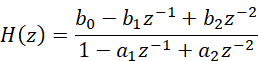
(6)

陷波滤波器对于特定的频率过滤有其独到的用途。该模拟测试程序可以在本文的附页部分查看。通过计算得到系统函数在z平面中对应的零点和极点结果如下(本文最后提供计算代码)：

	零点1	零点2=零点1*
结果	0.9510565151337682+0.3090169979493239j	0.9510565151337682-0.3090169979493239j
绝对值	1.0	1.0
相角	18.00000021533598°	-18.00000021533598°
	极点1	极点2=极点1*
结果	0.94610269+0.3073632703736149j	0.94610269-0.3073632703736149j
绝对值	0.9947776032862823	0.9947776032862823
相角	17.997582759707843°	-17.997582759707843°

在设计二阶Notch滤波器时，零点和极点的位置和数值对滤波器的性能起着关键的作用。在上面的模拟的滤波器中，z平面中的2个零点就在单位圆上，不过两个极点已经很靠近单位圆了，实际应用中需要进一步测试验证以避免滤波器的额外抖动。

大家可以尝试用C/C++的方式将参数转换为代码，成为你所需的滤波器。这里使用的是Python中的IIR方式，而如果真要用FIR方式实现同样的效果，通常会需要很高的滤波器阶次，反而会导致计算复杂度增加，响应也会滞后。以下是设计陷波滤波器的一些基本的要求：

零点的位置：Notch滤波器的零点通常被放在单位圆上，其位置决定了阻止频率的相关位置。要阻止的频率就是零点所在的角度对应的频率。

极点的位置：极点的位置靠近零点可以产生较窄的Notch带宽，这意味着滤波器能够拒绝的频率范围较窄。相反，如果极点离零点较远，那么Notch带宽将较宽。但需要注意的是，极点的位置必须在单位圆内，否则滤波器将不稳定。

零点和极点的数值：这些数值决定了滤波器的具体阻止频率和带宽。通过精确地选择这些数值，可以设计出满足各种应用要求的滤波器。

总的来说，设计Notch滤波器时，需要根据具体的阻止频率和带宽需求，精确地调整零点和极点的位置和数值。并且要确保极点的位置在单位圆内，以保证滤波器的稳定。具体数值的确定可以借助各种滤波器设计工具进行计算。

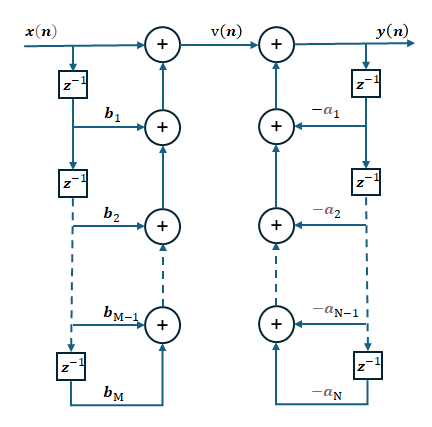
图-4 滤波器的信号传递

4. 小结

在本文中，我们详细探讨了Notch滤波器的设计和应用。我们理解了Notch滤波器的工作原理以及如何有效消除特定频率的干扰。此外，我们还简单了解了如何根据需求对滤波器进行设计，特别是零点和极点的定位。

通过理解和正确应用这些原则，我们可以设计出性能优秀的Notch滤波器，这对于许多应用场景，如信号处理，噪声消除等领域都是非常重要的。在很多工业现场的传感器应用中，会涉及很多信号的相对高速采集的场合，会用到Notch滤波器，尤其针对诸如工频干扰，或者特定频率的过滤等。

安费诺传感器（Amphenol Sensors）提供诸多满足您应用的可靠、准确高精度的传感器，但如果实际应用过程中碰到一些异常的信号，可以和我们一起来分析原因，解决问题，根据实际工况来改善应用。

后续的文档中，我们将简单讨论另一种滤波器——梳状滤波器（Comb Filter），并通过Python模拟该滤波器的功能和实现，以及一些特情的处理方式。

陷波滤波器模拟测试Python代码

import numpy as np
import matplotlib.pyplot as plt
from scipy import signal
from scipy import fft,fftpack


# 采样频率
fs = 1000
# 设计带阻滤波器，过滤50Hz噪声
f0 = 50.0 # Frequency to be removed from signal (Hz)
Q = 30.0 # Quality factor
w0 = f0/(fs/2) # 设计归一化频率
b, a = signal.iirnotch(w0, Q)


# 生成一段带噪音的信号
t = np.arange(0, 1.0, 1/fs) # Time vector
x = np.sin(2*np.pi*20*t) # 20Hz sine wave
x = x + 0.5*np.cos(2*np.pi*f0*t + .1) # 50Hz sine wave


# 设计滤波器并应用
yi = signal.lfilter(b, a, x)
# 输出该滤波器的参数
print("Filter Parameters:","b:",b,"a:",a)
# 绘制信号的波形图
plt.figure(1)
plt.subplot(211)
plt.title('Source signal before filtering')
plt.plot(t, x, label='source signal')
plt.legend()
# 绘制信号的频谱图
plt.subplot(212)
plt.title('Signal before filter')
plt.plot(t, yi, label='filtered signal')
plt.legend()
plt.tight_layout()
plt.show()


# 进行FFT变换
xf = np.linspace(0.0, 1.0/(2.0/fs), fs//2)
signal_original = fftpack.fft(x)    # 源信号的FFT
signal_filtered = fftpack.fft(yi)   # 滤波之后的FFT


# 绘制信号的FFT图
plt.figure(figsize=(8, 4))


plt.subplot(2, 1, 1)
plt.semilogx(xf, 2.0/len(x) * np.abs(signal_original[0:len(x)//2]), label='source signal')
plt.title('FFT Power Spectrum Before Filtering')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power Spectrum')
plt.grid()


plt.subplot(2, 1, 2)
plt.semilogx(xf, 
             2.0/len(signal_filtered) * np.abs(signal_filtered[0:len(signal_filtered)//2]), 
             label='filtered signal')
plt.title('FFT Power Spectrum After Filtering')
plt.xlabel('Frequency (Hz)')
plt.ylabel('Power Spectrum')
plt.grid()
plt.tight_layout()
plt.show()


# 绘滤波器的幅度频响应和相频响应
freq, h = signal.freqz(b, a, fs=fs)


plt.figure(figsize=(8, 4))
plt.subplot(2, 1, 1)
plt.semilogx(freq, 20*np.log10(abs(h)))
plt.title('Frequency Response of Notch Filter')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Amplitude [dB]')
plt.grid(which='both', axis='both')


angle = np.unwrap(np.angle(h))
plt.subplot(2, 1, 2)
plt.semilogx(freq, angle * 180 / np.pi)
plt.title('Phase Response of Notch Filter')
plt.xlabel('Frequency [Hz]')
plt.ylabel('Phase [degrees]')
plt.grid(which='both', axis='both')
plt.tight_layout()
plt.show()

通过滤波器的参数计算滤波器Z平面的零、极点(Zero/Pole)的Python

import cmath
import math
# 定义系数
b = [0.99479124, -1.89220538, 0.99479124]   # 用新的参数替换掉表中的
a = [1.0, -1.89220538, 0.98958248]


# 计算0点
zero1 = (- b[1] + cmath.sqrt(b[1]**2 - 4 * b[0] * b[2])) / (2 * b[0])
zero2 = (- b[1] - cmath.sqrt(b[1]**2 - 4 * b[0] * b[2])) / (2 * b[0])


# 计算极点
pole1 = (- a[1] + cmath.sqrt(a[1]**2 - 4 * a[0] * a[2])) / (2 * a[0])
pole2 = (- a[1] - cmath.sqrt(a[1]**2 - 4 * a[0] * a[2])) / (2 * a[0])


# 计算相位角
zero1_abs = abs(zero1)
zero2_abs = abs(zero2)
pole1_abs = abs(pole1)
pole2_abs = abs(pole2)


zero1_angle = cmath.phase(zero1)
zero2_angle = cmath.phase(zero2)
pole1_angle = cmath.phase(pole1)
pole2_angle = cmath.phase(pole2)


phase_degrees_zero1 = math.degrees(zero1_angle)
phase_degrees_zero2 = math.degrees(zero2_angle)
phase_degrees_pole1 = math.degrees(pole1_angle)
phase_degrees_pole2 = math.degrees(pole2_angle)


print("Zeros: ", zero1, zero2)
print("Poles: ", pole1, pole2)
print("Zeros Angles: ", zero1_angle, zero2_angle, "abs Zeros:", zero1_abs, zero2_abs)
print("Poles Angles: ", pole1_angle, pole2_angle, "abs Poles:", pole1_abs, pole2_abs)
print("零点相位的度数为：", phase_degrees_zero1,phase_degrees_zero2)
print("极点相位的度数为：", phase_degrees_pole1,phase_degrees_pole2)