在上一个文档里,我们提到了FIR系统在时域的分段卷积中使用“重叠保留(Overlap-Save)”的处理方式,这里我们续集,说明一下“重叠相加(Overlap-Add)”的处理方式。 信号处理在时域和频域中处理是有差异的。 说得通俗一点就是:时域中处理是直接用采集到的信号进行计算;而频域中则要用离散傅里叶变换(DFT)/离散傅里叶反变换(IDFT)对采集到的信号进行转换到频域,然后再从频域转回时域处理。
在我们看到的参考文档[1]中,描述的是在频域进行DFT,然后由IDFT转回时域处理的过程。如下图所示。大概的过程是:
每次处理的数据长度为L,然后在每分段的尾部添加(M-1)个0之后,让每次处理的数据序列长度N=L+M-1,通常N为2的幂次倍;
同时对于滤波器,也需要将原来长度为b的序列,通过填0的方式增加到长度为N;
由DFT将两个数列分别转换到频域,相乘后,再IDFT转回时域,就得到N=(L+M-1)的时域卷积结果;
保留每次操作的所有数据,然后在下一次操作结束后,将最新数据的最前面的(M-1)个结果数据和上一次结果数据的最后(M-1)个数据顺序相加......持续直至结束。
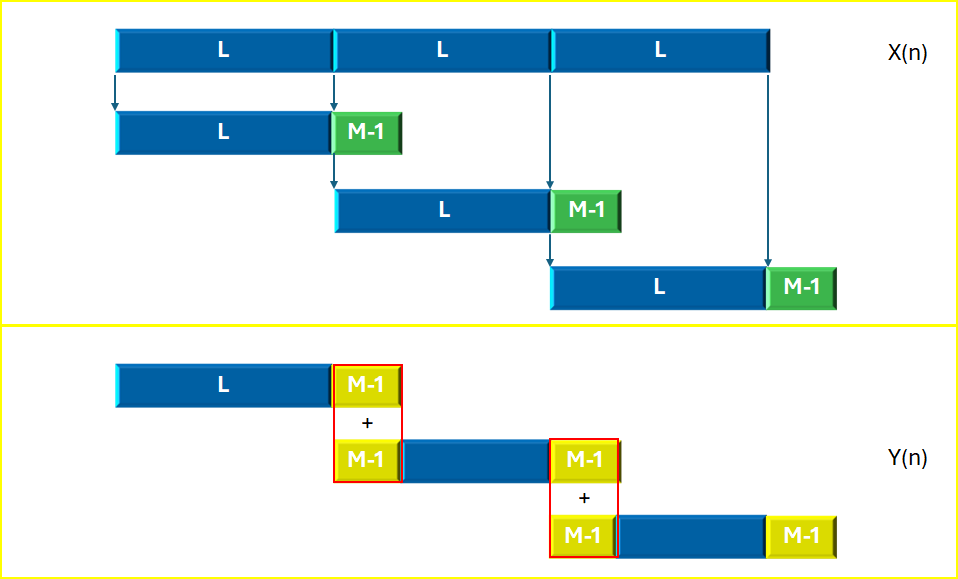
FIR频域的重叠相加示意图
我们看看时域的卷积应该怎么操作。
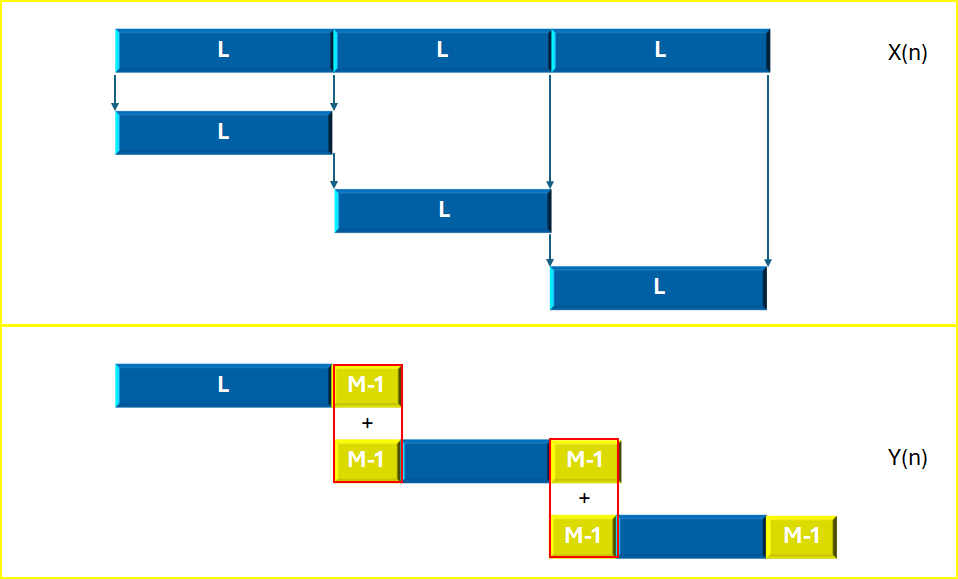
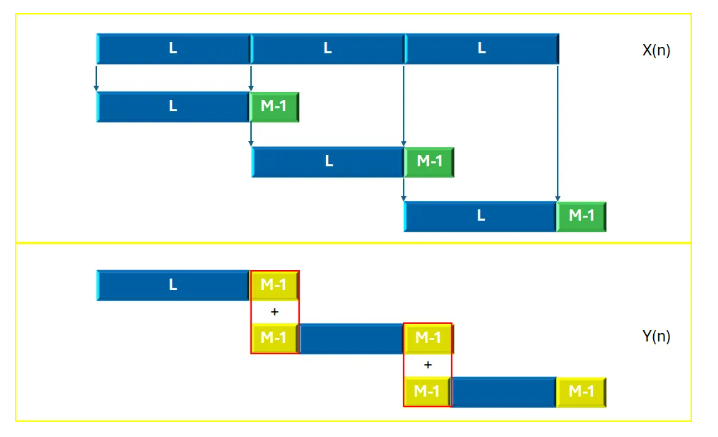
FIR时域重叠相加操作示意图
如上图所示:
每次读取长为L的数据序列,然后与长度为M的滤波器进行卷积,生成一个(L+M-1)的卷积结果序列;
保留每次操作的所有数据,然后在下一次操作结束后,将最新数据的最前面的(M-1)个结果数据和上一次结果数据的最后(M-1)个数据顺序相加......持续直至结束。
两个过程看起来略有差异,甚至会觉得时域的处理更简单省事,会不会更省时?其实频域看起来费时,但数据规模到了一定程度之后,频域的处理速度就具有优势了。然而对于一般的应用,直接卷积操作还是可以接受的。
还记得上次我们提到Python中卷积函数np.convolve的三种模式吧?该函数对卷积是在时域中进行的。
在Python中,卷积函数np.convolve(data_segment, b, mode)对指定长度的数据data_segment(长度L),和FIR滤波器系数序列b(长度M)进行卷积。输出的结果序列则分为以下三种:
full:结果长度=M+L-1
same:结果长度=max(M,L)
valid:结果长度=max(M,L)-min(M,L)+1=L-(M-1)
在这里,我们需要选用full模式,这样就获取每段卷积一个不落的所有数据(L+M-1)。先看模拟效果后看Python代码。 故事情节设定:50Hz的信号中,夹杂300,450Hz的干扰。滤除干扰。
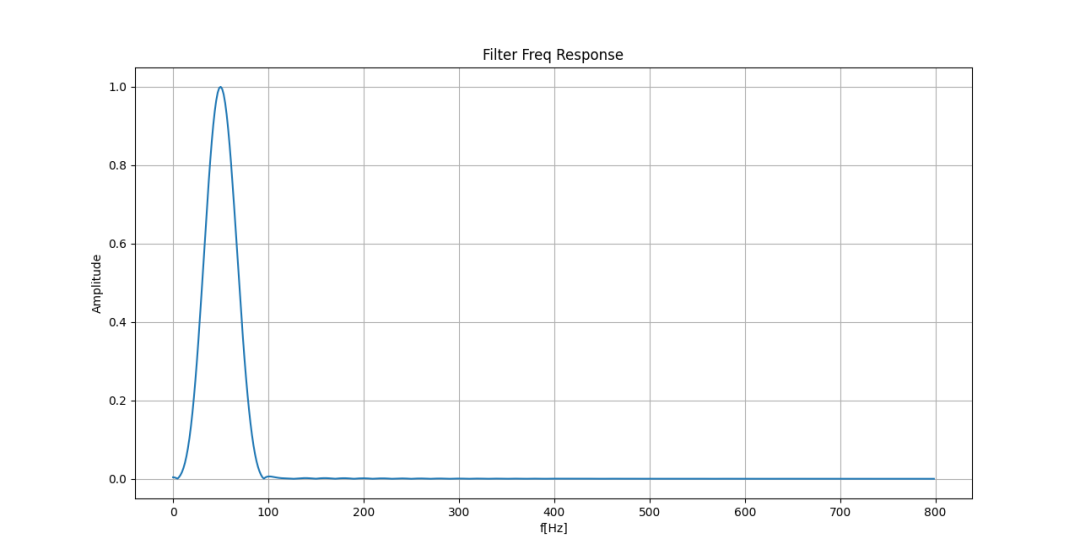
FIR选频滤波器的幅频响应
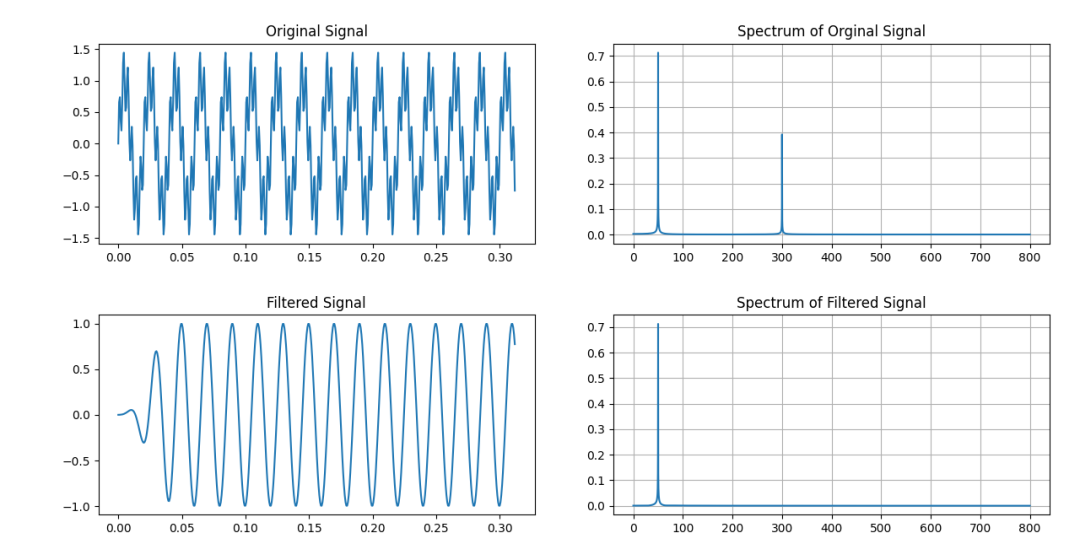
FIR系统重叠相加的滤波结果示意图
这里要特别说明一点:卷积后的数据长度,最终会比原来的数多出(M-1)个,所以输出到图的时候,需要有意控制长度。 滤波过程中要经历“热身”,所以最开始阶段有(M-1)个数据也是可以剔除的。同样,如果我们看卷积最终结果尾部不处理,也有(M-1)个无效数据的输出需要截取。
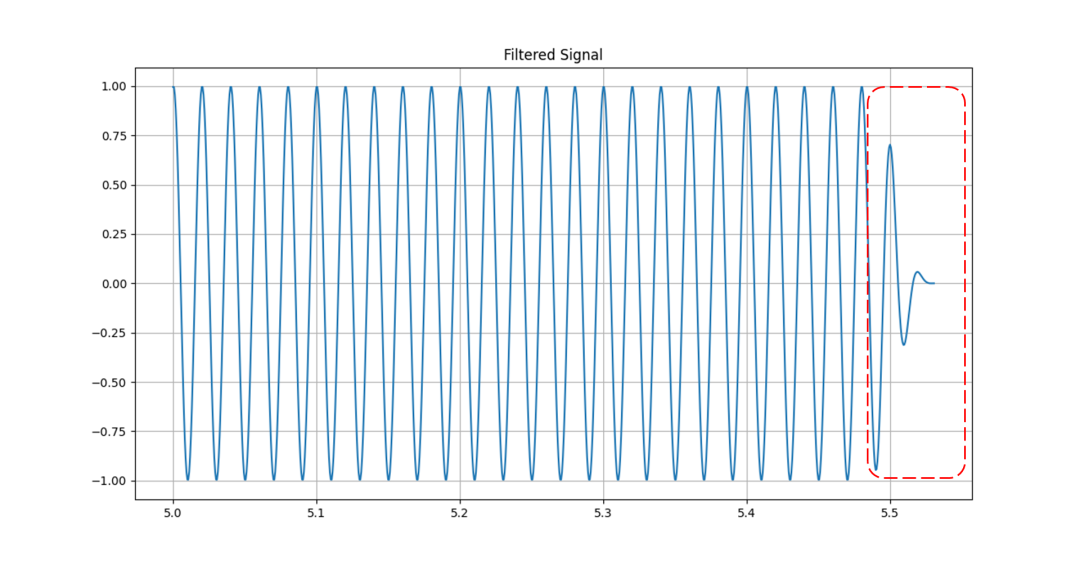
卷积后尾部无效数据(M-1)
上代码,我们自己在代码中划重点,并调整输出结果的有效长度范围:
import numpy as np import matplotlib.pyplot as plt from scipy import signal from scipy.fft import fft import math # 创建带通滤波器 f1 = 40 f2 = 60 filter_len = 80 # 滤波器长度 fs = 1600 # 采样频率维持不变 b = signal.firwin(filter_len, [f1, f2], pass_zero=False, fs=fs) # 设置数据长度 seg_filter_len = 256 # filter output length of each segment data segment_len = seg_filter_len - filter_len + 1 # 分段数据目标长度 seg_filter_len = segment_len + filter_len - 1 target_length = segment_len * 50 # 总数据长度 # 而新的时间序列的上限 b bspace = target_length / fs # 生成的时间序列为L的整数倍,模拟每次采样的数据的长度 t = np.arange(0, bspace, 1/fs) # 产生一个含有300Hz,450Hz和50Hz信号的模拟信号 x = np.sin(2 * np.pi * 50 * t) + 0.5 * np.sin(2 * np.pi * 300 * t) + 0.5 * np.sin(2 * np.pi * 450 * t) segments = [] for i in range(0, len(x), segment_len): segments.append(x[i:i+segment_len]) #Filtering&Overlap-Add processing # Total outputput buffer, len = target_length + filter_len - 1 filtered_signals = np.zeros(target_length + filter_len - 1) for i in range(len(segments)): filtered_segment = np.convolve(segments[i], b, mode='full') # full模式用于保留所有卷积结果 N = L + M -1 filtered_signals[i*segment_len:i*segment_len+len(filtered_segment)] += filtered_segment # 叠加过程 filtered_signals = filtered_signals#[:target_length] # 保留和原信号等长的部分 #FilterFreqResponse w, h = signal.freqz(b, 1, fs=fs) plt.figure() plt.plot(w, abs(h)) plt.title('Filter Freq Response') plt.grid() plt.xlabel('f[Hz]') plt.ylabel('Amplitude') # Signal Before filtering & Spectrum n = len(x) freq = np.fft.fftfreq(n, 1/fs) y = np.fft.fft(x) plt.figure() plt.subplot(221) plt.plot(t[:500], x[:500]) plt.title('Original Signal') plt.subplot(222) plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 标幺,绘制前一半 plt.title('SpectrumofOrginalSignal') plt.grid() #SignalAfterfiltering & Spectrum n = len(x) y = np.fft.fft(filtered_signals) plt.subplot(223) # 1. Normal output plt.plot(t[:500], filtered_signals[:500]) plt.title('Filtered Signal') plt.subplot(224) plt.plot(freq[:n//2], np.abs(y[:n//2]*2/n)) # 标幺,绘制前一半 plt.title('Spectrum of Filtered Signal') plt.grid() plt.tight_layout() plt.show() # 2. End of convolution without end cutoff: for test purpose plt.figure() temp = t[8000:8850] s = filtered_signals[8079:8929] plt.plot(temp, s) plt.title('Filtered Signal') plt.grid() plt.show()
-
数字滤波器
+关注
关注
4文章
270浏览量
47083 -
FIR
+关注
关注
4文章
147浏览量
33271 -
信号
+关注
关注
11文章
2804浏览量
77070
原文标题:数字滤波器(5)—FIR连续采样分段卷积时域重叠相加法
文章出处:【微信号:安费诺传感器学堂,微信公众号:安费诺传感器学堂】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
求函数计算序列线性卷积结果
毕业设计_分段卷积MATLAB仿真与DSP实现
串行结构的FIR滤波器设计(含文档 代码资料)
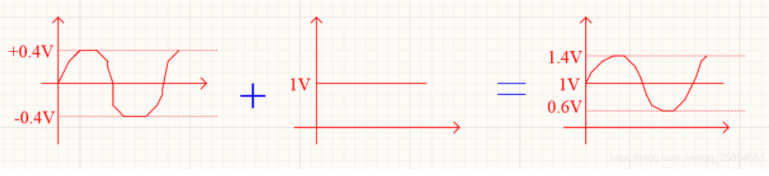
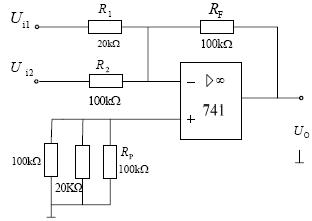
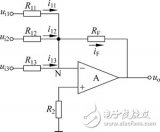
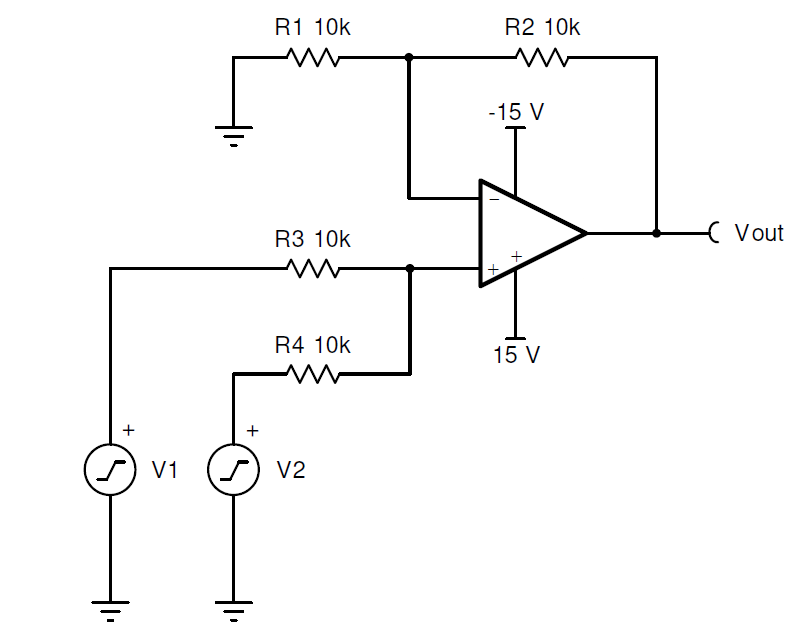
同相加法器电路原理与同相加法器计算
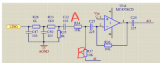
加法器与减法器_反相加法器与同相加法器
连续时间系统时域分析的MATLAB实现




 FIR连续采样分段卷积时域重叠相加法
FIR连续采样分段卷积时域重叠相加法











评论