神经网络是一种强大的机器学习模型,它通过模拟人脑神经元的连接方式来处理复杂的数据。神经网络的核心是前向传播和反向传播算法。本文将详细介绍神经网络的前向传播和反向传播的区别,并探讨它们在神经网络训练过程中的作用。
1. 前向传播(Forward Propagation)
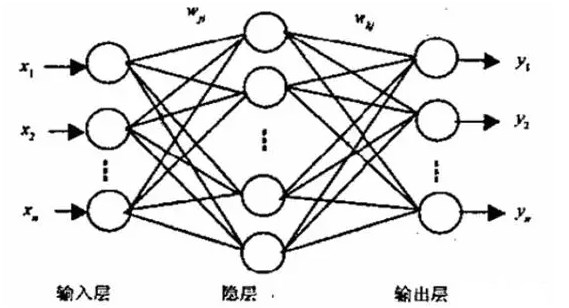
前向传播是神经网络在接收输入数据后,通过一系列计算得到输出结果的过程。这个过程是自下而上的,从输入层开始,逐层向上传递,直到输出层。
1.1 输入层
输入层是神经网络的第一层,它接收外部数据作为输入。输入数据可以是图像、文本、音频等多种形式。输入层的神经元数量取决于输入数据的特征维度。
1.2 隐藏层
隐藏层是神经网络中的中间层,它们对输入数据进行处理和转换。隐藏层的数量和每个隐藏层中的神经元数量可以根据问题的复杂性进行调整。每个隐藏层的神经元都会接收来自前一层的输出作为输入,并通过激活函数进行非线性变换。
1.3 激活函数
激活函数是隐藏层中的关键组成部分,它负责引入非线性,使得神经网络能够学习和模拟复杂的函数映射。常见的激活函数有Sigmoid、Tanh、ReLU等。
1.4 输出层
输出层是神经网络的最后一层,它负责生成最终的预测结果。输出层的神经元数量取决于任务的类型,例如分类任务的输出层神经元数量通常等于类别数。
1.5 前向传播的计算过程
前向传播的计算过程可以概括为以下几个步骤:
- 初始化输入数据。
- 将输入数据传递给输入层。
- 对输入层的输出进行加权求和,并加上偏置项。
- 将加权求和的结果通过激活函数进行非线性变换。
- 将激活函数的输出传递给下一层。
- 重复步骤3-5,直到达到输出层。
- 输出层的输出即为神经网络的预测结果。
2. 反向传播(Backpropagation)
反向传播是神经网络在训练过程中,根据预测结果与真实结果之间的误差,通过梯度下降算法调整网络参数的过程。这个过程是自上而下的,从输出层开始,逐层向下传递,直到输入层。
2.1 损失函数
损失函数是衡量神经网络预测结果与真实结果之间差异的函数。常见的损失函数有均方误差(MSE)、交叉熵(Cross-Entropy)等。
2.2 梯度计算
梯度是损失函数对网络参数的偏导数,它指示了损失函数在参数空间中增长最快的方向。通过计算梯度,我们可以知道如何调整参数以减小损失。
2.3 链式法则
反向传播的核心是链式法则,它允许我们从输出层开始,逐层向上计算每一层的梯度。链式法则的基本原理是将损失函数对输出层的梯度,通过激活函数的导数,逐层传递到输入层。
2.4 参数更新
在计算出每一层的梯度后,我们可以使用梯度下降算法或其他优化算法来更新网络的参数。参数更新的目的是减小损失函数的值,从而提高神经网络的预测性能。
2.5 反向传播的计算过程
反向传播的计算过程可以概括为以下几个步骤:
- 计算损失函数的值。
- 根据损失函数对输出层的梯度,使用链式法则计算隐藏层的梯度。
- 将梯度传递到每一层的权重和偏置项。
- 使用梯度下降算法或其他优化算法更新网络的参数。
- 重复步骤1-4,直到达到预定的迭代次数或损失函数的值达到满意的水平。
3. 前向传播与反向传播的区别
前向传播和反向传播是神经网络训练过程中的两个关键步骤,它们在功能和计算过程上有明显的区别:
- 功能 :前向传播负责生成预测结果,而反向传播负责根据预测结果与真实结果之间的误差调整网络参数。
- 计算方向 :前向传播是自下而上的计算过程,从输入层开始,逐层向上传递;反向传播是自上而下的计算过程,从输出层开始,逐层向下传递。
- 激活函数 :在前向传播中,激活函数用于引入非线性;在反向传播中,激活函数的导数用于计算梯度。
- 参数更新 :前向传播不涉及参数更新,而反向传播通过梯度下降算法或其他优化算法更新网络的参数。
-
神经网络
+关注
关注
42文章
4785浏览量
101276 -
模型
+关注
关注
1文章
3372浏览量
49314 -
神经元
+关注
关注
1文章
368浏览量
18526 -
机器学习
+关注
关注
66文章
8453浏览量
133165
发布评论请先 登录
相关推荐
解读多层神经网络反向传播原理
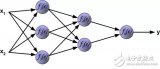




 神经网络前向传播和反向传播在神经网络训练过程中的作用
神经网络前向传播和反向传播在神经网络训练过程中的作用










评论