BP神经网络(Backpropagation Neural Network)是一种多层前馈神经网络,具有强大的非线性映射能力,广泛应用于模式识别、信号处理、预测等领域。本文将详细介绍BP神经网络的算法过程,包括网络结构、激活函数、训练过程、反向传播算法、权重更新策略等。
- 网络结构
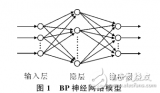
BP神经网络由输入层、隐藏层和输出层组成,每层包含若干神经元。输入层的神经元数量与问题的特征维度相同,输出层的神经元数量与问题的输出维度相同。隐藏层的数量和每层的神经元数量可以根据问题的复杂度和数据量进行调整。
1.1 输入层
输入层是BP神经网络的第一层,负责接收外部输入信号。输入层的神经元数量与问题的特征维度相同,每个神经元接收一个输入信号。
1.2 隐藏层
隐藏层是BP神经网络的中间层,负责对输入信号进行非线性变换和特征提取。隐藏层的数量可以根据问题的复杂度进行调整,通常设置1到3层。每层隐藏层的神经元数量可以根据数据量和问题规模进行调整。
1.3 输出层
输出层是BP神经网络的最后一层,负责生成预测结果。输出层的神经元数量与问题的输出维度相同,每个神经元生成一个预测值。
- 激活函数
激活函数是BP神经网络中神经元的非线性变换函数,用于引入非线性特性,提高网络的表达能力。常用的激活函数包括Sigmoid函数、Tanh函数、ReLU函数等。
2.1 Sigmoid函数
Sigmoid函数是一种常用的激活函数,其数学表达式为:
f(x) = 1 / (1 + exp(-x))
Sigmoid函数的输出范围在(0, 1)之间,具有平滑、连续的特点,适用于二分类问题。
2.2 Tanh函数
Tanh函数是Sigmoid函数的变体,其数学表达式为:
f(x) = (exp(x) - exp(-x)) / (exp(x) + exp(-x))
Tanh函数的输出范围在(-1, 1)之间,相对于Sigmoid函数,Tanh函数在x=0附近的变化更加陡峭,适用于多分类问题。
2.3 ReLU函数
ReLU(Rectified Linear Unit)函数是一种非线性激活函数,其数学表达式为:
f(x) = max(0, x)
ReLU函数在x>0时输出x,x<0时输出0。ReLU函数具有计算简单、收敛速度快的特点,广泛应用于深度学习中。
- 训练过程
BP神经网络的训练过程包括前向传播和反向传播两个阶段。
3.1 前向传播
前向传播是BP神经网络从输入层到输出层的信号传递过程。在前向传播过程中,输入信号经过每层神经元的加权求和和激活函数变换,最终生成预测结果。
具体步骤如下:
- 初始化输入层神经元的输入值。
- 对于每一层神经元,计算加权求和:net = w * x + b,其中w为权重矩阵,x为输入向量,b为偏置项。
- 对加权求和的结果应用激活函数,得到该层神经元的输出值。
- 将当前层的输出值作为下一层的输入值,重复步骤2-3,直到输出层。
3.2 反向传播
反向传播是BP神经网络从输出层到输入层的误差传递过程。在反向传播过程中,根据预测结果和真实值计算误差,并通过梯度下降算法更新网络权重。
具体步骤如下:
- 计算输出层的误差:E = (y - t),其中y为预测结果,t为真实值。
- 对输出层的误差应用激活函数的导数,得到输出层的梯度:dE = E * f'(net),其中f'(net)为激活函数的导数。
- 对于每一层神经元,从后向前计算梯度和误差:
a. 计算当前层的误差:delta = dE * w^T,其中w^T为上一层权重矩阵的转置。
b. 计算当前层的梯度:dW = x * delta,其中x为当前层的输入向量。 - 更新网络权重:W = W - alpha * dW,其中alpha为学习率。
-
信号处理
+关注
关注
48文章
999浏览量
103194 -
BP神经网络
+关注
关注
2文章
115浏览量
30532 -
非线性
+关注
关注
1文章
208浏览量
23060 -
神经元
+关注
关注
1文章
363浏览量
18436
发布评论请先 登录
相关推荐




 bp神经网络算法过程包括
bp神经网络算法过程包括











评论