BP神经网络算法,即反向传播神经网络算法,是一种常用的多层前馈神经网络训练算法。它通过反向传播误差来调整网络的权重和偏置,从而实现对输入数据的分类或回归。下面详细介绍BP神经网络算法的基本流程。
- 初始化网络参数
在BP神经网络算法中,首先需要初始化网络的参数,包括权重和偏置。权重是连接神经元之间的系数,偏置是神经元的阈值。权重和偏置的初始值通常设置为小的随机数,以避免对称性问题。
1.1 随机初始化权重
权重的初始化是BP神经网络算法的关键步骤之一。权重的初始值通常设置为小的随机数,例如在[-0.1, 0.1]范围内的随机数。权重的初始化方法有多种,如均匀分布、正态分布等。权重的初始化方法会影响网络的收敛速度和性能。
1.2 初始化偏置
偏置的初始化通常设置为0或小的随机数。偏置的值对网络的收敛速度和性能也有一定的影响。
- 前向传播
前向传播是BP神经网络算法的核心步骤之一。在前向传播过程中,输入数据通过隐藏层和输出层进行计算,得到网络的输出值。
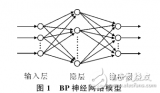
2.1 输入层
输入层是BP神经网络的第一层,负责接收输入数据。输入层的神经元数量与输入数据的特征数量相同。
2.2 隐藏层
隐藏层是BP神经网络的中间层,负责提取输入数据的特征。隐藏层的神经元数量可以根据问题的复杂度和数据量进行调整。隐藏层的激活函数通常使用Sigmoid函数、Tanh函数或ReLU函数等。
2.3 输出层
输出层是BP神经网络的最后一层,负责生成网络的输出值。输出层的神经元数量与问题的输出类别数量相同。输出层的激活函数通常使用Softmax函数或线性函数等。
- 计算误差
在前向传播过程中,网络的输出值与实际值之间存在误差。计算误差是BP神经网络算法的关键步骤之一。
3.1 误差函数
误差函数是衡量网络输出值与实际值之间差异的函数。常用的误差函数有均方误差函数(MSE)、交叉熵误差函数(Cross-Entropy)等。误差函数的选择取决于问题的类型和需求。
3.2 误差反向传播
误差反向传播是BP神经网络算法的核心步骤之一。在误差反向传播过程中,误差从输出层反向传播到输入层,通过链式法则计算每个权重和偏置对误差的贡献。
3.2.1 计算输出层的误差梯度
在输出层,误差梯度可以通过误差函数的导数计算得到。例如,对于均方误差函数,误差梯度为:
∂E/∂o = (o - t)
其中,o表示输出值,t表示实际值。
3.2.2 计算隐藏层的误差梯度
在隐藏层,误差梯度可以通过链式法则计算得到。对于第j个神经元,其误差梯度为:
∂E/∂zj = ∂E/∂oj * ∂oj/∂zj
其中,zj表示第j个神经元的输入值,oj表示第j个神经元的输出值。
3.2.3 更新权重和偏置
根据误差梯度,可以使用梯度下降法或其他优化算法更新网络的权重和偏置。权重和偏置的更新公式为:
w_new = w_old - α * ∂E/∂w
b_new = b_old - α * ∂E/∂b
其中,w表示权重,b表示偏置,α表示学习率。
- 迭代训练
BP神经网络算法通常需要多次迭代训练,以优化网络的性能。在每次迭代中,都需要进行前向传播、计算误差、误差反向传播和更新权重偏置等步骤。
4.1 学习率调整
学习率是BP神经网络算法中的一个重要参数,它决定了权重和偏置更新的幅度。学习率过大可能导致网络训练不稳定,学习率过小可能导致训练时间过长。在训练过程中,可以根据网络的性能调整学习率。
4.2 早停法
早停法是一种防止过拟合的方法。在训练过程中,可以使用验证集评估网络的性能。当验证集的性能不再提高时,可以提前停止训练,以避免过拟合。
- 模型评估
在训练完成后,需要对模型进行评估,以验证其性能。常用的评估指标有准确率、召回率、F1分数等。评估指标的选择取决于问题的需求和类型。
-
数据
+关注
关注
8文章
7134浏览量
89467 -
参数
+关注
关注
11文章
1859浏览量
32396 -
BP神经网络
+关注
关注
2文章
115浏览量
30597 -
神经元
+关注
关注
1文章
363浏览量
18499
发布评论请先 登录
相关推荐




 bp神经网络算法的基本流程包括哪些
bp神经网络算法的基本流程包括哪些











评论