前馈神经网络的基本结构和常见激活函数

引言

前馈神经网络（Feedforward Neural Network, FNN）是人工神经网络中最基本且广泛应用的一种结构，其结构简单、易于理解，是深度学习领域中的基石。FNN通过多层节点之间的连接和激活函数的非线性变换，能够学习和模拟复杂的函数映射，从而解决各种监督学习任务。本文将详细阐述前馈神经网络的基本结构，包括其组成层、权重和偏置、激活函数等，并介绍几种常见的激活函数及其特性。

一、前馈神经网络的基本结构

前馈神经网络是一种有向无环图结构，数据从输入层开始，通过隐藏层（可能有多层），最终到达输出层，整个过程中信息只能单向流动，不能反向传播。其基本结构包括输入层、隐藏层和输出层。

1. 输入层（Input Layer）

输入层是神经网络的第一层，负责接收外部输入数据。输入层的神经元数量通常与输入数据的特征数相同，每个神经元对应一个输入特征。输入层不对数据进行任何处理，只是将数据传递给下一层。

2. 隐藏层（Hidden Layer）

隐藏层位于输入层和输出层之间，是神经网络的核心部分。隐藏层可以有一层或多层，每层包含若干神经元。每个神经元都与前一层的所有神经元相连接，通过权重和偏置进行加权求和，并通过激活函数进行非线性变换。隐藏层的主要作用是对输入数据进行特征提取和模式识别，通过多层隐藏层的叠加，可以学习到更加复杂的特征表示。

3. 输出层（Output Layer）

输出层是神经网络的最后一层，负责产生最终的输出结果。输出层的神经元数量取决于具体的任务需求，如回归任务可能只有一个输出神经元，分类任务则根据类别数设置相应的神经元数。输出层同样使用激活函数进行非线性变换，以得到适合任务需求的输出结果。

4. 权重和偏置（Weights and Biases）

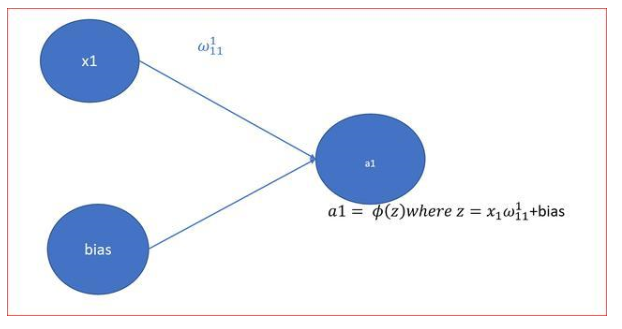
权重和偏置是神经网络中的可学习参数，用于调整神经元之间的连接强度和激活函数的输出。权重表示连接强度，决定了前一层神经元对后一层神经元的影响程度；偏置是一个常数项，用于调整激活函数的输出范围。在训练过程中，权重和偏置会不断更新，以最小化损失函数，提高模型的预测性能。

二、前馈神经网络的常见激活函数

激活函数是神经网络中非常重要的组成部分，它向网络引入非线性特性，使得网络能够学习和模拟复杂的函数映射。常见的激活函数包括Sigmoid、Tanh、ReLU等。

1. Sigmoid函数

Sigmoid函数是一种经典的激活函数，其数学表达式为：

[ sigma(x) = frac{1}{1 + e^{-x}} ]

Sigmoid函数将输入值映射到(0,1)区间内，输出值可以解释为概率或置信度。然而，Sigmoid函数存在梯度消失和梯度爆炸的问题，当输入值远离0时，其梯度趋近于0，导致在反向传播过程中权重更新缓慢甚至停滞。此外，Sigmoid函数的输出均值不为0，这会导致后一层的神经元输入出现偏移，影响模型的收敛速度。

2. Tanh函数

Tanh函数是Sigmoid函数的改进版，其数学表达式为：

[ tanh(x) = frac{ex - e{-x}}{ex + e{-x}} ]

Tanh函数将输入值映射到(-1,1)区间内，输出值以0为中心，这有助于加快模型的收敛速度。然而，Tanh函数同样存在梯度消失的问题，当输入值远离0时，其梯度也会趋近于0。

3. ReLU函数

ReLU（Rectified Linear Unit）函数是目前最常用的激活函数之一，其数学表达式为：

[ text{ReLU}(x) = max(0, x) ]

ReLU函数具有计算简单、收敛速度快、缓解梯度消失等优点。当输入值大于0时，ReLU函数保持线性增长，这有助于保持梯度的稳定性；当输入值小于等于0时，ReLU函数输出为0，这有助于增加网络的稀疏性，减少计算量。然而，ReLU函数也存在死亡ReLU（Dead ReLU）问题，即当神经元输入长时间小于0时，该神经元将不再被激活，导致梯度无法传递。

4. 其他激活函数

除了上述三种常见的激活函数外，还有许多其他激活函数被广泛应用于神经网络中，如Leaky ReLU、PReLU、ELU、SELU等。这些激活函数在ReLU函数的基础上进行了改进和优化，旨在解决ReLU函数存在的问题，提高神经网络的性能。

三、前馈神经网络的训练过程

前馈神经网络的训练过程主要包括前向传播、损失函数计算、反向传播和权重更新四个步骤。

1. 前向传播

在前向传播过程中，输入数据首先进入输入层，然后通过权重和偏置传递到隐藏层。隐藏层中的神经元对输入进行加权求和，并通过激活函数进行非线性变换。最后，输出层接收到经过隐藏层处理的信号，并产生最终的输出结果。

2. 损失函数计算

损失函数用于衡量模型预测值与实际值之间的差异。在训练过程中，我们需要定义一个合适的损失函数来计算模型的预测误差。常见的损失函数包括均方误差（MSE）用于回归任务、交叉熵损失（Cross-Entropy Loss）用于分类任务等。

3. 反向传播

反向传播是一种高效计算损失函数梯度的算法。在反向传播过程中，我们从输出层开始逐层计算损失函数关于权重的梯度，并将这些梯度反向传播到每一层。通过链式法则和梯度下降优化算法来更新权重和偏置以最小化损失函数。

4. 权重更新

在权重更新过程中我们使用优化算法（如SGD、Adam、RMSProp等）来更新权重和偏置。优化算法通过计算梯度并应用学习率来调整权重和偏置的值以最小化损失函数。

四、前馈神经网络的应用与前景

前馈神经网络由于其结构简单、易于实现和训练等优点被广泛应用于各种领域如图像识别、语音识别、自然语言处理、推荐系统等。随着深度学习技术的不断发展和完善前馈神经网络将继续在各个领域发挥重要作用并推动科学技术的进步和发展。

结论

前馈神经网络作为人工神经网络中最基本且广泛应用的结构之一其基本结构和常见激活函数对于理解和应用深度学习技术具有重要意义。通过深入了解和掌握前馈神经网络的基本原理和训练方法我们可以更好地利用这一工具来解决实际问题并推动科学技术的进步和发展。