非线性电路的基本特点是什么

非线性电路是一类具有非线性特性的电路，其输出与输入之间的关系不是线性的。非线性电路在电子技术、通信技术、自动控制等领域有着广泛的应用。本文将详细分析非线性电路的基本特点。

1. 非线性电路的定义

非线性电路是指电路中的元件或电路本身具有非线性特性，即输入与输出之间的关系不是线性的。在非线性电路中，元件的电压、电流或功率与时间的关系不是简单的正比关系，而是满足某种非线性函数关系。

2. 非线性电路的分类

非线性电路可以根据其非线性特性的来源进行分类，主要包括以下几种：

2.1 电阻非线性电路

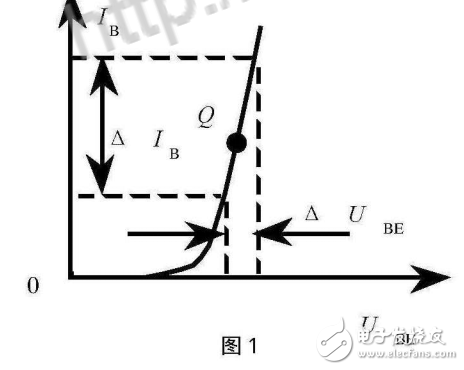
电阻非线性电路是指电路中的电阻元件具有非线性特性，如二极管、晶体管、变容二极管等。这些元件的电压-电流关系不是简单的线性关系，而是满足某种非线性函数关系。

2.2 电容非线性电路

电容非线性电路是指电路中的电容元件具有非线性特性，如变容二极管、非线性电容等。这些元件的电荷-电压关系不是简单的线性关系，而是满足某种非线性函数关系。

2.3 电感非线性电路

电感非线性电路是指电路中的电感元件具有非线性特性，如磁芯电感、非线性电感等。这些元件的磁通-电流关系不是简单的线性关系，而是满足某种非线性函数关系。

2.4 传输线非线性电路

传输线非线性电路是指电路中的传输线具有非线性特性，如非线性传输线、非线性耦合器等。这些元件的传输特性不是简单的线性关系，而是满足某种非线性函数关系。

3. 非线性电路的数学模型

非线性电路的数学模型主要包括以下几种：

3.1 微分方程模型

微分方程模型是描述非线性电路中电压、电流等物理量随时间变化的数学模型。根据电路的拓扑结构和元件特性，可以建立相应的微分方程，如一阶微分方程、二阶微分方程等。

3.2 代数方程模型

代数方程模型是描述非线性电路中电压、电流等物理量之间关系的数学模型。根据电路的拓扑结构和元件特性，可以建立相应的代数方程，如非线性代数方程、非线性方程组等。

3.3 状态空间模型

状态空间模型是描述非线性电路中状态变量随时间变化的数学模型。状态变量可以是电压、电流等物理量，也可以是电路的内部变量。状态空间模型可以用于分析电路的稳定性、频率响应等特性。

4. 非线性电路的分析方法

非线性电路的分析方法主要包括以下几种：

4.1 线性化方法

线性化方法是将非线性电路近似为线性电路进行分析的方法。通过在工作点附近进行线性化，可以得到线性电路的参数，如电阻、电容、电感等。线性化方法适用于非线性程度较小的电路。

4.2 迭代法

迭代法是通过迭代求解非线性电路的数学模型的方法。首先假设一个初始解，然后根据数学模型进行迭代计算，逐步逼近实际解。迭代法适用于非线性程度较大的电路。

4.3 符号计算法

符号计算法是利用计算机符号计算软件对非线性电路的数学模型进行求解的方法。符号计算法可以自动推导电路的解析解或数值解，适用于复杂的非线性电路。

4.4 蒙特卡洛法

蒙特卡洛法是通过随机抽样对非线性电路进行统计分析的方法。通过大量的随机抽样，可以得到电路的统计特性，如均值、方差等。蒙特卡洛法适用于具有随机性的非线性电路。

5. 非线性电路的稳定性

非线性电路的稳定性是指电路在受到扰动后能否恢复到稳定工作状态的能力。非线性电路的稳定性分析主要包括以下几种方法：

5.1 李雅普诺夫方法

李雅普诺夫方法是利用李雅普诺夫函数对非线性电路的稳定性进行分析的方法。通过构造合适的李雅普诺夫函数，可以判断电路的稳定性。

5.2 奈奎斯特判据

奈奎斯特判据是利用奈奎斯特图对非线性电路的稳定性进行分析的方法。通过绘制奈奎斯特图，可以判断电路的稳定性。

5.3 伯德图法

伯德图法是利用伯德图对非线性电路的频率响应进行分析的方法。通过绘制伯德图，可以判断电路的稳定性。