减小系统稳态误差是控制系统设计中的一个重要目标,它关系到系统的精度和性能。本文将介绍减小系统稳态误差的方法和策略,包括开环增益、PID控制器、前馈控制、状态观测器、自适应控制、鲁棒控制、智能控制等。
- 开环增益
开环增益是控制系统中最基本的参数之一,它直接影响系统的稳态误差。开环增益越大,系统的稳态误差越小。但是,过大的开环增益会导致系统的稳定性和抗干扰能力下降。因此,在设计控制系统时,需要合理选择开环增益,以达到减小稳态误差和保证系统稳定性的平衡。
1.1 开环增益的定义
开环增益是指在没有反馈作用的情况下,输入信号与输出信号之间的比例关系。在数学上,开环增益可以表示为:
G_{OL} = frac{V_{out}}{V_{in}}
其中,V_{in} 是输入信号,V_{out} 是输出信号。
1.2 开环增益对稳态误差的影响
根据控制系统的基本原理,稳态误差可以表示为:
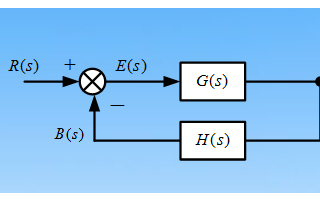
e_{ss} = frac{r - y}{1 + G_{OL} cdot H}
其中,r 是参考输入,y 是实际输出,H 是反馈增益。从上式可以看出,开环增益越大,稳态误差越小。
1.3 开环增益的选择
在实际工程中,开环增益的选择需要考虑多种因素,如系统的稳定性、抗干扰能力、成本等。一般来说,可以通过以下方法来选择开环增益:
- 根据系统的性能要求,确定稳态误差的允许范围。
- 通过仿真或实验,测量系统的开环增益和稳态误差之间的关系。
- 根据稳定性分析,确定开环增益的最大值,以避免系统的不稳定。
- 综合考虑成本、可靠性等因素,选择一个合适的开环增益。
- PID控制器
PID控制器是一种常见的反馈控制器,它通过比例(P)、积分(I)和微分(D)三个环节来调整系统的输出,以达到减小稳态误差的目的。
2.1 PID控制器的基本原理
PID控制器的基本结构可以表示为:
u(t) = K_p e(t) + K_i int_{0}^{t} e(tau) dtau + K_d frac{de(t)}{dt}
其中,u(t) 是控制器的输出,e(t) 是误差信号,K_p、K_i 和 K_d 分别是比例、积分和微分增益。
2.2 PID控制器对稳态误差的影响
PID控制器可以有效地减小系统的稳态误差。具体来说:
- 比例环节可以快速响应误差信号,减小误差的大小。
- 积分环节可以消除稳态误差,提高系统的精度。
- 微分环节可以预测误差的变化趋势,提前调整控制器的输出,减小超调和振荡。
2.3 PID控制器的设计方法
PID控制器的设计方法有很多,如经验法、极点配置法、最小方差法等。在实际工程中,可以根据系统的特点和性能要求,选择合适的设计方法。一般来说,设计PID控制器需要考虑以下步骤:
- 确定系统的开环传递函数或模型。
- 选择合适的控制规律,如比例控制、比例-积分控制、比例-微分控制或比例-积分-微分控制。
- 通过仿真或实验,调整PID参数,以达到减小稳态误差和满足性能要求的目的。
- 进行稳定性分析和抗干扰能力评估,确保控制器的可靠性。
- 前馈控制
前馈控制是一种基于输入信号预测系统输出的控制方法。通过引入前馈环节,可以提前调整系统的输出,减小稳态误差。
3.1 前馈控制的基本原理
前馈控制的基本结构可以表示为:
u(t) = G_f r(t) + G_c e(t)
其中,G_f 是前馈增益,G_c 是反馈增益。
3.2 前馈控制对稳态误差的影响
前馈控制可以有效地减小系统的稳态误差。具体来说:
- 前馈环节可以根据输入信号的变化趋势,提前调整系统的输出。
- 前馈控制可以消除系统的纯积分误差,提高系统的精度。
- 前馈控制可以减少系统的超调和振荡,提高系统的稳定性。
-
控制系统
+关注
关注
41文章
6604浏览量
110576 -
反馈控制器
+关注
关注
0文章
6浏览量
5524 -
稳态误差
+关注
关注
0文章
8浏览量
2094
发布评论请先 登录
相关推荐




 减小系统稳态误差可采用什么环节
减小系统稳态误差可采用什么环节










评论