频率响应是电子系统、信号处理和通信领域中一个非常重要的概念。它描述了系统对不同频率信号的响应特性。频率响应分析可以帮助我们了解系统的性能,优化系统设计,提高信号处理质量。
1. 频率响应的定义
频率响应(Frequency Response)是指一个线性时不变(LTI)系统对不同频率信号的响应。在数学上,频率响应可以通过系统的传递函数(Transfer Function)来描述。传递函数是输入信号与输出信号之间的比值,通常表示为复数函数,包含了幅度和相位信息。
2. 幅度响应与相位响应
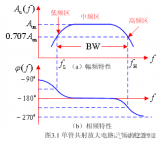
频率响应通常由幅度响应和相位响应两部分组成:
- 幅度响应 :表示系统对不同频率信号的增益或衰减程度。通常以分贝(dB)为单位,描述为 ( |H(f)| ),其中 ( H(f) ) 是传递函数的幅度。
- 相位响应 :表示系统对不同频率信号的相位变化。相位响应通常以弧度或度为单位,描述为 ( angle H(f) )。
3. 频率响应的数学表达
对于一个线性时不变系统,其频率响应可以通过傅里叶变换来计算。给定一个时域信号 ( x(t) ),其傅里叶变换为 ( X(f) ),系统的频率响应 ( H(f) ) 与输出信号的傅里叶变换 ( Y(f) ) 之间的关系为:
[ Y(f) = H(f) cdot X(f) ]
4. 频率响应的类型
根据系统的特性,频率响应可以分为以下几类:
- 低通滤波器 :允许低频信号通过,抑制高频信号。
- 高通滤波器 :允许高频信号通过,抑制低频信号。
- 带通滤波器 :只允许特定频率范围内的信号通过。
- 带阻滤波器 :抑制特定频率范围内的信号,允许其他频率的信号通过。
5. 频率响应的测量方法
测量频率响应通常涉及以下几个步骤:
5.1 激励信号的生成
首先,需要生成一个包含所需频率范围的信号。这可以是正弦波、方波或脉冲信号等。
5.2 信号的输入与输出
将激励信号输入到待测系统,同时记录系统的输出信号。
5.3 信号的傅里叶变换
对输入和输出信号进行傅里叶变换,得到它们的频域表示。
5.4 计算频率响应
通过比较输入和输出信号的频域表示,计算系统的频率响应。具体计算公式为:
[ H(f) = frac{Y(f)}{X(f)} ]
5.5 分析幅度和相位响应
从计算得到的频率响应中,提取幅度响应和相位响应,并进行分析。
6. 测量工具与设备
测量频率响应通常需要以下工具和设备:
7. 频率响应的应用
频率响应分析在许多领域都有重要应用,包括:
8. 频率响应的优化
为了提高系统性能,可能需要对频率响应进行优化。这通常涉及到调整系统的参数,如滤波器的截止频率、增益等。
-
信号处理
+关注
关注
48文章
1034浏览量
103324 -
电子系统
+关注
关注
0文章
422浏览量
31196 -
频率响应
+关注
关注
1文章
101浏览量
18339 -
函数
+关注
关注
3文章
4338浏览量
62773
发布评论请先 登录
相关推荐
哪些参数会影响麦克风频率响应?哪种评估频率响应的最佳方法?
频率响应基本概念
频率响应是什么意思_频率响应特性

频率响应介绍_频率响应概念

音响频率响应多少好_频率响应大好还是小好
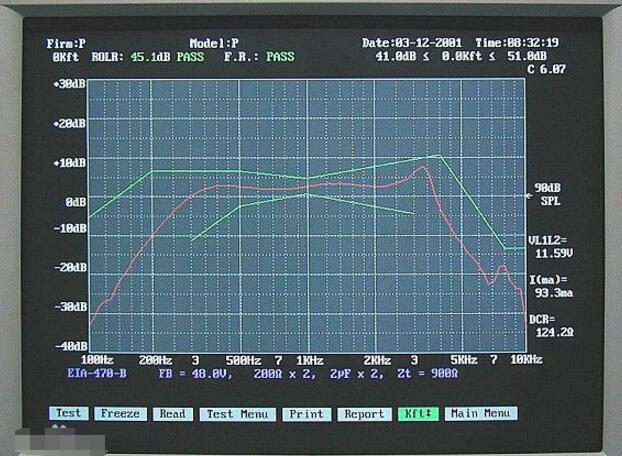




 频率响应的基本概念与测量方法
频率响应的基本概念与测量方法












评论