拉普拉斯变换在工程数学中是一种重要的积分变换,其作用及意义主要体现在以下几个方面:
作用
- 简化求解过程 :
- 信号处理与分析 :
- 分析信号频谱特性 :在信号处理中,拉普拉斯变换可以将时域上的信号转换成复频域上的信号,从而方便地分析信号的频谱特性。这对于信号的滤波、调制等处理提供了有力的工具。
- 滤波器设计 :在滤波器设计中,可以通过将滤波器的传递函数转换成在复频率域上的表达式,从而分析滤波器的特性,并进行滤波器设计。
- 电路分析 :
- 电路问题求解 :在电路理论中,拉普拉斯变换被用于分析和设计线性电路。通过将电路中的电压、电流等物理量转换为复频域中的函数,并利用复频域中的分析方法求解电路问题,可以使得电路分析更加简便。
- 解决边界值问题 :
- 复杂物理问题求解 :拉普拉斯变换在解决边界值问题(如热传导、振动等)中也具有重要的作用。通过将微分方程转换为代数方程,可以更容易地求解这些复杂的物理问题。
意义
- 提供强有力的工具 :拉普拉斯变换将时域中的函数转换到复频域中进行分析,为处理复杂的数学问题和工程问题提供了一种强有力的工具。这种变换不仅使得求解过程更加直观和简洁,而且为处理一些在时域中难以直接求解的问题提供了可能。
- 推动领域发展 :拉普拉斯变换在控制论、信号处理、电路分析等领域中的广泛应用,推动了这些领域的发展和进步。通过拉普拉斯变换,工程师和科学家能够更好地理解和处理微分方程、信号和系统,从而设计出更加高效和可靠的系统。
- 促进跨学科研究 :拉普拉斯变换不仅在数学领域具有重要地位,而且在物理学、工程学、经济学等多个领域中也得到了广泛应用。这种跨学科的应用促进了不同领域之间的交流和合作,推动了科学研究的整体进步。
综上所述,拉普拉斯变换在工程数学和多个科学领域中具有重要的作用和意义,它是一种不可或缺的数学工具和分析方法。
声明:本文内容及配图由入驻作者撰写或者入驻合作网站授权转载。文章观点仅代表作者本人,不代表电子发烧友网立场。文章及其配图仅供工程师学习之用,如有内容侵权或者其他违规问题,请联系本站处理。
举报投诉
-
滤波器
+关注
关注
161文章
7902浏览量
179296 -
信号处理
+关注
关注
48文章
1046浏览量
103475 -
函数
+关注
关注
3文章
4350浏览量
63141 -
拉普拉斯变换
+关注
关注
1文章
32浏览量
10206
发布评论请先 登录
相关推荐
拉普拉斯、傅里叶及各种变换的原理和意义
电路和电力电子学里经常说的用的拉普拉斯变换,傅里叶变换自己断断续续所接触的时间不少了但一直弄不明白原理和它们的意义公式可以记忆,但是想弄懂它们的原理和
发表于 10-24 13:25
拉普拉斯变换及其逆变换表拉普拉斯变换及其逆变换表
有些情形下一个实变量函数在实数域中进行一些运算并不容易,但若将实变量函数作拉普拉斯变换,并在复数域中作各种运算,再将运算结果作拉普拉斯反变换来求得实数域中的相应结果,在经典控制理论中,
发表于 12-05 18:30
•26w次阅读

拉普拉斯变换的意义
拉普拉斯变换的意义 拉普拉斯变换是微积分中的一种重要方法,用于将时间域函数转换为复平面的频域函数。它是工程和科学中常用的一种数学工具,尤其是
拉普拉斯变换公式
拉普拉斯变换公式 拉普拉斯变换公式是数学中极其重要的一种变换方式,它的应用领域非常广泛,包括在信号处理、控制论、微分方程、电路分析和量子力




 拉普拉斯变换的作用及意义
拉普拉斯变换的作用及意义
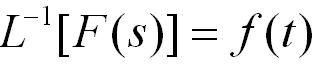
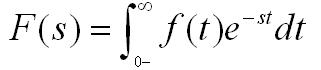










评论