巴特沃斯二阶滤波器工作原理是什么

巴特沃斯二阶滤波器是一种常用的数字滤波器，它具有平滑的频率响应和良好的滤波特性。

1. 巴特沃斯二阶滤波器的数学模型

巴特沃斯二阶滤波器是一种无限脉冲响应（IIR）滤波器，其数学模型可以用差分方程表示。对于一个二阶巴特沃斯低通滤波器，其差分方程如下：

y[n] = α * x[n] + (1 - α) * y[n-1] - α * y[n-2]

其中，x[n]是输入信号，y[n]是输出信号，α是滤波器的参数，n是离散时间索引。α的取值范围为0到1，它决定了滤波器的截止频率和滤波特性。

巴特沃斯二阶滤波器的频率响应可以用以下公式表示：

H(ω) = Y(ω) / X(ω) = 1 / (1 + α * (2 * cos(ω) - 1))

其中，ω是归一化频率，表示输入信号频率与滤波器截止频率的比值。Y(ω)和X(ω)分别是输入信号和输出信号的傅里叶变换。

2. 巴特沃斯二阶滤波器的设计方法

巴特沃斯二阶滤波器的设计主要包括确定滤波器的参数α和截止频率。以下是设计巴特沃斯二阶滤波器的步骤：

2.1 确定滤波器的阶数和类型

根据滤波器的设计要求，确定滤波器的阶数和类型。巴特沃斯二阶滤波器是一种低通滤波器，可以用于滤除高频噪声。如果需要其他类型的滤波器，如高通、带通或带阻滤波器，可以通过对低通滤波器进行适当的变换得到。

2.2 确定滤波器的截止频率

截止频率是滤波器的一个重要参数，它决定了滤波器对信号的滤波特性。截止频率可以根据信号的特性和应用场景来确定。一般来说，截止频率应该选择在信号的有用频带之外，以滤除不需要的高频成分。

2.3 计算滤波器的参数α

根据滤波器的阶数和截止频率，可以计算出滤波器的参数α。对于二阶巴特沃斯滤波器，α的计算公式如下：

α = 2 / (1 + sqrt(1 + (2 * π * 截止频率 / 采样频率)^2))

其中，采样频率是数字信号的采样率，π是圆周率。

2.4 验证滤波器的性能

设计完成后，需要对滤波器的性能进行验证。可以通过对滤波器的频率响应和相位响应进行分析，检查滤波器是否满足设计要求。此外，还可以通过实际信号的滤波效果来评估滤波器的性能。

3. 巴特沃斯二阶滤波器的性能指标

巴特沃斯二阶滤波器的性能指标主要包括以下几方面：

3.1 截止频率

截止频率是滤波器的一个重要参数，它决定了滤波器对信号的滤波特性。截止频率的选择应该根据信号的特性和应用场景来确定。

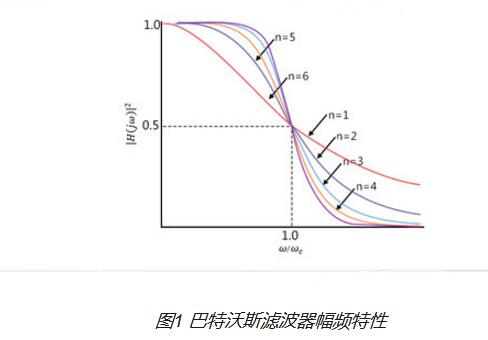
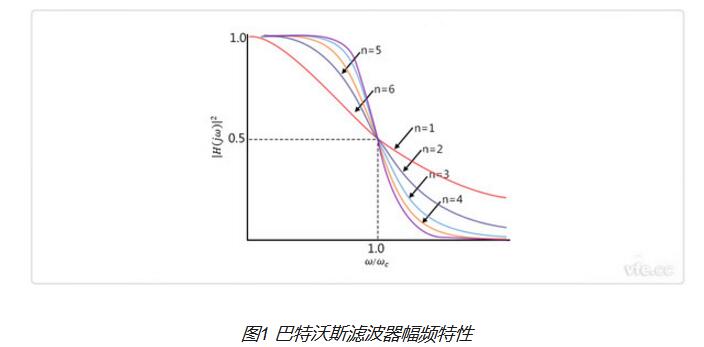
3.2 滤波器的幅度特性

巴特沃斯二阶滤波器的幅度特性是平滑的，没有尖锐的截止点。这使得巴特沃斯滤波器在实际应用中具有较好的性能，尤其是在需要平滑过渡的场合。

3.3 滤波器的相位特性

巴特沃斯二阶滤波器的相位特性是线性的，即相位随频率的变化是线性的。这使得滤波器在处理信号时，不会引入额外的相位失真。

3.4 滤波器的稳定性

巴特沃斯二阶滤波器是稳定的，即其输出信号不会随着输入信号的变化而发散。这使得巴特沃斯滤波器在实际应用中具有较好的稳定性。