在解释机器学习的基本概念的时候,我发现自己总是回到有限的几幅图中。以下是我认为最有启发性的条目列表。
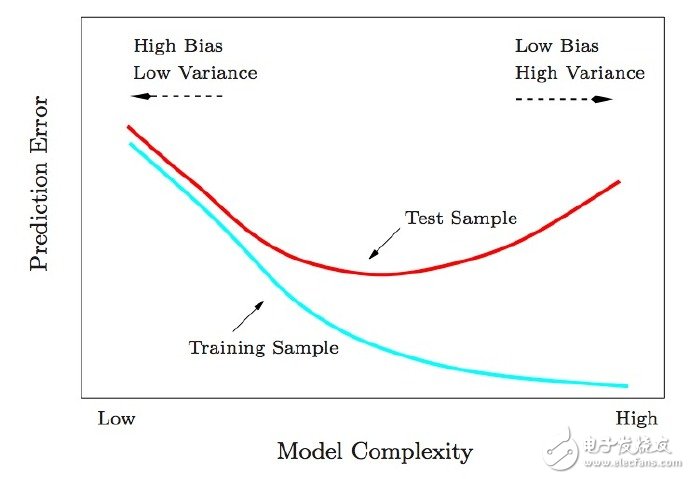
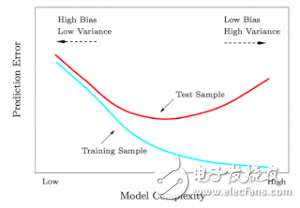
1. Test and training error: 为什么低训练误差并不总是一件好的事情呢:ESL 图2.11.以模型复杂度为变量的测试及训练错误函数。
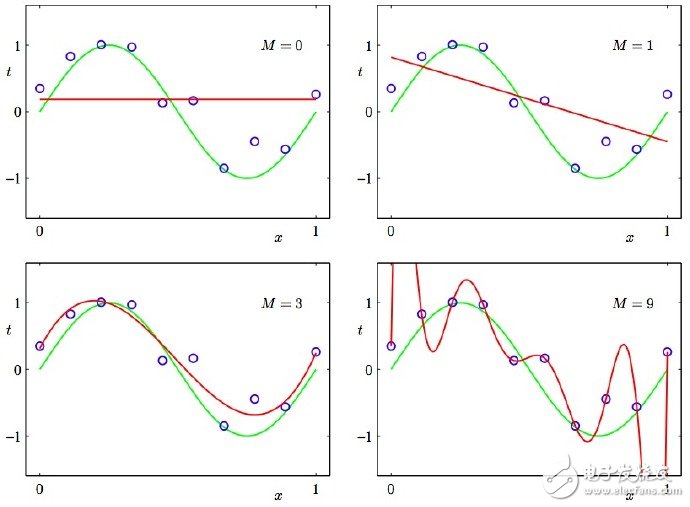
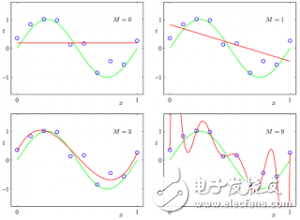
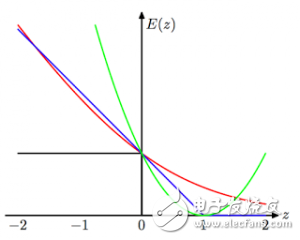
2. Under and overfitting: 低度拟合或者过度拟合的例子。PRML 图1.4.多项式曲线有各种各样的命令M,以红色曲线表示,由绿色曲线适应数据集后生成。
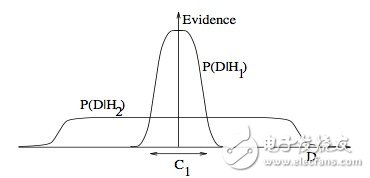
3. Occam’s razor
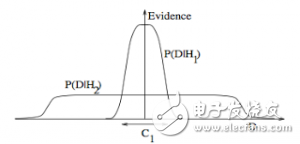
ITILA 图28.3.为什么贝叶斯推理可以具体化奥卡姆剃刀原理。这张图给了为什么复杂模型原来是小概率事件这个问题一个基本的直观的解释。水平轴代表了可能的数据集D空间。贝叶斯定理以他们预测的数据出现的程度成比例地反馈模型。这些预测被数据D上归一化概率分布量化。数据的概率给出了一种模型Hi,P(D|Hi)被称作支持Hi模型的证据。一个简单的模型H1仅可以做到一种有限预测,以P(D|H1)展示;一个更加强大的模型H2,举例来说,可以比模型H1拥有更加自由的参数,可以预测更多种类的数据集。这也表明,无论如何,H2在C1域中对数据集的预测做不到像H1那样强大。假设相等的先验概率被分配给这两种模型,之后数据集落在C1区域,不那么强大的模型H1将会是更加合适的模型。
4. Feature combinations:
(1)为什么集体相关的特征单独来看时无关紧要,这也是(2)线性方法可能会失败的原因。从Isabelle Guyon特征提取的幻灯片来看。
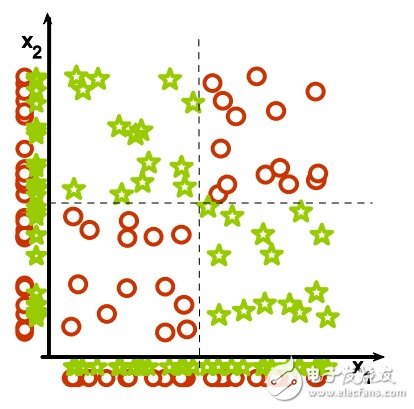
5. Irrelevant features:
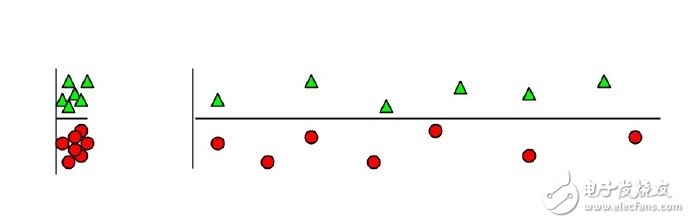
为什么无关紧要的特征会损害KNN,聚类,以及其它以相似点聚集的方法。左右的图展示了两类数据很好地被分离在纵轴上。右图添加了一条不切题的横轴,它破坏了分组,并且使得许多点成为相反类的近邻。
6. Basis functions
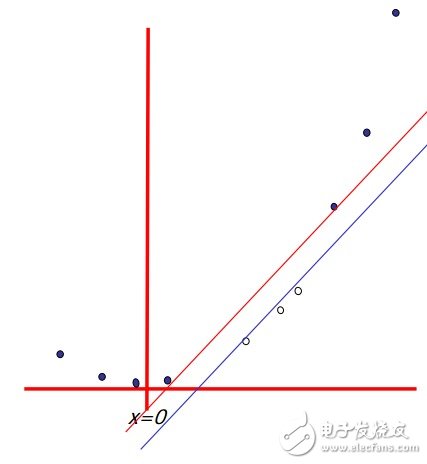
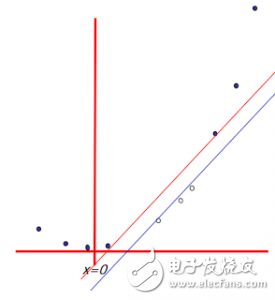
非线性的基础函数是如何使一个低维度的非线性边界的分类问题,转变为一个高维度的线性边界问题。Andrew Moore的支持向量机SVM(Support Vector Machine)教程幻灯片中有:一个单维度的非线性带有输入x的分类问题转化为一个2维的线性可分的z=(x,x^2)问题。
7. Discriminative vs. Generative:
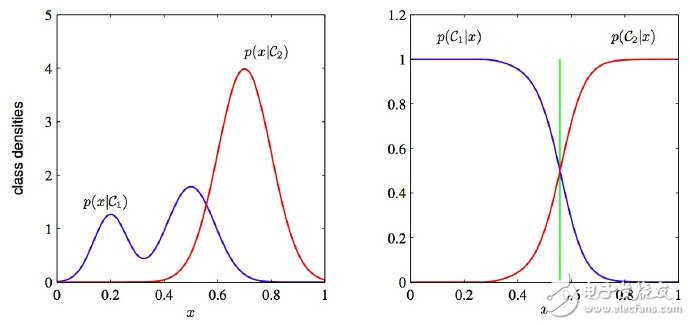
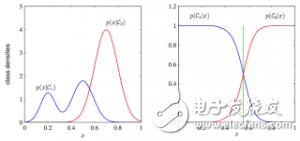
为什么判别式学习比产生式更加简单:PRML 图1.27.这两类方法的分类条件的密度举例,有一个单一的输入变量x(左图),连同相应的后验概率(右图)。注意到左侧的分类条件密度p(x|C1)的模式,在左图中以蓝色线条表示,对后验概率没有影响。右图中垂直的绿线展示了x中的决策边界,它给出了最小的误判率。
8. Loss functions:
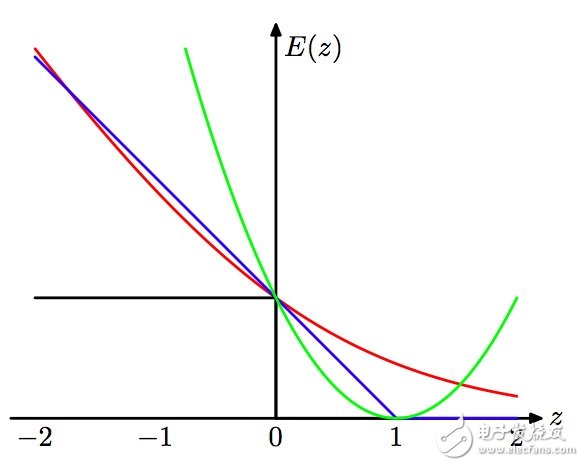
学习算法可以被视作优化不同的损失函数:PRML 图7.5. 应用于支持向量机中的“铰链”错误函数图形,以蓝色线条表示,为了逻辑回归,随着错误函数被因子1/ln(2)重新调整,它通过点(0,1),以红色线条表示。黑色线条表示误分,均方误差以绿色线条表示。
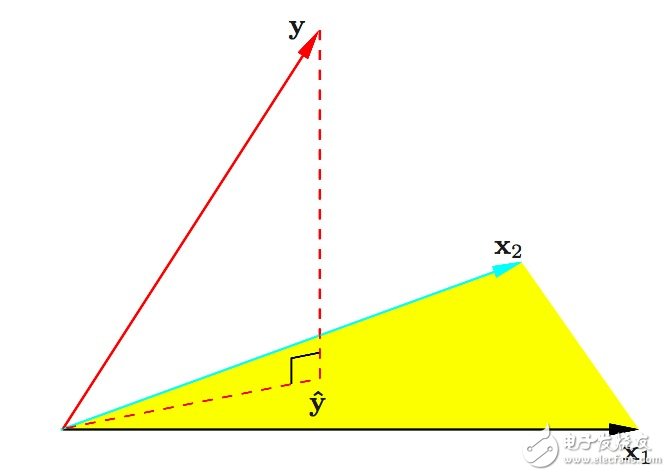
9. Geometry of least squares:
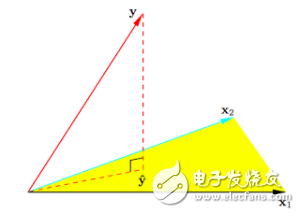
ESL 图3.2.带有两个预测的最小二乘回归的N维几何图形。结果向量y正交投影到被输入向量x1和x2所跨越的超平面。投影y^代表了最小二乘预测的向量。
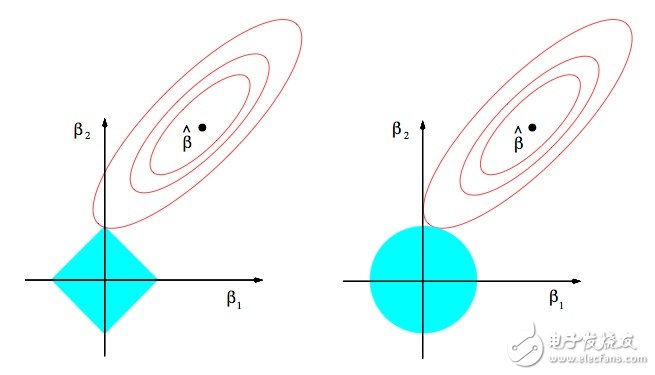
10. Sparsity:
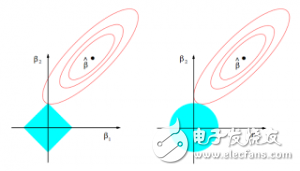
为什么Lasso算法(L1正规化或者拉普拉斯先验)给出了稀疏的解决方案(比如:带更多0的加权向量):ESL 图3.11.lasso算法的估算图像(左)以及岭回归算法的估算图像(右)。展示了错误的等值线以及约束函数。分别的,当红色椭圆是最小二乘误差函数的等高线时,实心的蓝色区域是约束区域|β1| + |β2| ≤ t以及β12 + β22 ≤ t2。
英文原文:
I find myself coming back to the same few pictures when explaining basic machine learning concepts. Below is a list I find most illuminating.
我发现自己在解释基本的机器学习概念时经常碰到少数相同的图片。下面列举了我认为最有启发性的图片。
1. Test and training error(测试和训练错误): Why lower training error is not always a good thing: ESL Figure 2.11. Test and training error as a function of model complexity.
2. Under and overfitting(欠拟合和过拟合): PRML Figure 1.4. Plots of polynomials having various orders M, shown as red curves, fitted to the data set generated by the green curve.
3. Occam’s razor(奥卡姆剃刀): ITILA Figure 28.3. Why Bayesian inference embodies Occam’s razor. This figure gives the basic intuition for why complex models can turn out to be less probable. The horizontal axis represents the space of possible data sets D. Bayes’ theorem rewards models in proportion to how much they predicted the data that occurred. These predictions are quantified by a normalized probability distribution on D. This probability of the data given model Hi, P (D | Hi), is called the evidence for Hi. A simple model H1 makes only a limited range of predictions, shown by P(D|H1); a more powerful model H2, that has, for example, more free parameters than H1, is able to predict a greater variety of data sets. This means, however, that H2 does not predict the data sets in region C1 as strongly as H1. Suppose that equal prior probabilities have been assigned to the two models. Then, if the data set falls in region C1, the less powerful model H1 will be the more probable model.
4. Feature combinations(Feature组合): (1) Why collectively relevant features may look individually irrelevant, and also (2) Why linear methods may fail. From Isabelle Guyon’s feature extraction slides.
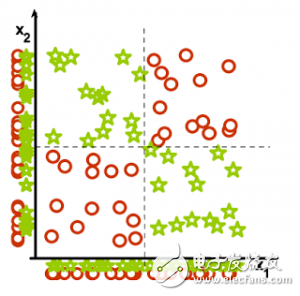
5. Irrelevant features(不相关特征): Why irrelevant features hurt kNN, clustering, and other similarity based methods. The figure on the left shows two classes well separated on the vertical axis. The figure on the right adds an irrelevant horizontal axis which destroys the grouping and makes many points nearest neighbors of the opposite class.
6. Basis functions(基函数): How non-linear basis functions turn a low dimensional classification problem without a linear boundary into a high dimensional problem with a linear boundary. From SVM tutorial slides by Andrew Moore: a one dimensional non-linear classification problem with input x is turned into a 2-D problem z=(x, x^2) that is linearly separable.
7. Discriminative vs. Generative(判别与生成): Why discriminative learning may be easier than generative: PRML Figure 1.27. Example of the class-conditional densities for two classes having a single input variable x (left plot) together with the corresponding posterior probabilities (right plot)。 Note that the left-hand mode of the class-conditional density p(x|C1), shown in blue on the left plot, has no effect on the posterior probabilities. The vertical green line in the right plot shows the decision boundary in x that gives the minimum misclassification rate.
8. Loss functions(损失函数): Learning algorithms can be viewed as optimizing different loss functions: PRML Figure 7.5. Plot of the ‘hinge’ error function used in support vector machines, shown in blue, along with the error function for logistic regression, rescaled by a factor of 1/ln(2) so that it passes through the point (0, 1), shown in red. Also shown are the misclassification error in black and the squared error in green.
9. Geometry of least squares(最小二乘的几何图形): ESL Figure 3.2. The N-dimensional geometry of least squares regression with two predictors. The outcome vector y is orthogonally projected onto the hyperplane spanned by the input vectors x1 and x2. The projection y? represents the vector of the least squares predictions.
10. Sparsity(稀疏性): Why Lasso (L1 regularization or Laplacian prior) gives sparse solutions (i.e. weight vectors with more zeros): ESL Figure 3.11. Estimation picture for the lasso (left) and ridge regression (right)。 Shown are contours of the error and constraint functions. The solid blue areas are the constraint regions |β1| + |β2| ≤ t and β12 + β22 ≤ t2, respectively, while the red ellipses are the contours of the least squares error function.
-
机器学习
+关注
关注
66文章
8406浏览量
132565
发布评论请先 登录
相关推荐
探讨机器学习与深度学习基本概念与运算过程




 什么是机器学习_十张图带你解析机器学习的基本概念
什么是机器学习_十张图带你解析机器学习的基本概念













评论