抖动基本概念
绝对抖动 (Absolute Jitter) 是一个衡量时间点的不确定性概念,参考为理想时钟的时间点,该相对偏差量可能表示为一个离散时间的随机变量。绝对抖动造成的时间点不确定性可能会对很多采样电路有影响,比如在数据时钟恢复电路 (CDR) 中,需要利用时钟沿对数据的中心和数据变化的沿进行采样,采样时钟的绝对抖动对于 CDR 的抖动容限有直接影响。周期抖动 (Period Jitter) 是一个衡量时间段不确定性的概念,定义为实际时钟和理想时钟的周期偏差,同样可以表示为离散事件随机变量,如下图 (图1) 所示:
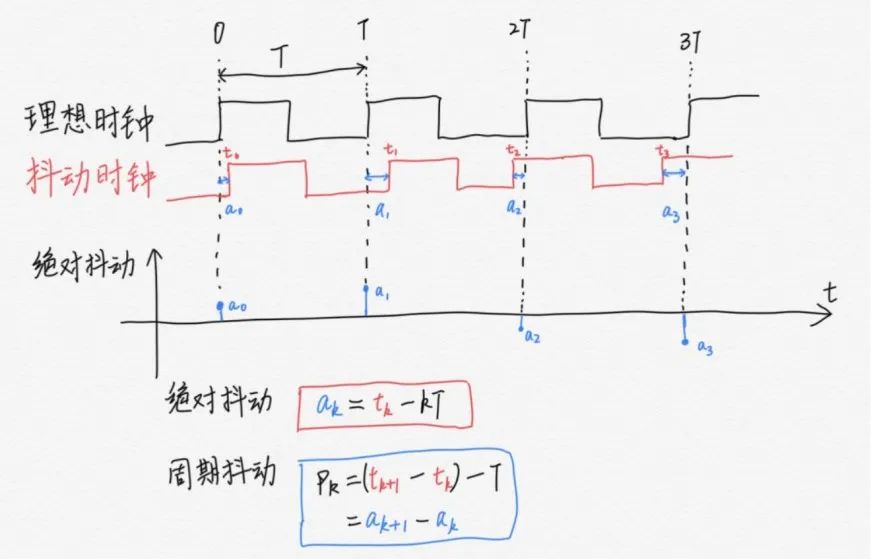
图1 周期抖动数据表
时钟 Clk 半速率采样非理想的数据 Data,如下图 (图2) 所示,如果时钟 Clk 偏离中间采样位置,该抖动会造成采样后数据的错误,且该抖动越大,数据的误码率就越高。
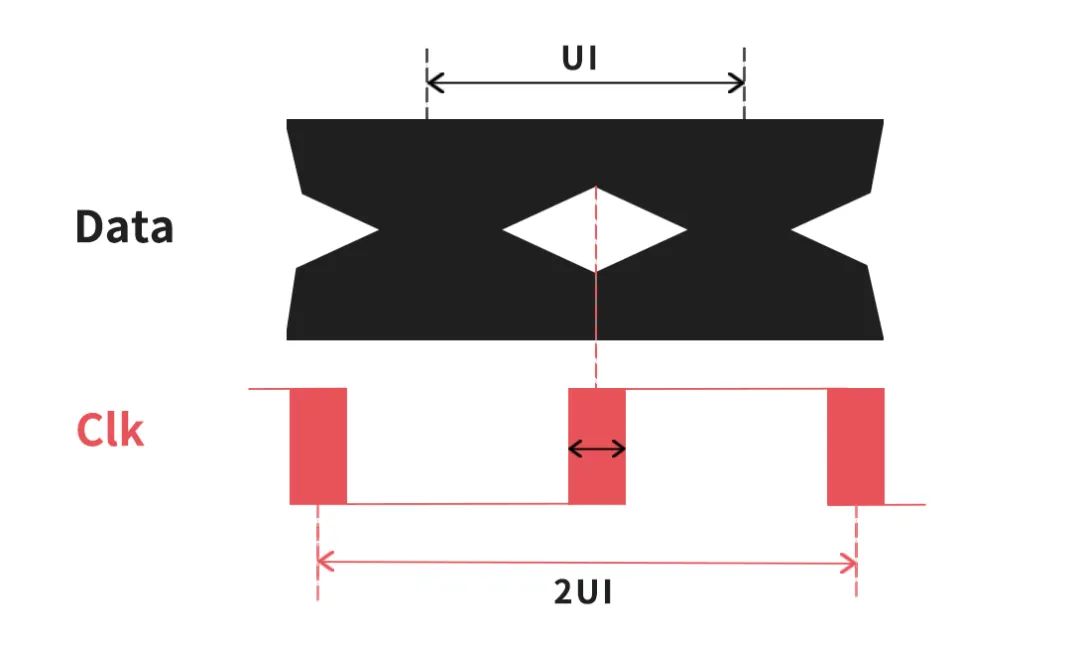
图2 时钟 Clk 半速率采样非理想的数据
相位噪声和抖动是量化同一现象的不同方式:信号时序误差。在时域,普通抖动测量有周期抖动、周期到周期抖动和累积抖动。在这些类型的抖动中,周期抖动 (如图1) 通常在数据表中给出。在频域中,振荡器的质量是由相位噪声测量来表征的,相位噪声测量检查的频谱时钟信号中的边带噪声频率。为了简单起见,假设理想时钟是带 a 的完美正弦波频率 FC,这样一个纯时钟的所有功率将集中在 FC (如图2)。相位噪声的影响是扩散功率进入边带,引起频率的轻微变化,而不是振荡器总是产生一个纯时钟信号,有时快一点:FC + ∆f,有时慢一点:FC - ∆f,时钟速度转化为时域的抖动,如下图 (图3、图4) 所示。总而言之,电力系统中的各种随机和确定性噪声源会引起抖动。
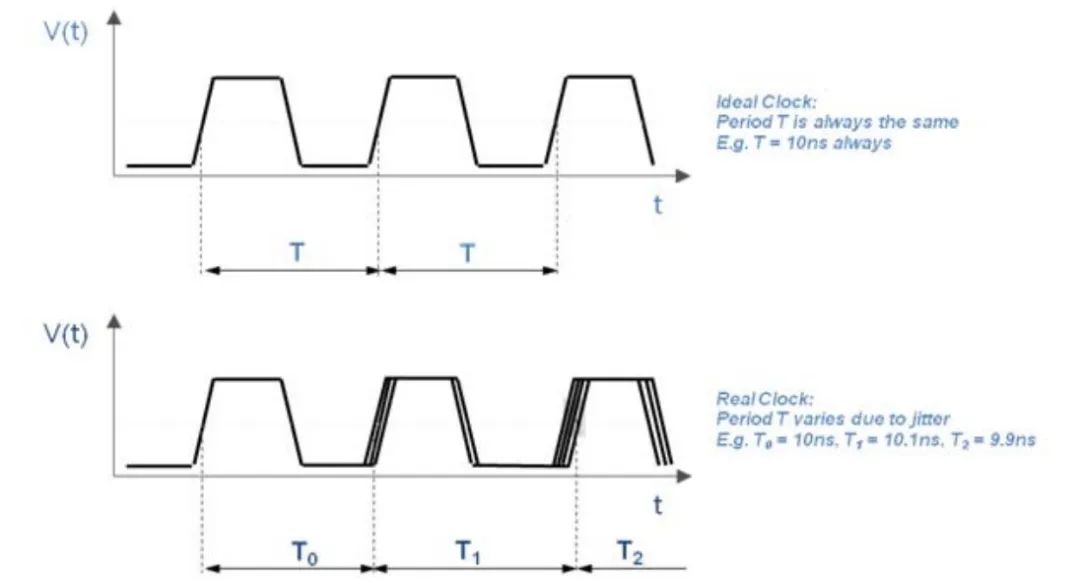
图3 抖动在时钟域的体现以及周期相位的变化
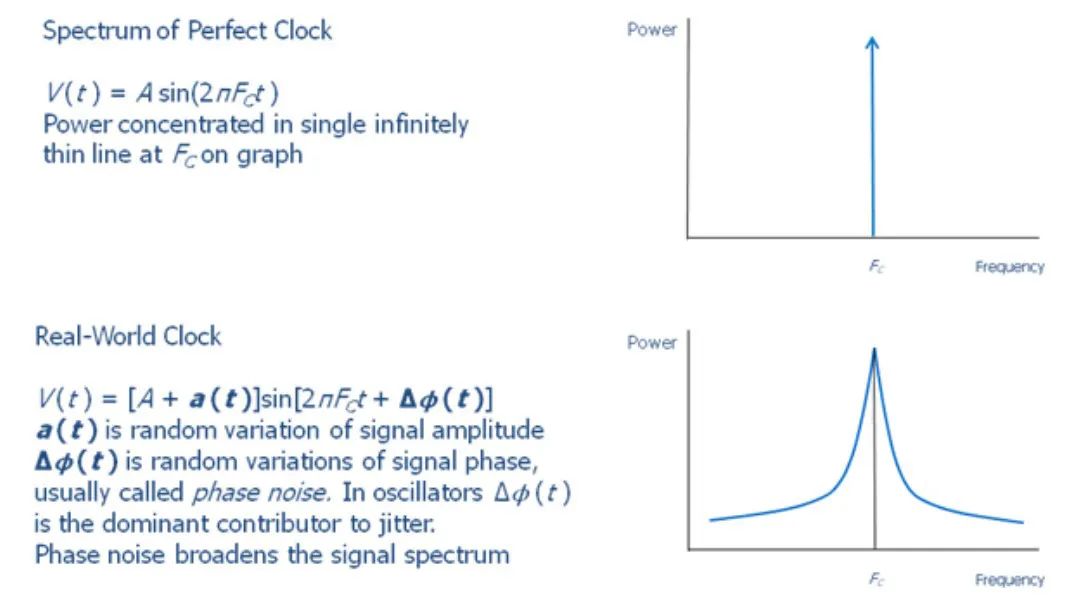
图4 抖动在频域的体现:能量积分
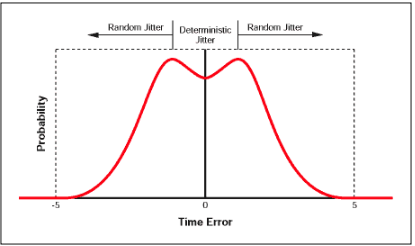
量化时域抖动 总抖动 (TJ) 等于确定性抖动 (DJ) 和随机抖动 (RJ) 之和。确定性抖动的常见来源是串音和同步输出切换。DJ 的峰对峰值是有限的,可以通过精心设计最小化,例如良好的 PCB 布线。DJ 的作用是为 RJ 的值增加一个偏移量。随机抖动 (通常是由于热噪声和其他不相关的噪声源) 是不可预测的,通常跟随一个高斯分布或正态分布,如下图 (图5) 所示:
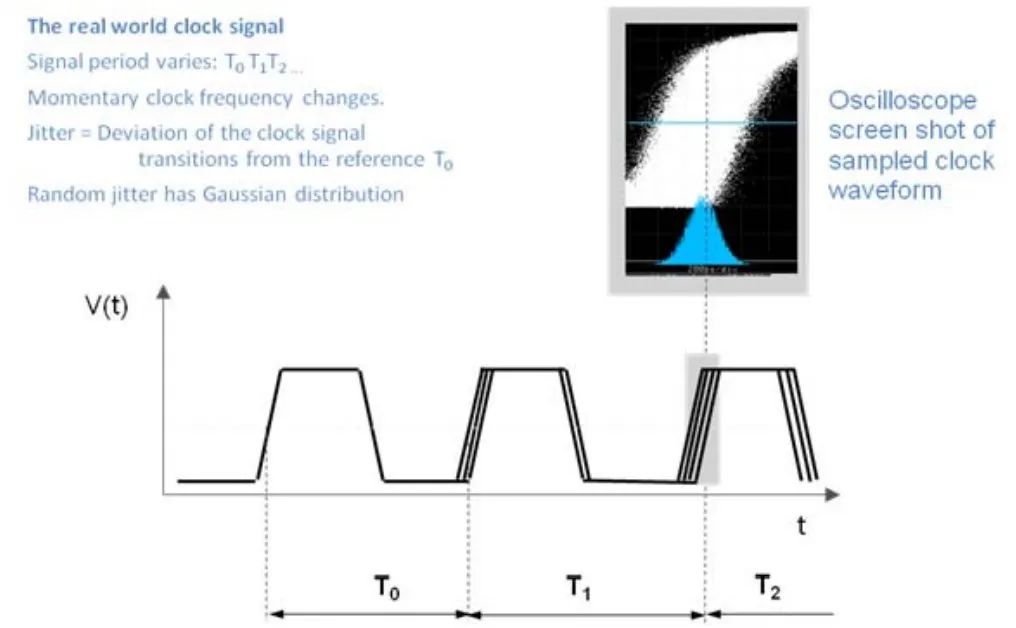
图5 随机抖动
随机抖动高度依赖于过程。下图 (图6) 表示了随机抖动峰间值与样品值的关系,与 DJ 不同,RJ 的峰间值为无限的;样品越多,RJ pk-pk 变化越大。
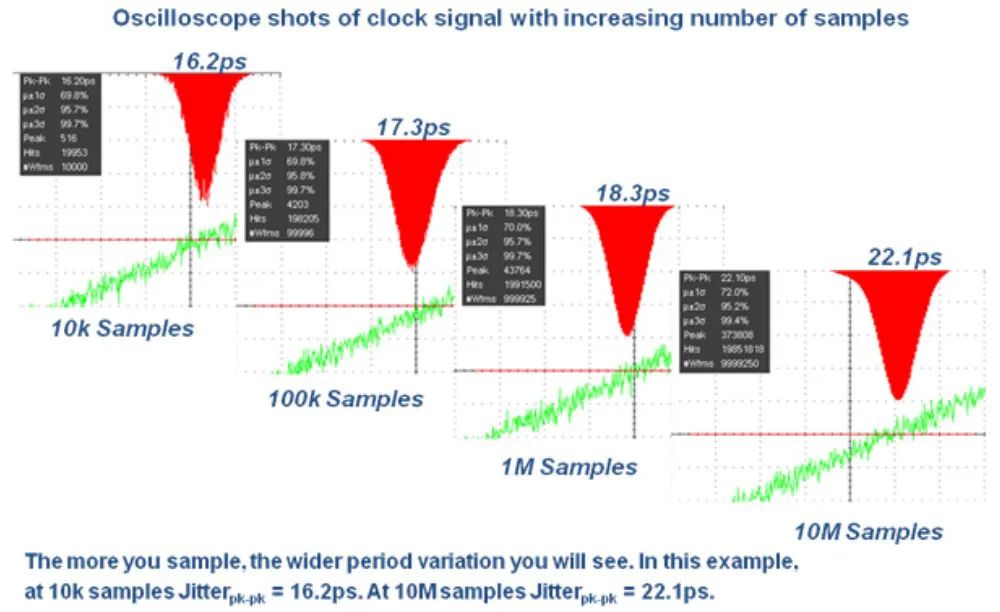
图6 随机抖动峰间值与样品值的关系
量化随机抖动的方法:均方根和峰对峰
周期抖动是时钟周期相对于平均时钟周期的短期变化。如果平均或参考周期为 To,则取周期抖动的采样为 T1-To,T2-To,T3-To... 以此类推,直到 10000 个样品 (JEDEC 标准 JESD65B)。将这些抖动样本绘制成直方图很可能会得到正态分布,如下图 (图7) 所示。理想情况下,抖动的平均值 µ 为零。µ 左边的值表示小于参考周期的时钟周期,和右侧的值大于参考时钟周期。µ (深蓝色) 的每边标准差为 1σ,约占抖动样本的 68%。而 µ (medium) ± 2σ ± 3σ (浅、中、深蓝) 约占 95%,±3σ (浅、中、深蓝) 约占 99.7%。
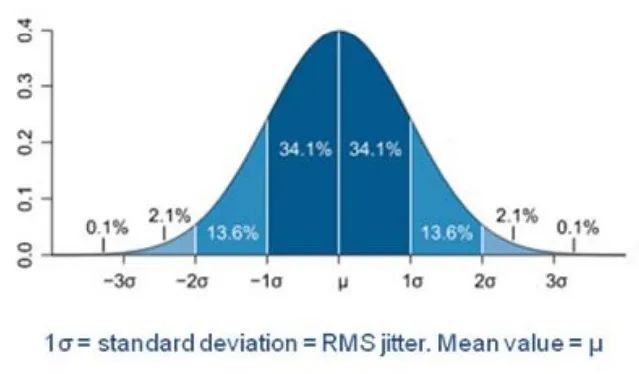
图7 周期抖动样本
正态分布产生两种常见的抖动规格
均方根抖动 (RJRMS) 或一个标准差的值 σ。因为这个值几乎不随数字变化对于样本的增加,它被认为是一个更有意义的测量。然而它只在纯高斯下有效分布 (没有确定性抖动)。
峰对峰抖动或正常曲线上从最小到最大测量的距离。在大多数电路中值随着采样次数的增而增加 (如图6)。为了得到一个有意义的峰对峰抖动值误码率 (BER) 也需要指定。
RMS抖动与峰间抖动和误码率的关系
在上图 (图7) 中,我们可以看到,在 6σ (平均值 ±3σ) 或 6xRJRMS 的峰对峰范围内,大约有 99.7% 的抖动样本都是有原因的。要解释 100% 的抖动样本是不可能的 — 高斯分布的故事延伸到无穷大。是什么决定峰对峰抖动是 6×RJRMS,7×RJRMS,还是 12×RJRMS?实现这一目标的有效方法是基于系统所需的误码率 (BER)。假设任何样本落在峰对峰范围之外会导致比特误差。因此如果要求 BER 目标为 10-12,则有必要进行选择除了 0.0000000001% 的时间外,该范围将包含所有时间的抖动。要使用此方法将 RMS 抖动转换为峰对峰抖动,只需将 RMS 乘以对应下图 (图8) 中 N 值适当的误码率:
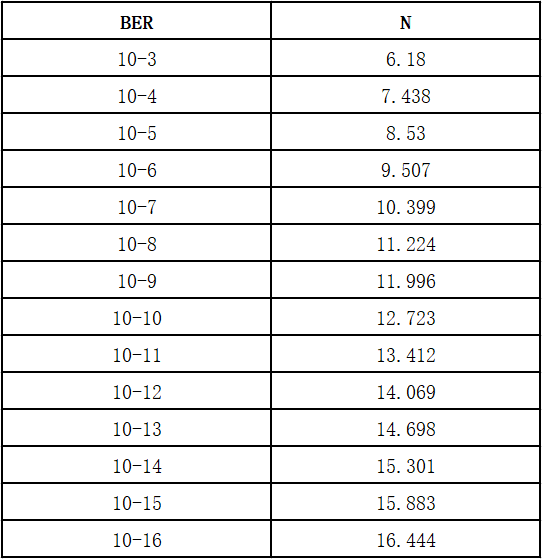
图8 误码率和均方根乘法器 N
例如 RJRMS=4ps,系统误码率要求为 1×10-12,对应的峰间抖动四舍五入为:RJ pk-pk=4x14.069=56.4ps。这个数字给了我们一个允许抖动预算的概念。粗略地说,如果 a 中的各种随机抖动源,通信链路加起来不超过 56.4ps,那么误码应小于 1×10-12。
预测与测量的峰对峰抖动
峰对峰抖动通常用两种方式描述:它可以按照前面使用 RMS 乘数的方式计算,这是基于一个定义的峰间抖动的预测误码率 (通常为 1×10-12)。或者可以使用测试设备进行测量。在这种情况下,采样的最小周期从最大周期中减去测量。正如我们之前所看到的,这取决于采样的数量。
预测值和实测值将不相同。测量值会给人一种系统抖动的感觉,但是相对于 BER 有些无意义。例如从 10,000 个样本中测量的峰对峰抖动不会告诉 BER 所需的峰间抖动 =1x1012,至少需要 1,000,000,000,000 个样本来完成此操作。因此 RJ pk-pk 通常根据定义的误码率从 RJRMS 计算。
量化频域抖动:相位噪声
正如前文中提到的,相位噪声描述了频域的抖动。接下来我们将从相位中看到在噪声信息中,提取 RMS 相位抖动值,该值通常在数据手册中给出,作为质量和性能的度量光谱纯度。下图 (图9) 中的频谱图是一个标称频率为 FC (也称为载波频率) 的真实正弦时钟,加上边带偏移噪声频率 FO。这意味着有时时钟会有稍微大一点的频率 FC+FO 和有时它会有一个稍低的频率 FC-FO。频率的微小变化表现为时钟的相移波形,因此称为相位噪声。
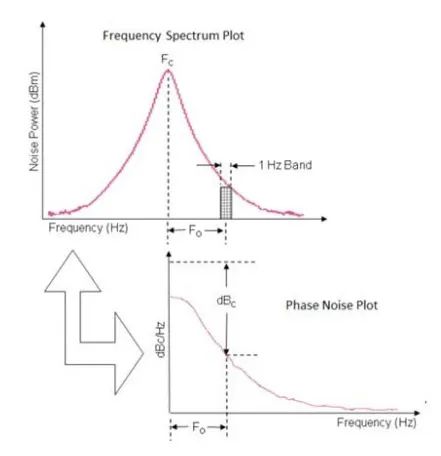
图9 频谱图
与载波频率 FC 的功率相比,在偏移频率 FO 的 1Hz 频带中的噪声功率称为 dBc,相位噪声的实际单位是 dBc/Hz,因为功率归一化到 1Hz 带宽 (相位噪声:dBc=相对于载波的 dB 功率)。

频谱和相位噪声图的区别
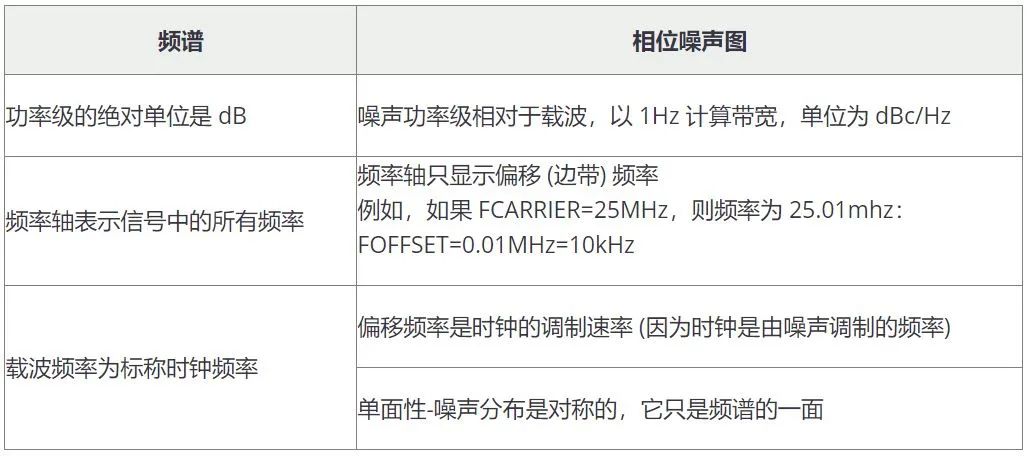
RMS Phase Jitter
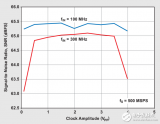
下图 (图10) 为 311MHz 振荡器的相位噪声图,在观察振荡器相位噪声图时,需要注意某些边带频率范围。
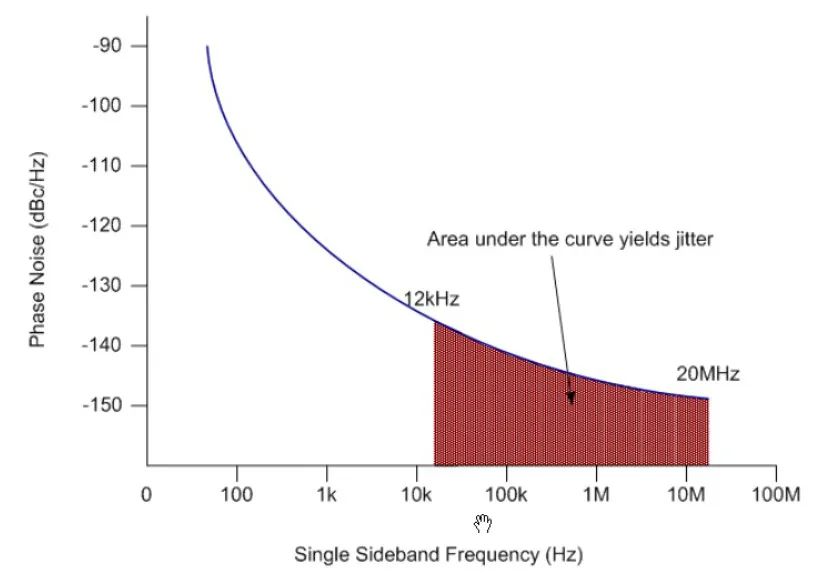
图10 311MHz 振荡器的相位噪声图
在电信行业,噪音 12kHz 至 20MHz 范围内的功率对定时性能非常重要,具体可参照上图 (图8):Noise Power (dBc) = Area under curve from 12kHz to 20MHz = -63dBc。由噪声功率 N 可以计算出以弧度为单位的 RMS 相位抖动值,公式如下:
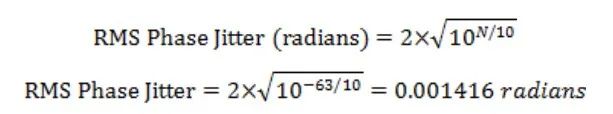
以弧度为单位的抖动值可以转换为以秒为时间单位的 RMS 抖动:
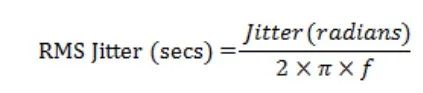
在此例中,振荡器频率 f=311MHz,所以可以得到:
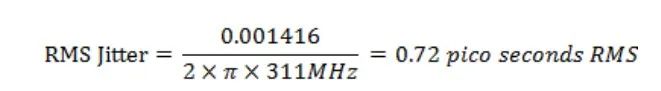
当抖动来自相位噪声图时,计算抖动的边带频率间隔必须始终为指定。
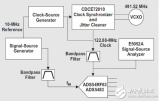
以下为大家进行举例说明:根据下图 (图11) 的 FPGA 规格参数要求,StratixV 的时钟输出来为 Broadcom 时钟,Phy 时钟要求输入指定为 1.5ps RMS 最大值。
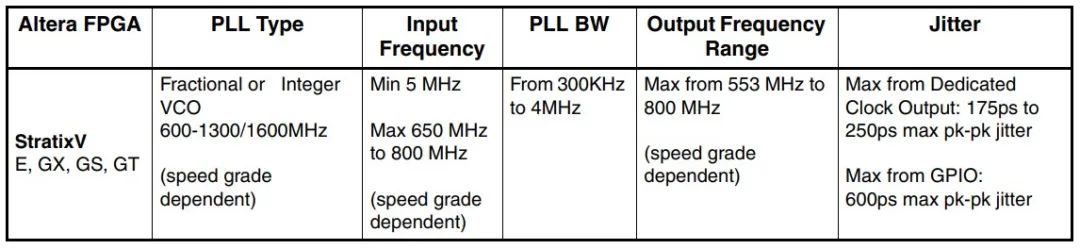
图11 FPGA 规格参数要求
1GE (千兆以太网) 的误码率要求为 1×10-12。根据上图 (图8),pk-pk 抖动大约等于 14 倍 RMS 抖动,因此可得出:
StratixV jitter (min) = 175/14 = 12.5ps RMS
StratixV jitter (max) = 250/14 = 17.9ps RMS
总结
本文为大家介绍了抖动的类型和概念,分别说明了量化时域抖动、随机抖动和频域抖动的方法。
-
抖动
+关注
关注
1文章
69浏览量
18853 -
相位噪声
+关注
关注
2文章
180浏览量
22838 -
频域
+关注
关注
1文章
87浏览量
26274 -
随机变量
+关注
关注
0文章
11浏览量
6453
原文标题:深入理解时钟抖动 Jitter
文章出处:【微信号:骏龙电子,微信公众号:骏龙电子】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
时钟抖动的基础
信号抖动的分类与测量
相位抖动是从哪来的?通信中有哪些抖动?




 抖动的概念和类型 量化时域抖动、随机抖动和频域抖动的方法
抖动的概念和类型 量化时域抖动、随机抖动和频域抖动的方法
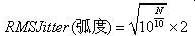












评论