无人机双余度电动舵机角度传感器故障检测的方法详解

引言

随着无人机技术的发展，无人机的应用范围越来越广，续航时间和任务半径越来越大，并且在执行任务的过程中携带的任务载荷和侦察打击设备越来越多，因此保证无人机在飞行过程中的安全性和可靠性就显得特别重要。

舵控系统作为无人机飞行控制系统的执行机构，其可靠性和安全性直接关系到无人机的飞行安全［1］。早在20世纪50年代初期，人们就认识到系统的单一通道设计不能保证系统功能的可靠实现，采用多通道设计能够大幅度提高系统的可靠性。由此产生了系统的余度设计技术，并迅速被飞机操纵系统等采用。余度技术是提高系统可靠性与安全性的一种有效手段，可以在降低元器件要求的同时有效地提高系统可靠性［2］。双余度舵控系统的基本思想是通过不同余度之间的切换来保证舵控系统的可靠性，因此在这个过程中就涉及到舵控系统的故障检测技术。

在舵控系统中角度传感器的作用是产生一个与舵面角度等效的电信号，将测量到的信号作为反馈引入到控制系统中，从而形成对舵控系统的闭环控制。所以角度传感器在整个舵控系统中具有重要的作用。为了防止舵机角度传感器故障造成舵控系统无法正常工作，在进行双余度舵控系统设计时，选用了共轴双余度电位器作为角度传感器。在舵机工作过程中及时准确地检测出单个角度传感器的故障并切换到另一余度，是提高舵控系统可靠性的关键。

目前舵机故障检测常用的方法是根据电机和传动机构的参数建立舵机的动力学模型，通过对比舵机的实际输出与参考模型输出之间的误差来检测舵回路是否发生故障［3-6］。针对双余度舵控系统工作过程中角度传感器的故障检测技术，本文提出了基于辨识参考模型的角度传感器故障检测方法。首先通过系统辨识的方法辨识出系统输出的参考模型，然后比较模型输出和实际角度传感器输出的残差变化是否超过阈值来判断电位器是否发生故障。

1 双余度电动舵机整体方案

无人机舵控系统可以分为电控部分和机械部分，机械部分通常情况下不会发生突发性故障，而是随着工作时间的增加逐渐出现性能下降、疲劳断裂等故障；电控部分由控制电路、无刷直流电机和角度传感器3部分组成，电机和角度传感器在运行过程中可能出现突发性故障，控制电路由于元器件的损坏或故障也可能出现突发性故障。结合舵控系统电控部分和机械部分的故障性质特点，设计了双余度舵控系统，整体方案如图1所示。

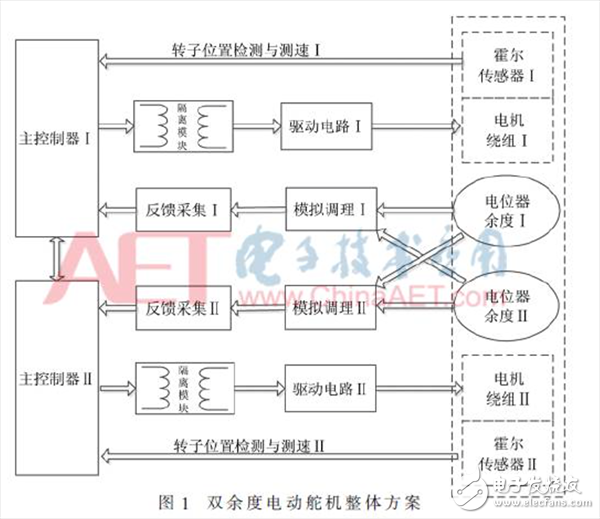
无刷直流电机、电位器和控制电路采用双余度设计，共用一套传动和减速机构。其中电机采用并联式双绕组无刷直流电机，每个绕组有一套独立的霍尔位置传感器，可保证电机独立工作。控制电路采用两套独立的控制系统，正常工作时，两套控制系统分别驱动双绕组无刷直流电机工作在热备份状态，当一个绕组出现故障时，从控制系统中切除，用另一个绕组工作［7］。

角度传感器采用共轴双联电位器，每联可以独立工作。每套控制电路分别采集角度传感器两个余度的信号，但是为了保证控制的一致性，在实际控制时两套控制电路以其中一路角度传感器信号作为反馈，当该路信号出现故障时切换到另一路角度传感器信号。正常工作时，两路角度传感器输出相同的反馈信息，当两路角度传感器输出信息不一致时，可以判断有一路电位器出现故障，但是无法判断哪路出现故障。因此要准确地判断角度传感器故障仅靠角度传感器自身是不够的，需要增加其他的判断依据。本文提出了基于辨识参考模型的无人机双余度电动舵机角度传感器故障检测方法。主要思想是通过两路角度传感器输出的差值判断角度传感器是否存在故障，然后通过参考模型确定哪一路出现故障，从而保证舵控系统可以得到准确的角度反馈信号。

2 参考模型建立

通过机理分析和理论推导的方式可以获得舵控系统的数学模型，模型参数可以通过测量或系统辨识的方法获取［8］。由于模型中有些参数很难准确地测量获得，因此本文首先采用机理分析的方法推导得到舵控系统的数学模型，然后通过系统辨识的方法确定模型的参数。

2.1 模型推导

舵机的结构简图如图2所示，主要由电机、减速机构和位置传感器组成。

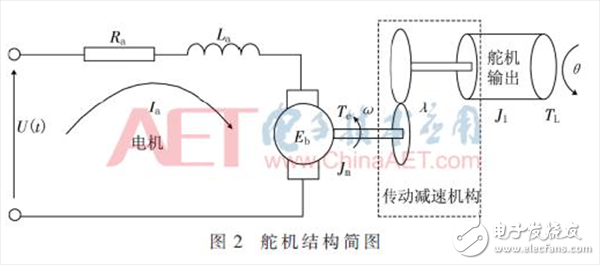
根据基尔霍夫定律可以得到电压平衡方程为：

由于此舵机中选用的无刷直流电机电感很小，接近于零，因此为了减小参数辨识的计算量和降低传递函数的复杂性，忽略电感的影响，将舵机的闭环传递函数等效为二阶系统。

2.2 模型参数辨识

本文研究的无人机舵控系统，以控制和反馈信号为模拟信号，范围为±10 V，对应±30°，频带范围为4 Hz。为了准确地辨识系统模型的参数，在选择输入激励信号时要求可以充分激发系统的动态特性。在系统辨识中白噪声是理想的输入信号，因此根据此舵控系统的带宽和输入输出工作范围，选择带宽为5 Hz、幅值为2 V的白噪声信号，利用Keysight 信号发生器的任意波功能产生。

由于舵控系统的输入输出信号均为模拟信号，因此利用泰克示波器的数据采集功能进行数据采集，采样周期为1 kHz。为了减小干扰和野值对辨识结果的影响，对采集的数据进行简单的滤波和剔除野值处理。

将处理好的数据导入MATLAB系统辨识工具箱，利用2.1推导的模型结构进行辨识参数，得到系统的输入输出模型为：

由于实际舵控系统的输入能量是有限的，因此舵回路内存在速率饱和的非线性特性，若直接对舵控系统的位置输入输出进行线性动力学建模，则当位置给定较大时，舵机在动态过程中的实际输出会因速率饱和而与系统模型输出具有较大的误差［9］。图3左边的曲线为输入角度较大时，由于速率饱和特性限制导致模型输出和舵机实际输出相差较大。

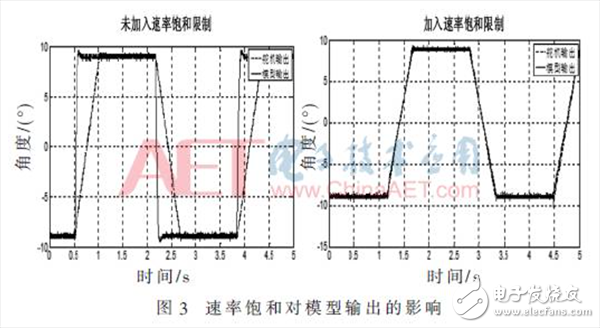
为了解决速率饱和特性导致实际输出和模型输出不一致的问题，在辨识出的舵控系统模型中加入速率饱和限制。速率饱和限制的表达式如下：

将位置限幅加入到辨识模型中，可以解决速率饱和特性造成的偏差。图3右侧为加入位置限幅后舵机实际输出和模型输出曲线，可以看出此种方法可以较好地解决由于速率饱和造成的偏差。

为了验证辨识模型在加载情况下的准确性，给舵控系统施加随机的弹性力矩，然后对比舵机实际输出和模型输出。试验结果如图4所示，给舵机施加±10 N·m的外部力矩干扰，辨识出的系统模型仍然可以较好地反映实际舵控系统的输出。因此辨识参考模型可以应用于双余度角度传感器的故障检测中。

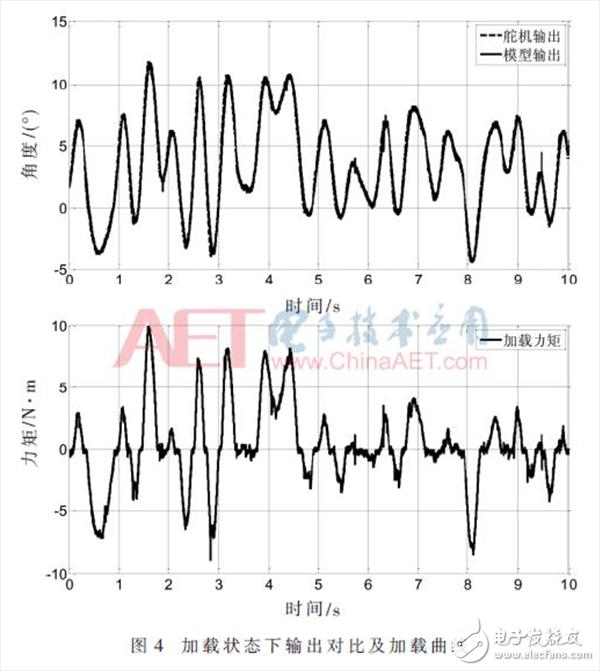
3 双余度角度传感器故障检测

角度传感器为双联共轴电位器，分别采用±15 V电压为电位器供电。由于双联电位器阻值分布和线性度不可能完全一致，导致舵机转动同一角度，电位器输出的电压变化也不完全一致。为了减小由于电位器差异造成的误差，利用角度传感器分别采集电位器输出电压和转动角度的对应关系，然后用最小二乘法拟合出电位器转动角度和输出电压值的线性关系。在实际工作过程中，将采集到的电位器电压值转化为角度，然后再进行控制。

3.1 故障检测方法

为了准确判断出电位器是否出现故障，并确定哪一个余度出现故障，采用的基本思想是：首先通过对比采集到两路角度传感器的角度值来判断角度传感器是否存在故障，然后将角度传感器的值和辨识参考模型对比确定出现故障的余度。具体检测步骤如下：

步骤1：分别采集两路角度传感器的电压值，并根据拟合公式将模拟电压信号转换成角度信号。

步骤2：计算两路角度传感器角度信号的差值，并判断差值是否超过故障的阈值。如果大于阀值则有一路信号存在故障，进入步骤3；如果小于阈值则两路角度传感器工作正常。

步骤3：计算两路角度传感器与辨识参考模型输出的差值是否超过阈值，如果超过则判断此路角度传感器信号出现故障。

步骤4：将舵机控制系统的角度传感器信号切换到没有故障的余度。

为了保证此故障检测方法的准确性，防止出现错检和漏检，上述故障检测步骤需要连续N个周期出现同样的问题时才判断电位器出现故障。

3.2 实验验证与结果分析

为了说明此种故障检测方法的有效性，选择典型的电位器故障，在不同的控制输入下进行实验验证。在舵控系统工作过程中，电位器滑动指针出现断损是最常见的故障。因此模拟处于工作状态的余度电位器出现断针故障，验证此故障检测方法能否检测出故障，并且切换到备份余度电位器来保证舵控系统的稳定运行。

为了模拟此种故障，在舵机工作过程中将主余度电位器的信号输出线切断。观察故障检测方法和故障切换的有效性。为了充分验证方法的有效性，分别选取具有代表性的正弦信号、阶跃信号和随机白噪声信号作为控制输入进行验证。

图5所示为控制信号是正弦信号时的故障检测结果。开始时余度1电位器反馈作为系统反馈信号接入到控制系统，在5 s左右将余度1电位器断路。从图中可以看出，在余度1反馈断路后，控制系统可以快速地将反馈信号切换到电位器余度2反馈，并且保证舵控系统工作的稳定可靠。

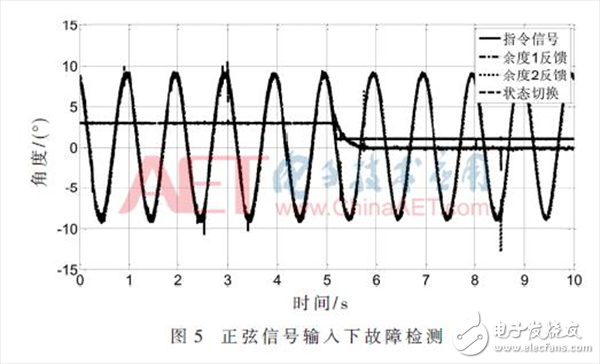
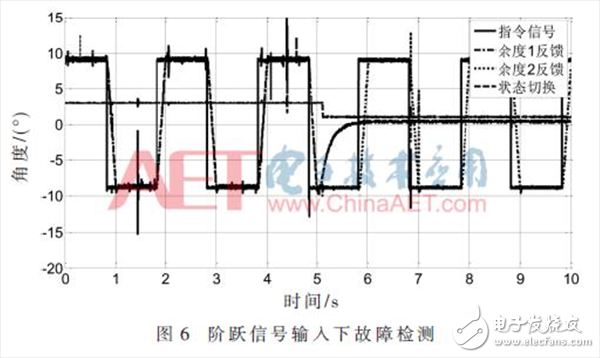
图6和图7分别为控制信号是阶跃信号和随机白噪声信号时的故障检测结果。开始时余度1电位器反馈作为系统反馈信号接入到控制系统，在5 s左右将余度1电位器断路。从图中可以看出，在余度1反馈断路后控制系统可以快速地将反馈信号切换到电位器余度2反馈，并且保证舵控系统工作的稳定可靠。

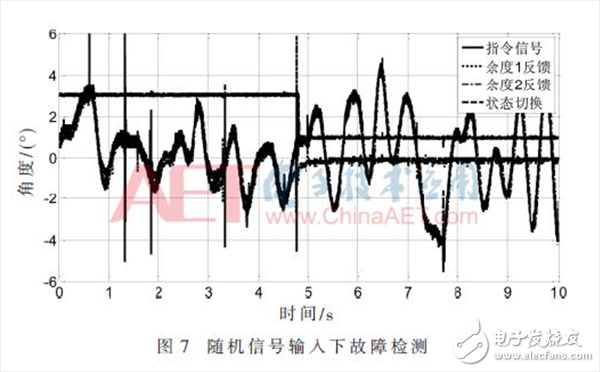
从测试结果可以看出，基于辨识参考模型的故障检测方法可以及时准确地检测出角度传感器的故障，并且切换到备份余度的角度传感器，保证舵控系统正常工作，提高系统的可靠性。

4 总结

本文研究了无人机双余度电动舵机角度传感器故障检测的方法。针对双余度角度传感器的特点提出了基于辨识参考模型的故障检测方法。首先通过理论推导和机理分析的方法建立了舵控系统的数学模型，然后利用模型辨识的方法确定了模型的参数。通过引入速率饱限制和位置限幅，解决了舵控系统模型由于速度饱和导致跟踪大角度输出时存在较大误差的问题，使模型即使在存在力矩干扰时仍然可以作为参考模型进行故障检测。最后给出了双余度电位器故障检测的步骤，并且通过实际的测试结果验证了所提出方法的有效性。