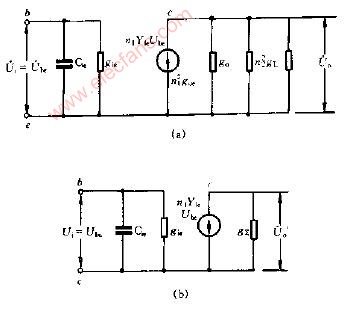
等效电路:

L:变压器漏感及元器件引线电感等杂散电感之和。
D、Cd:整流二极管,Cd为D的结电容。
Q、Coss:开关MOSFET,Coss为MOSFET的结电容。
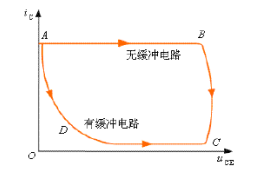
开关管由导通到截止时由于漏感L的存在,要通过R、C将其能量吸收掉,否则会产生一个尖峰电压影响到元件的可靠性以及造成EMI问题。
整流二极管截止时还有个反向恢复电流的问题,但是把反向恢复电流最大时当作分析的起使点,那在实际分析时过程还是一样的,只是初始状态不同。
考虑整流二极管这个回路,设流过L上的电流为I1(t):
流过结电容Cd的电流为

流过吸收电容C的电流为

根据Cd两端电压等于R、C两端电压得到微积分方程:

由于含有积分,方程求解不便,将其求导,得到3阶微分方程:

由于Cd很小,可以将其忽略以简化分析,得到简化后的微分方程:

考虑初始状态I1(0)=Io,I1’(0)=(Vin-Vo)/L,其中Io为开关管关闭时电流的最大值,应用拉普拉斯变换得到变换后的方程:

这是个2阶系统,应当让其工作在过阻尼状态防止振荡,因此要保证极点有2个相异实根,得到

应用拉普拉斯逆变换可以得到电流I1(t)的解:

电感L上的电压:

二极管D上的电压:

假定L=0.1uH,C=220pF,Vo=12V,Vin= -60V(此时MOSFET ON,变压器次级电压反向,Vin由12V跳变为-60V),R=2*sqrt(L/C)=42.6ohm。
DCM状态下Io=0,考虑不同的R值对波形的影响:


可以看到阻值越小,电压电流的波形振荡越多,峰值越高,越容易对回路产生不利影响,因此要保证工作在过阻尼状态,电阻R不能取小。
考虑R=47ohm时不同电容C对波形的影响:


可以看到电容C越大,电压电流变化率会减小,并且电压的过冲会减小,这样对EMI会有好处,但是峰值电流会变大。
考虑此时电阻R上的功率消耗,假定回路工作频率50KHz:

可以看到正常情况下吸收电阻消耗的功率与R值大小无关,只与C及C两端的电压有关,因此可以看到改善EMI是以增加消耗功率为代价的,会降低回路的总体效率,因此C也不能取太大,此时P=1/2*C*(Vin-Vo)^2*f 。
需要看到此时吸收回路吸收的不是漏感L上的能量,而是电压跳变在电容C上产生的能量。
考虑在CCM状态下,设Io=1A和2A
C=220pF时不同R值对波形的影响:




R=47ohm时不同C值对波形的影响:




可以看到当截止电流比较大时,电阻越大电流下降越慢,吸收电容上初始电压就会越高,对电容耐压要求就会越高,此时电感L及二极管D两端电压变化也会更快,对回路产生不利影响的可能性会更大,因此吸收电阻R取值也不能太大。
吸收电容上有初始电压是因为考虑二极管关断时两端电压不能突变,电感L电流也不能突变,从而电流经吸收电阻在吸收电容上产生了初始电压。
吸收电容的增大可以减小电压电流的变化率。
考虑此时吸收电阻R消耗的功率:

可以看到吸收功率始终随吸收电容C值的增大而增大,但是不同的截止电流随吸收电阻R值的变化会有不同的变化。
因此可以根据EMI的情况选取合适的C值,然后由此C值确定R值。
可以考虑一种确定R、C值的方法,在最大截止电流的情况下确定吸收电容C上的起始电压,这时可以计算出R值,这个R值是最大值,然后再由R值计算出C值,这时的C值是吸收电容的最小值。
考虑结二极管电容Cd的影响,设Cd=15pF:DCM状态:Io=0,



以上是不同的吸收电阻R,考虑不同的吸收电容C:



可以看到如果吸收电阻R偏大,流过结电容的电流也会增加,并且震荡也比较厉害,对二极管D会有不利影响,起不到保护二极管的作用。
吸收电容C的加大可以减小电压电流的变化率。
考虑CCM状态,Io分别为1A、2A:C=220pF,不同R的影响:






R=47ohm时不同C的影响:





可以看到截止电流越大,在二极管两端产生的尖峰电压越高,吸收电容越大,电压电流变化率越小,吸收电阻越大,电压尖峰越高。
以上的曲线是在初始状态I(0)=Io,I’(0)=(Vin-Vo)/L,I’’(0)= -Io/Cd/L的条件下求得的,不同得初始条件会得到不同得曲线。由于该初始条件并不一定正确,因此得到的曲线可能与实际观察到的波形会有较大差异,但是其变化趋势是可以参考的。
-
整流二极管
+关注
关注
5文章
351浏览量
31276 -
等效电路
+关注
关注
6文章
292浏览量
32774 -
开关管
+关注
关注
4文章
226浏览量
21658
原文标题:工程师不看后悔:开关管吸收回路计算分析
文章出处:【微信号:Mouser-Community,微信公众号:贸泽电子设计圈】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
开关电源电磁兼容及RC吸收回路设计
开关管吸收回路计算分析资料下载





 开关管吸收回路等效电路分析与设计
开关管吸收回路等效电路分析与设计















评论