怎样利用PWM实现DAC电路设计

周立功教授新书《面向AMetal框架与接口的编程（上）》，对AMetal框架进行了详细介绍，通过阅读这本书，你可以学到高度复用的软件设计原则和面向接口编程的开发思想，聚焦自己的“核心域”，改变自己的编程思维，实现企业和个人的共同进步。经周立功教授授权，即日起，致远电子公众号将对该书内容进行连载，愿共勉之。

本文为第三章：PWM 实现DAC 电路设计，内容包括：3.1 实现原理、3.2 电路设计、3.3 测试验证、3.4 参数总结。

本章导读：

当MCU 需要产生不同的模拟信号时，通常采用集成或独立的D/A 转换器实现。但是在要求低成本的场合，可以通过PWM 信号产生系统需要的直流和交流信号。

LPC824 内部有一个32 位PWM 定时器（SCTimer），它产生的PWM 信号搭配外围电路可实现高分辨率、低成本的DAC，比如，12 位DAC。

3.1 实现原理

>>> 3.1.1 PWM 信号时域分析

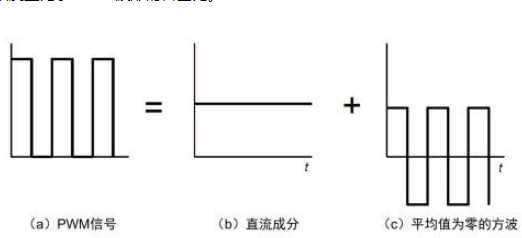
PWM（Pulse Width Modulation）是频率固定、占空比变化的数字信号，PWM 信号波形可以被分解为一个直流分量加上一个相同占空比，但平均幅度为零的新的方波，详见图3.1，由此可见，这个直流分量的幅度正比于PWM 波形的占空比。

图3.1 PWM 信号波形分解

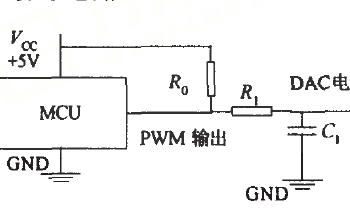
如果使PWM 信号的占空比随时间改变，那么其直流分量随之改变，信号滤除交流分量后将输出幅度变化的模拟信号。因此通过改变PWM 信号的占空比，可以产生不同的模拟信号。这种技术称之为PWM DAC，其原理可以形象地用图3.2 表现出来。

图3.2 使用滤波器电路获取PWM 的直流成分

>>> 3.1.2 PWM 信号频域分析

从频域分析进一步得到PWM 方式DAC的数学表达式。PWM 信号的函数波形详见图3.3，p 表示PWM 信号的占空比(0≤p≤1)，T表示载波周期。图 3.3 是在不影响分析结果的前提下，移动函数波形的时间原点，使波形符合数学中的常规脉冲函数波形，以简化数学分析。

图 3.3 PWM 信号函数波形

根据傅里叶理论，任意周期波形都可以分解为无限个频率为其整数倍的谐波之和，周期函数f(t)的傅里叶级数展开结果如下：

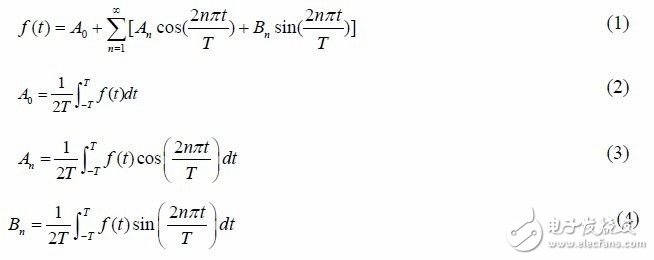
如果令K 表示PWM 信号f(t)的幅度，代入公式(2)~(4)，f(t)的展开系数分别如下：

从展开式系数可以看到，直流分量A0 项等于PWM 波形幅度乘以PWM 波形占空比，这是所期望的D/A 转换输出结果。通过选择合适的占空比，可以获得0~K 之间的任意D/A转换输出电压。

交流分量An 项是一系列频率为PWM 信号载波频率整数倍的高频正弦谐波，对于D/A转换转换是不需要的成分。举个例子，如果PWM 载波频率为1MHz，那么交流分量将是1MHz、2MHz、3MHz 等等。此时经过一个截止频率为1MHz 的理想低通滤波器，除去1MHz 及以上交流谐波，只剩下可任意设置直流分量，就是所期望的DAC 功能，DAC 表达式如下：

3.2 电路设计

PWM 实现DAC 的本质是需要保留直流分量去除交流分量，电路设计主要根据DAC 的分辨率，设计幅频曲线陡峭的低通滤波器，将交流成分衰减至可接受的范围内。对比无源RC、无源LC 低通滤波，由运放组成的有源低通滤波器，元件体积小，容易实现高阶滤波器，并且低输出阻抗，不存在带负载能力问题，电路框图详见图 3.4。

图 3.4 PWM 实现DAC 电路框图

该电路由两个三阶低通滤波器级联形成六阶低通滤波器，用于衰减LPC824 输出PWM信号的高频成分，实现12 位分辨率DAC。

>>> 3.2.1 DAC 分辨率

分辨率是DAC 的重要参数，存在两个误差源影响PWM 方式DAC 分辨率。首先，PWM信号的占空比只能表示有限的分辨率。在PWM 定时器最高时钟固定的情况下，DAC 分辨率由PWM 信号载波频率决定。例如，期望产生载波频率100kHz 的PWM 信号，PWM 定时器时钟为100MHz，这个时基在每个PWM 载波周期之中，最多提供1000 个计数值，通过指定PWM 定时器的比较值，最多提供1000 个PWM 占空比分辨率。

第二个误差源是PWM 信号中不期望的谐波分量所产生的峰峰值纹波详见图 3.5，纹波峰值至少需小于1/2 个LSB，这两个误差源加在一起决定总的DAC 分辨率不确定性。

图 3.5 影响PWM 方式DAC 分辨率的误差源

改善第一个误差源占空比分辨率，容易想到降低PWM 载波频率。在前面例子中，将载波频率由100kHz 降低至50kHz，对于100MHz 的时钟，PWM 占空比分辨率增加至2000 个。然而，更低的载波频率也降低了公式（6）中不期望谐波部分的基波频率，一次谐波现在变为50kHz 而不是100kHz，如果硬件有源低通滤波器维持不变，其截止频率不变，更多交流成分将穿过滤波器，谐波纹波峰值增加，会导致第二误差源增加。

由此可见，根据确定的硬件滤波器来选择PWM 载波频率，在两个误差源PWM 占空比分辨率和谐波纹波之间存在矛盾。先确定载波频率，再设计滤波器，是使得分辨率不确定性最小的方法。对于LPC824 的PWM 外设，设计12 位DAC 的计算步骤详细介绍如下。

设定PWM 定时器时钟。LPC824 运行时钟高达30MHz，这里我们留出一些裕量，选择10MHz 时钟，周期为100ns。

设定PWM 信号载波频率。考虑将信号的周期设置为可以被4096 整除，这样可以保证步进值为一个整数，保证转换的准确性与简便性。

因此PWM 的载波周期设定在409600ns，这样在每次DAC 的数字代码步进1 时，只需要将高电平持续时间加100ns，即步进一个计数值即可。我们可以轻松地算出PWM 的载波频率为2.44KHz。

计算硬件低通滤波器所需的衰减倍数，PWM 信号的交流分量中，基波频率最低，当占空比为50%时，基波的幅度最大，若这种情况下滤波器能将基波幅度衰减至1/2LSB 之下，则在所有占空比情况下，都可以将PWM 信号的交流分量衰减至1/2LSB 以下。因此可根据50%占空比时的基波幅度，计算所需的衰减倍数。

首先需要将n=1 代入公式（6），得到基波的幅度A_n=1：

然后，计算使得基波幅度小于1/2LSB 的衰减倍数A_filter。

总结实现12 位DAC 分辨率的计算过程，LPC824 的PWM 时钟设置为10MHz，载波频率设置为2.44kHz，硬件低通滤波器需将2.44KHz 频率分量衰减74dB 以上。

>>> 3.2.2 有源低通滤波器

在PWM 实现DAC 应用中，带宽、阻带滚降速率是两个重要的滤波器性质。滤波器带宽定义为幅频响应等于0.707 倍时的频率。滤波器带宽直接揭示了最大信号带宽，即PWM 方式DAC 能够有效处理的最大信号频率。阻带滚降速率是高频部分幅频响应曲线的斜率。带宽、滚降速率共同决定滤波器输出端看到的谐波纹波幅度。

通常低通滤波器为-20dB 每十倍频程每阶滤波器，若低通滤波器带宽设置为载波频率的1/10 频程，即0.244KHz，衰减-74dB 至少需4 阶低通滤波器。综合考虑带宽、滤波器电路的复杂程度，低通滤波器带宽设定在200Hz，使用两级3 阶巴特沃斯低通滤波器级联形成6阶滤波器，详见图 3.6。

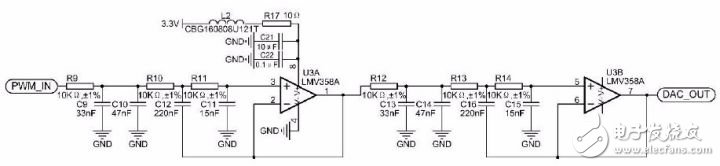
图 3.6 6 阶巴特沃斯有源低通滤波器电路

此滤波器电路的幅度曲线详见图 3.7，2.44kHz 频率成分衰减比例为100dB 左右，具有足够的裕量。如果只需用到10 位分辨率DAC，可只选择使用第一级滤波器。

图 3.7 6 阶有源低通滤波器幅频曲线

与LPC824 的ADC 信号输入滤波器类似，这里再次使用单运放的三阶滤波器电路拓扑，避免常规有源滤波器电路设计对运放的带宽要求。常规配置需要运放增益带宽积至少比输入信号的最高频率高5 到10 倍，否则当输入信号的频率成分高于增益带宽时，高频成分将直接馈通至输出。根据PWM 信号的最小占空比100ns，主要高频成分可达10MHz，需用到50M~100MHz 带宽的精密运放。这类宽带精密运放非常贵，有时相当于直接使用一个DAC芯片的成本。

而在图 3.6 中，使用3peak 公司增益带宽积仅为1MHz 的通用运放LMV358A 实现同样功能，使得滤波器的成本可接受。

3.3 测试验证

为验证所实现12 位PWM DAC 的有效性，特制作了实际的电路板进行测试，主要测试数据为DNL、INL、建立时间。

>>> 3.3.1 DNL

DNL 差分非线性定义为任意两个连续数字代码所输出步进电压的实测值与理想值之差。理想DAC 的步进电压为，每次严格步进一个LSB（DNL=0）。

在DAC 输入数字代码范围内，取若干点的DNL 测试验证（1LSB=3.3V/2¹²=0.81mV），数据详见表 3.1。可以看出，DNL 最大值为0.02 个LSB。

表 3.1 PWM DAC 的DNL 测试数据

>>> 3.3.2 INL

INL 积分非线性是表征DAC 精度的一个重要参数。在DAC 的全量程范围内，设置输入数字代码从小至到大，依次等间距输出一系列电压值，可以线性拟合出一条最贴近这些电压值的直线。理想情况下，DAC 是线性的，这些电压值应该全部落在该直线上。实际输出电压值与拟合直线的偏离程度，则表征了DAC 的非线性。

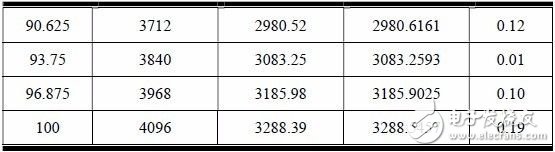
INL 测试数据详见表 3.2，从表中数据可以看出，INL 最大值为1 个LSB。

表 3.2 PWM DAC 的INL 测试数据

>>> 3.3.3 建立时间

建立时间是指从发出更新输出值的命令，到DAC 输出电压建立到最终值误差范围之内的时间间隔。建立时间受输出有源低通滤波器的带宽等参数影响，测试波形详见图 3.8。

图 3.8 PWM DAC 输出建立时间测试

从上图可以看出，建立时间ΔX 约为10ms。

3.4 参数总结

总结精度指标测试值详见表 3.3，用作对比的AD5623 是常见的独立12 位DAC 芯片。

表 3.3 PWM DAC 精度参数

表中数据表明，LPC824 的PWM 外设结合本电路所实现DAC 有非常好的差分非线性（DNL）、线性度（INL），与独立DAC 芯片基本一致。但建立时间慢，因此适合于输出低频、高精度的模拟信号。

---