神经网络的评估和内部状态解析

本文尽可能地减少使用数学公式，更多地基于可视化帮助读者入门，一方面降低了对背景知识的要求，一方面也是因为用这种方式介绍神经网络可能更易于理解。事实上，理解大部分机器学习的内容都只需要高中程度的数学知识，加上一点类比和抽象的能力。在此基础上入门机器学习是可能的，也是很多人所盼望的（否则很多人可能就放弃接触这个领域了）。

在本文中，我们将更仔细些地评估它的表现，同时查看它的内部状态，以得到一些关于它是如何运作的直觉。在本文的后半部分，我们将尝试在一个更复杂的数据集（狗、汽车和船舶）上训练神经网络，看看需要什么样的革新能将我们的网络提高一个等级。

可视化权重

让我们来训练一个分类MNIST手写数字的网络，和前一篇文章不同的是，我们直接映射输入层到输出层，不设置隐藏层。所以我们的网络看起来像这样。

用于MNIST的单层神经网络。10个输出神经元对应数字0-9

当我们向神经网络输入图像时，我们通过将像素“展开”为一列神经元来可视化网络，如下图左半部分所示。让我们集中注意力到第一个输出神经元的连接，我们将这个神经元标记为z，并将每个输入神经元和相应的权重标记为xi和wi。

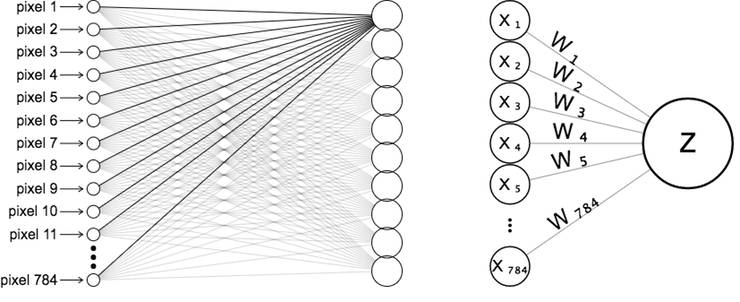
我们并不展开像素，而是将权重看成一个28x28的网格，其中权重的排列方式与对应的像素完全一致。上图右半部分和下图看起来不同，但是它们都表达了相同的等式，即z = b + ∑ wx。

另一种可视化每个输出神经元的像素权重乘积的方式

现在让我们看一下基于这个架构的训练好的网络，同时可视化第一个输出神经元接受的学习好的权重，这是负责归类数字0的神经元。我们给它们标上颜色，最低的权重是黑色的，最高的则是白色。

可视化MNIST分类器0-神经元的权重

眯起你的眼睛，右边那个图形看起来是不是有点像一个模糊的0？想一下这个神经元在做什么，这样可以更容易理解为什么这个图形是这个形状。这个神经元“负责”归类零，它的目标是输出一个较高的值（如果数字是零）或一个较低的值（如果数字不是零）。它将较高的权重赋值给一些像素，在表示零的图像中，这些像素通常趋向高值。通过这样的方法，对于表示零的图像，它可以得出较高的值。类似地，它将较低的权重赋值给一些像素，在表示非零的图像中，这些像素通常趋向高值，而在表示零的图像中，这些像素通常趋向低值。通过这样的方法，对于表示非零的图像，它可以得出较低的值。权重图像中相对黑的中心源自这样一个事实，表示零的图像的像素在这个位置通常趋向于最低值（数字零当中的空洞），而表示其他数字的图像的像素在这个位置通常有一个相对较高的值。

让我们来看看所有10个输出神经元学习到的权重。 正如我们所猜测的那样，它们都看起来像是10个数字有些模糊的版本，看起来好像是我们平均了许多属于每个数字类别的图像。

可视化MNIST分类器所有输出神经元的权重

假设输入是表示数字2的图像，我们可以预见负责归类2的神经元的值应该较高，因为它的权重是这样设定的：高权重倾向于赋值给在表示2的图像中趋向于高值的像素。其他神经元的一些权重也会与高值像素一致，使得他们的分数也有所提高。然而，共同之处要少很多，并且这些图像中的许多高值像素会被归类2的神经元中的低权重所抵消。激活函数不会改变这一点，因为它是单调的，也就是说，输入值越高，输出值越高。

我们可以将这些权重解释为输出分类的模板。这真是引人入胜，因为我们从来没有事先告诉过网络这些数字是什么或者这些数字是什么意思，然而它们最终却和这些分类的对象很相似。这暗示了神经网络内部机制的特殊性：它们形成了训练对象的表示，在简单的分类或预测之外，这些表示还有其他作用。当我们开始研究卷积神经网络时，我们将把这个表示能力提升至一个新等级，但就目前而言，让我们不要过于超前了。

相比提供的答案，这引发了更多问题。例如，添加隐藏层时权重会发生什么变化？正如我们很快会看到的，这个问题的答案基于我们在前一节中以直观的方式看到的东西。但在我们讨论这一点之前，让我们先检视一下我们神经网络的表现，特别是考虑它往往会造成哪些种类的错误。

0op5, 1 d14 17 2ga1n

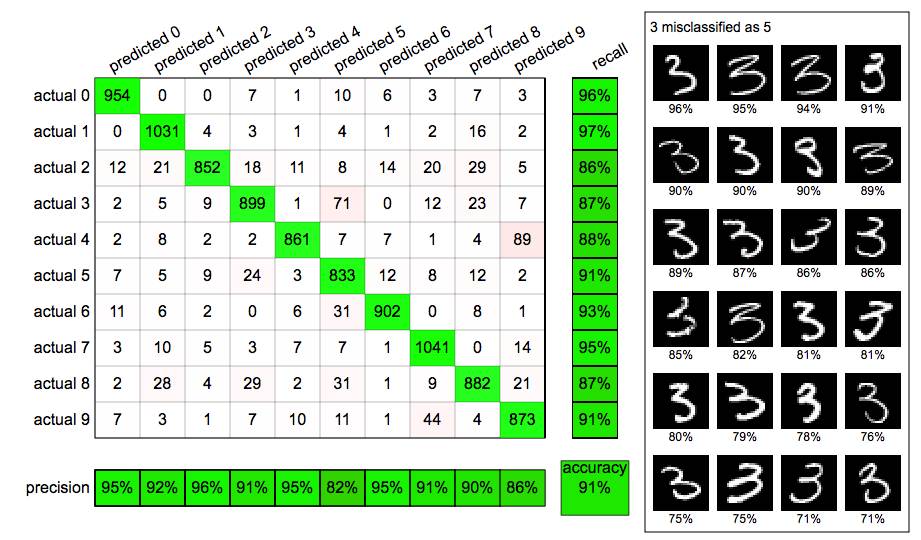
有时候，我们的网络会犯一些情有可原的错误。 在我看来，下面的第一个数字是9这一点并不是很明显。有人可能很容易把它误认为4，就像我们的网络做的那样。类似地，我们也可以理解为什么第二个数字3被网络误认为8。下面第三和第四个数字的错误更明显。几乎任何人都可以立刻认出它们分别是3和2，我们的机器却把第一个数字误认为5，对第二个数字是什么则毫无头绪。

我们的单层MNIST网络的一些错误。左边两个属于可以理解的错误，右边两个则是明显的错误

让我们仔细看看上一篇的最后一个神经网络的性能，它在MNIST数字上达到了90％的精确度。达到这个精确度的其中一个方法是查找一个混淆矩阵，这个矩阵将我们的预测分解成一张表格。在下面的混淆矩阵中，行对应MNIST数据集的实际标签，列对应预测的标签。例如，第4行（actual 3）、第6列（predicted 5）的单元格表示有71个3被我们的神经网络误标记为5。混淆矩阵的绿色对角线表示预测正确的数量，而其他所有单元格均表示错误的数量。

将每个单元格的顶部取样填入混淆矩阵，我们可以得到一些很好的洞见。

MNIST混淆矩阵中网络最自信的样本

这给了我们一个网络如何学习进行某种预测的印象。看前面两列，我们看到，我们的网络看起来在寻找大环形来预测0，寻找细线来预测1，如果其他数字碰巧具有这些特征，网络会误认。

玩坏我们的神经网络

到目前为止，我们只讨论了训练识别手写数字的神经网络。我们从中获得了许多洞见，但是我们选择的却是一个非常简单的数据集，这给了我们很多优势；我们只有10个分类，这些分类定义非常明确，其中的内部差异相对很小。在大多数现实世界的场景中，我们试图在非常不理想的情况下分类图像。 让我们来看看同一个神经网络在另一个数据集CIFAR-10上的表现。这个数据集包括6万张32x32的彩色图像，分属10类：飞机、汽车、鸟、猫、鹿、狗、青蛙、马、船和卡车。以下是CIFAR-10中的一些随机样本图像。

现在，很明显，我们必须面对这样一个困境，这些图像类别存在我们未曾应对过的差异。例如，猫可以面向不同的方向，具有不同的颜色和毛皮纹理，舒展或卷曲，还有许多其他我们在手写数字上不曾遇到过的变体。猫的照片也会与其他物体混杂在一起，加剧问题的复杂程度。

果然，如果我们在这些图像上训练一个双层神经网络，我们的精确度只有37％。这还是要比随机猜测好很多（精确度10％），但是远远低于我们的MNIST分类器达到的90％。使用卷积神经网络后，我们将大大提升精确度，不管是MNIST还是CIFAR-10。目前而言，我们可以通过审查权重来更准确地了解普通神经网络的缺陷。

让我们重复先前的试验，观察一个不带隐藏层的单层神经网络的权重，只不过这次我们将训练CIFAR-10中的图像。权重显示在下面。

可视化单层CIFAR-10分类器的权重

与MNIST的权重相比，明显的特征更少，清晰度也低很多。某些细节确实有直觉上的意义，例如飞机和船舶图像的外边缘大多是蓝色，反映了这些图像的周围倾向于是蓝天或者水体。由于特定类别的权重图像确实与属于该类别的图像的平均值相关，所以我们可以如先前一般期待斑点状的平均颜色凸现出来。然而，由于CIFAR类的内部一致性要低很多，我们看到的界限清晰的“模板”相比MNIST要不明显很多。

让我们来看看与这个CIFAR-10分类器相关的混淆矩阵。

毫无意外，表现非常差，精确度只有37％。显然，我们简单的单层神经网络不能应付这个复杂的数据集。我们可以引入一个隐藏层，多少改善一下表现。下一小节将分析这样做的效果。

添加隐藏层

到目前为止，我们专注于输入直接连接到输出的单层神经网络。隐藏层将如何影响我们的神经网络？在我们的MNIST网络中插入一个包含10个神经元的中间层看看。那么，现在我们的手写数字分类神经网络大概是这个样子：

MNIST双层神经网络

上面提到的单层网络的简单模板象征不再适用于这种情况，因为784个输入像素并没有直接连接到输出类。从某种意义上来说，我们过去“强制”我们原来的单层网络去学习这些模板，因为每个权重直接连接到一个类别标签，因而只影响该类别。但在我们现在引入的更复杂的网络中，隐藏层的权重影响输出层中所有10个神经元。那么我们应该期待这些权重看起来是什么样子呢？

为了理解发生了什么，我们将像原来那样可视化第一层中的权重，但是我们也会仔细查看他们的激活在第二层是如何合并的，从而得到类别分数。回顾一下前面提到的内容，如果图像在很大程度上和过滤器相交感，那么图像将在第一层的特定神经元中产生高激活。因此，隐藏层中的10个神经元反映了原始图像中这10个特征的存在性。在输出层中，对应于某个类别标签的单个神经元，是前10次隐藏激活的加权组合。下图展示了这一点。

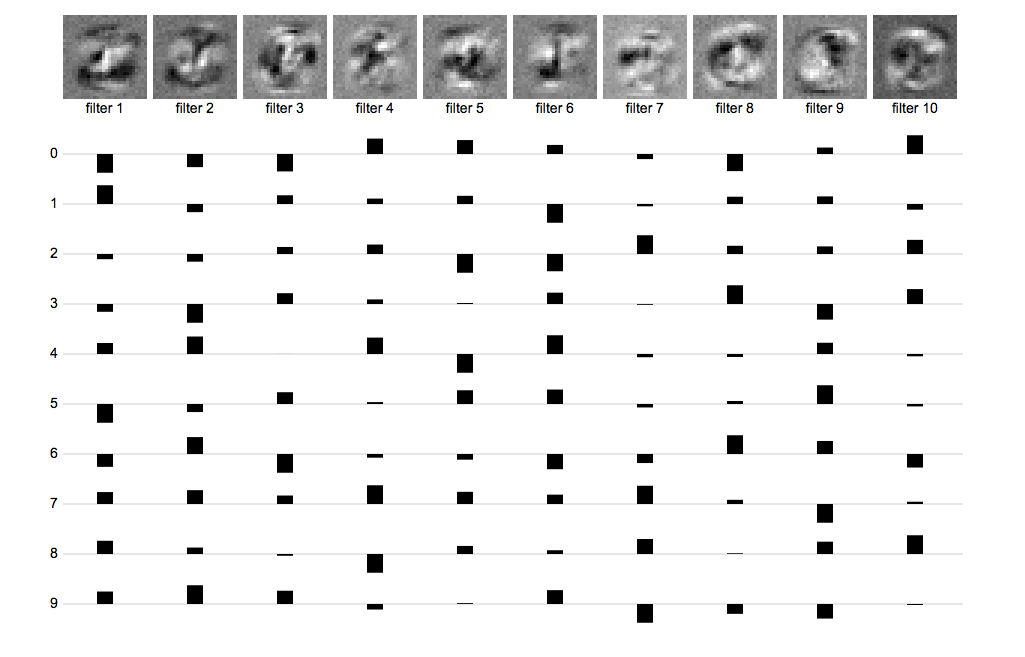
让我们先来看看上图顶部的第一层权重。它们看起来很陌生，不再像图像模板了。一些看起来像伪数字，其他看起来像数字的组成部分：半环、对角线、孔，等等。

过滤器图像下面的行对应于我们的输出神经元，每行代表一个图像类别。条形代表隐藏层传递给10个过滤器的激活对应的权重。例如，0类似乎偏爱外缘的值较高的第一层过滤器（因为数字零倾向于如此）。它厌恶中间的像素的值较低的过滤器（通常对应数字零中间的孔）。1类几乎与此正相反，钟爱在中间的值较高的过滤器，你可能已经想到了，那里对应数字1的竖笔。

这种方法的优势是灵活性。对于每个类别而言，更广泛的输入模式可以刺激相应的输出神经元。每个类别都可以由前一个隐藏层的若干抽象特征或者它们的组合来触发。从本质上讲，我们可以学习不同种类的数字零，不同种类的数字一等等。对大多数任务而言，这通常能改善网络的表现（尽管并不总是如此）。

特征和表示

让我们概括一下我们在本文学到的内容。在单层和多层神经网络中，每一层都有类似的功能；它将来自前一层的数据转换为该数据的“高层”表示。“高层”的意思是它包含了这些数据更紧凑、更突出的表示，就像内容概要是书的“高层”表示一样。例如，在上面提到的双层网络中，我们将“低层”像素映射到第一层网络中数字（笔划、圆圈等）的“高层”特征，然后将这些高层特征映射为下一层的更高层表示（实际数字）。这种将数据转换成更小但更有意义的信息的观念是机器学习的核心，也是神经网络的主要功能。

通过在神经网络中增加一个隐藏层，我们让它有机会在多个抽象层次上学习特征。这给了我们数据的丰富表示，其中，较前的层包含低层特征，较后的层包含由前层特征组合而成的高层特征。

正如我们所看到的，隐藏层可以提高精确性，不过程度有限。随着越来越多图层的迅速增加，很快精确性就不能再提升了，而且这会带来运算成本——我们不能简单地要求我们的神经网络在隐藏层中记忆图像类别的每个可能版本。事实证明，使用卷积神经网络是一个更好的方法。