正弦量的三要素是什么

正弦量是一个非常重要的概念，它描述了随时间变化的交流电信号。为了更好地理解和分析正弦量，我们需要掌握其基本要素等相关知识。下面将详细介绍这些内容。

一、正弦量的基本要素

正弦量具有三个基本要素，分别用于描述其大小、变化快慢和初始状态。

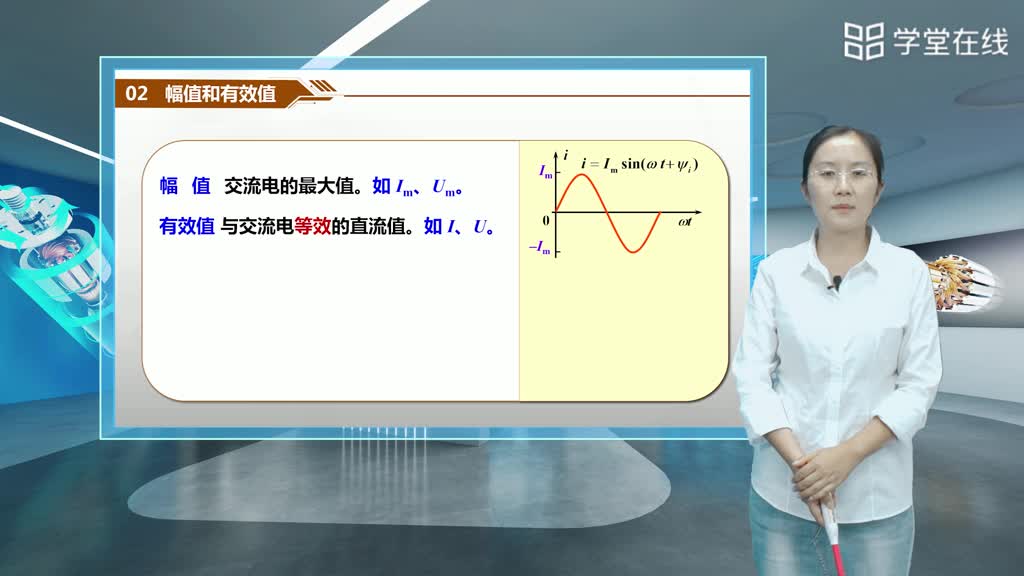
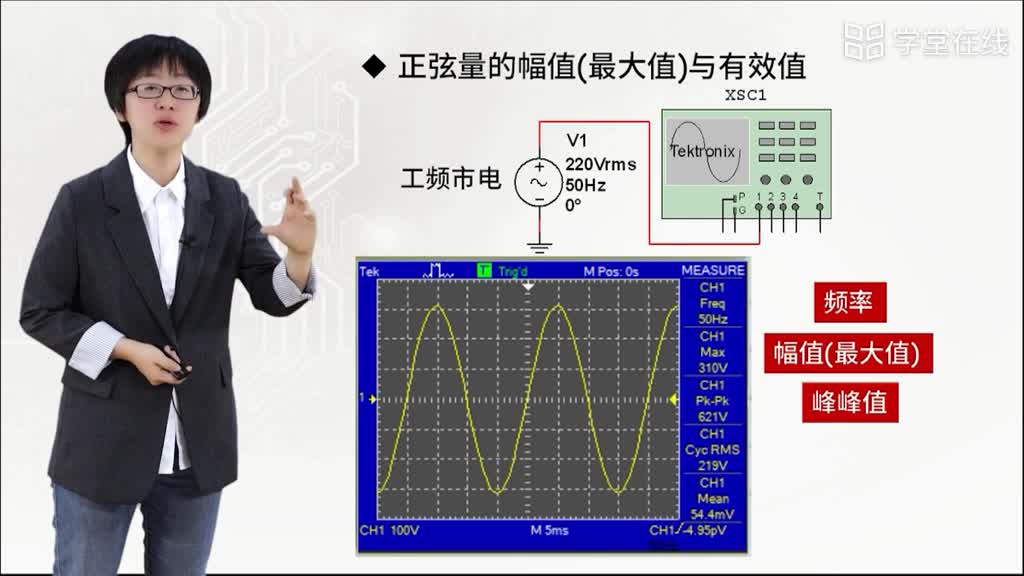
表示大小的量：有效值和最大值。有效值是指正弦量在一个周期内的均方根值，而最大值则是指正弦量在一个周期内所达到的最大值。这两个量共同决定了正弦量的大小。

表示变化快慢的量：周期T、频率f和角频率。周期T是指正弦量完成一个完整周期所需的时间；频率f是单位时间内正弦量重复的次数；角频率则是与正弦量的相位变化率相关的量。这三个量共同描述了正弦量的变化速度。

表示初始状态的量：相位、初相位和相位差。

二、复数的基本知识

复数是实数的扩展，可以用于表示有向线段。复数A的模r表示有向线段的长度，而辐角则表示有向线段与x轴正方向之间的夹角。复数有多种表示方式，包括代数式、三角式、指数式和极坐标式等。其中，代数式用于复数的加减法运算，指数式或极坐标式用于复数的乘除法运算。

三、正弦量的相量表示法

相量是一种用复数来表示正弦量的方法。相量的模表示正弦量的大小，而辐角则表示正弦量的初相位。为了与一般的复数相区别，相量的符号上通常会加一个小圆点。

最大值相量是用复数的模来表示正弦量的最大值。有效值相量则是用复数的模来表示正弦量的有效值。需要注意的是，由于正弦量有三个要素（大小、变化快慢和初始状态），而复数只有两个要素（模和辐角），因此在相量中只表示出了正弦量的大小和初相位，没有表示出交流电的周期或频率。这意味着相量并不等同于正弦量本身。

用相量表示正弦量后，我们可以将正弦量的加减、乘除、积分和微分运算都变换为复数的代数运算。这使得正弦量的计算变得更加简单和直观。此外，相量的加减法也可以用作图法实现，方法与复数运算的平行四边形法和三角形法相同。