如何使用EMI降噪

几乎所有的电子硬件工程师工作上都会面临不同程度的电磁波干扰(EMI)问题，尤其是最近几年电子产品逐渐朝高功率、高传输速率、小型化方向发展，使得EMI问题越来越复杂多样化，事实上这正意味着充分掌握EMI特性，同时在设计阶段事先导入预防措施采取正确的防范对策，才是有效克服日趋严格的EMI/EMC挑战最佳手段。本文将从基础物理的角度说明EMI信噪的定义与判别要素。

信号与噪讯

a.信号与噪讯的定义

所谓信号「Δ」是指相互隔离场所，利用光、电气等符号进行信息交流时的符号而言，此处所指的符号Δ是指表达语言、文字等信息时的记号体系。本实用EMI噪讯对策技术讲座所谓信号，则是指电气性的信号而言，通常电气性信号大多使用电压Δ或是电流Δ等符号。在模拟Δ信号有所谓的电压大小信号，它表示大小的信息，即使数字Δ信号也是直接使用模拟信号的电压，两者最大差异是数字信号利用大小，亦即0或是1的2值决定，而不是利用某个额定电压值决定信号的大小。

以上介绍的方式虽然是最基本的信号表示方法，不过也有其它表示方法经常被使用，例如在频率变调Δ领域，通常利用频率Δ表示信息。此外数字信号除了上述2值之外，偶而会使用3值以上的多值表示，由于2值信息比3值以上的信息处理上更容易，因此目前大部份的场合都使用2值方式。 如图1所示信号分为内载必要信息的信号(signal)与妨害该信号的噪讯(noise)两大类，广义上信号是必要信号与噪讯两者的组合，一般使用狭义定义，狭义上只将必要信号称为信号，原则上本讲座中的信号是指狭义的信号而言，使用特殊广义定或是要求明示时，利用一种被称为电气性信号作区隔。

图1 信号与噪讯的差异

b.信号歪斜与噪讯

刻意使信号歪斜使该结果成为期待的信号，此时刻意使信号歪斜的操作称为信号处理，非刻意的信号歪斜会妨害期待的信号，它相当于噪讯的定义，换言之它是信号本身歪斜造成噪讯发生。信号处理的用语通常使用数字信号或是模拟信号表示，在数字技术它被当作处理的意味，一般更广泛定义亦即在模拟信号中它包含处理的含意，因此使用信号处理的术语。

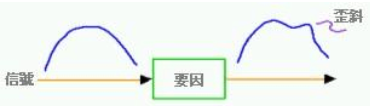
图2 信号的歪斜

c. S / N 比

信号与噪讯的大小一般以功率(power)「W 」表示，功率是指单位时间的能量Δ( J，焦尔)，亦即：

功率( W ) = 能量( J ) / 时间( s )

噪讯通常用信号对噪讯比S/N方式表示，而不是用绝对值表示，亦即：

至于功率比则以分贝(dB: decibel)表示，以对数表示功率比称为贝尔(B:Bel)，由于它所指的「比」原本是无次元数不过常被使用，因此特别添加单位名称Δ，成为贝尔(单位为1/10，数值变成10倍)。

分贝也使用在电压比，电压比的场合：

贝尔=20分贝

此处假设：

P : 电力 V : 电压 R : 阻抗 ( 电阻 )

消费功率与施加于阻抗的电压可用下式表示： P = V2 / R

由于贝尔的定义为电力比，因此电压比以贝尔表示时必需换算成功率比，此时2次方在对数变成2倍(此处请读者注意，贝尔为电力与电压时完全不同)。 电流比与电压比同样是: 贝尔 = 20分贝

如上所述S/N以功率比表示，不过信号通常利用电压表示它的大小或，是利用电压传输，因此以电压比或是电压评鉴，被视为适宜的情况相当多。

电路图中未标示的电路

使信号歪斜的要素

使信号歪斜的要素通常是某些电路组件，具体而言它是指为了刻意进行信号处理时，使用适合该处理作业需求的电路组件，例如电阻Δ、电容Δ等等，而这些电路组件一定被组装搭载在电路上，不过产生噪讯的电路组件一般都未装设在电路上，此处笔者想想要强调的是「即使电路图中未记载、标示，波形歪斜的要素仍旧存在」。电路图中记载的电路组件被视为理想性动作体，在电路图中电阻器属于纯粹理想性电阻器，电容器也是属于纯粹理想性电容器，然而实际使用的电子组件却偏离理想性具备现实特性。图3是组件的理想特性与现实特性，以频率特性Δ的形式进行比较。

图3 组件的理想特性与实际特性

由图3可知在频率较低的范围，组件几乎依照理想性动作，频率一旦变高组件的现实特性

从理想特性大幅偏离，因此选择电子组件时必需针对该组件实际使用信号频率范围，可以完全发挥理想性动作为前提选用，亦即可以使该组件在使用目的下的频率范围内以接近理想性动作。如图3所示频率较高处，电容几乎完全电感化(inductor)Δ，即使想用滤波器(filter)Δ消除噪讯，由于该现实特性限制，滤波器可能无法达成消除噪讯的预期目标。同样的信号线在电路图上拥有零阻抗(zero impedance)的理想特性，不过现实信号线则一定具备阻抗Δ(图4)。

图4 信号线具备阻抗

阻抗(impedance)内部若有电流流动就会产生电压(图5)，该电压就是一般所谓的「噪讯」。阻抗为电感(inductance)时阻抗值为 jωL，电流的频率( ω )一旦变高，对高频噪讯电流而言成为无法忽略电感造成的电压。此处请读者注意，笔直的一般信号线具备电感，电线呈环状卷绕时同样具备电感，尤其是刻意使电感变大的线圈(coil)Δ。类似这样即使电路图中未标示，实际存在的电路称为「电路图未标示的电路」，这点请读者务必牢记在心，因为「电路图未标示的电路」概念非常重要，它对日后处理EMI问题具有潜在性影响。

图5 电流在阻抗内流动时的特性

信号同样有各种形式，例如摩尔斯符号也是信号的一种。电气性信号分为交流与直流两种，直流Δ(考虑期间)属于一定的信号，相对的交流Δ则是随着电流流动方向变化的信号。虽然图7是电流的波形，不过电压的波形也相同。所谓交流是指平均值为0，正端(plus)与负端(minus)呈对称性波形而言。图7(b)是交流的代表正弦波形，正弦波形可用下式表示：

i = sin ( ω x t ) ω : 角速度

角速度对周期 具有以下关系: ω = 2π / T 频率 可用下式表示: 频率的单位是 Hz (Hertz)。

图7 电流的波形

正弦波形的交流为正弦波交流，最具代表性的交流单纯交流时，一般是指正弦波交流，不过交流却不限定是正弦波交流，根据以上述定义者全部都是交流，图8是常见的交流电波形。

图8 常见的交流电波形

正弦波形除了上述特性之外还需考虑它的位相Δ，一般信号并不是单纯的交流，它是变化复杂任意波形的信号(图9)。任意波形的信号可以用直流成份与多数(彼此频率相异)正弦波形相加方式表示(图10)。

图9 一般信号常见的波形

图10 任意波形的信号

表示某个信号包含哪些频率成份与百分比，称它是该信号的频率特性，信号包含的频率 ( f ) 有上限与下限的限制，信号包含的频率范围称为该信号的频域(频宽或是频幅)，虽然频宽也可以用绝对值 ( Δf ) 表示，不过一般都以信号频率的百分比 ( Δf / f ) 表示。此外，整合组件、组件的电路，决定输出、入之间哪些频率成份作何种变化等特性，称它为组件、电路的频率特性。频率特性具备两种含意，通常频率特性从横轴取频率的对数，纵轴为 刻度。图11是组件、电路的频率特性范例，该图是LC滤波器Δ的频率特性，由于LC滤波器的特性取决于QΔ定数值，因此该图可能显示LC滤波器的各种的特性。

图11 LC滤波器Δ的频率特性

电阻(符号为 R)属于可以限制电气流动的电子组件，严格来说它并不是单纯的阻抗体而是电气阻抗体。水等流体同样有阻抗称为流体阻抗，流体阻抗比电气阻抗复杂。此处假设电阻为

R，施加于电阻两端的电压为V，在电阻内部流动的电流为I，下列奥姆法则成立：

V = R x I

不论是交流或是直留奥姆法则都成立，两者主要差异交流的场合使用实效值，所谓实效值是指电力变成直流与等价的值而言。

图12 奥姆法则的特性

假设振幅 ( 最大值 ) 为 ，在正弦波实效值Vrms可用下式表示：

电容器属于具备储存电荷能力的电子组件，假设电荷量(电气量)为Q，电容器的容量( capacitance )(静电容量)为C，如此一来下式成立：

C = Q / V

电流是单位时间的电荷移动量，因此用时间将 CQ = V 微分变成下式(理想特性)微分方程式，接着解开该微分方程式变成下式：

式中的 为虚数( -1的平方根)Δ，数学上以 i 表示虚数，不过电气方面会与电流的 i 混淆因此使用 j，式中的 ω 表示信号的角速度。假设信号的频率为 f ，圆周率为 π ，如此一来角速度 ω 可用下式表示：

换言之角速度与频率呈比例，虽然角速度不是频率，不过与频率呈比例关系，因此经常被当作与频率相同意义使用，有时甚至将频率当作角速度单位表示，此时称它为角频率。此处假设：

如此一来：

它与上述奥姆法则相同的关系成立，式中的 Z 相当于阻抗 R 的定数，根据上式可知 Z 随着交流的频率改变，亦即它具备频率特性(电容的频率特性为Δ)， Z 又被称为电容的阻抗(impedance)，换言之阻抗Δ是将直流阻抗扩建成交流的概念。检测阻抗时如果检测对象包含电解质的话，此时若以直流检测由于电池作用会产生很大的误差，为防患未然通常都使用交流检测该阻抗。例如检测医学用白老鼠发情期的***阻抗检测器必需检测实质阻抗，因此以交流检方式测阻抗。此外，频率特性对交流有所谓的「flat」，阻抗不会随着频率变化。电感Δ(线圈，符号为 L)

(理想特性)的直流阻抗同样是0，不过对交流它反而会限制电气的流动。假设电感的阻抗为 L ，如此一来下式成立：

解开后变成：

式中的 ( j x ω x L ) 就是电感的阻抗，它的频率特性刚好与电容相反(电感的频率特性为Δ)，此外整合电阻、电容、电感的电路(例如滤波器)同样拥有阻抗，它的频率特性非常复杂。

电容器是利用电界、电感的磁界作用构成的组件，电容器以电界的形式储存能量(energy)，相形之下电感则以磁界的形式储存能量，不论是电容器或是电感都是储存能量的组件，相形之下电阻则是消费能量的组件。变压器是利用两组线圈的磁界相互结合体，将其中一方的电压传递至另一方，该相互结合以感应系数(inductance)表示，因此被称为相互感应电感。

图13 变压器的动作原理

连接负载阻抗的场合下式成立：

此外：

b.传输电气性信号

外来噪讯必定存在传递路径，该路径在电路图中未标示的情况非常多。接着要探讨图14两条相互平行信号线的特性。两条线相互独立时，理论上电气性信号的噪讯不会传递过来，不过两条信如果相互平行时，其间就会有浮游容量(stray capacitance)，噪讯会藉由浮游容量传递，电路图中未标示的电路亦即浮游容量几乎随处可见，因此又称为浮游容量Δ。 此外，相互平行两线之间还有相互电感，噪讯也会利用相互电感传递。相互直交信号线的电容与相互电感，若与相互平行信号线比较，相互直交信号线的电容与相互电感一般都可以忽略无视。信号在空中以电波(电磁波)形式传递，电波是整合电界与磁界的结果，天线除了将电波发射到空中称为放射，天线还可以攫取空中的电波。至于电气导体也具备天线效应，即使相隔一段距离相互成为天线，噪讯会透过放射传递。上述现象电路图中都没有标示或记载，不过噪讯会通过电路图中未记载的电路传递，它还包含伴随的信号，经过信号线传递的噪讯。