一、哈密顿图定义概念
哈密顿通路(回路)与哈密顿图(Hamilton图)通过图G的每个结点一次,且仅一次的通路(回路),就是哈密顿通路(回路)。存在哈密顿回路的图就是哈密顿图。
1.哈密顿通路
设G=《V,E》为一图(无向图或有向图).G中经过每个顶点一次且仅一次的通路称作哈密顿通路
2.哈密顿回路
G中经过每个顶点一次且仅一次的回路称作哈密顿回路
3.哈密顿图
若G中存在哈密顿回路,则称它是哈密顿图
4.定义详解:
(1)存在哈密顿通路(回路)的图一定是连通图;
(2)哈密顿通路是初级通路,哈密顿回路是初级回路;
(3)若G中存在哈密顿回路,则它一定存在哈密顿通路,反之不真
(4)只有哈密顿通路,无哈密顿回路的图不交哈密顿图;
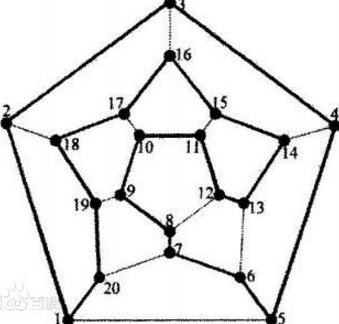
二、判断条件
与欧拉图的情形不同,到目前为止还未找到判断一个图是否是哈密顿图的非平凡的充要条件。事实上这是图论中尚未解决的主要问题之一。哈密顿图有很多充分条件,例如,
(1)若图的最小度不小于顶点数的一半,则图是哈密顿图;
(2)若图中每一对不相邻的顶点的度数之和不小于顶点数,则图是哈密顿图。
另外,还有很多用度序列、度和、图的坚韧度等参数给出的充分条件。
三、哈密顿图的充分条件和必要条件
定理1:设无向图G是哈密顿图,V1是V的任意的非空子集,则
p(G-V1)≤|V1|
其中,p(G-V1)为从G中删除V1(删除V1中各顶点及关联的边)后所得到的图的连通分支,|V1|为V1集合中包含的顶点个数。【哈密顿图存在的必要条件】
推论:有割点的图一定不是哈密顿图
设v是图中的割点,则p(G-v)》=2,由上述定理知G不是哈密顿图
(2)设G是n(n》=3)阶无向简单图,若对于G中的每一对不相邻的顶点u,v,均有
d(u)+d(v)》=n-1
则G中存在哈密顿通路。又若
d(u)+d(v)》=n
则G中存在哈密顿回路,即G为哈密顿图。【哈密顿图存在的充分条件】
其中d(u),d(v)分别代表顶点u,v的度数。
定理2:设G是n(n≥3)阶无向简单图,如果G中任何一对不相邻的顶点度数之和都大于等于n,则G是哈密顿图。
推论:设G是n(n≥3)阶无向简单图,如果G中任何一对不相邻的顶点的度数之和都大于等于n,则G是哈密顿图。
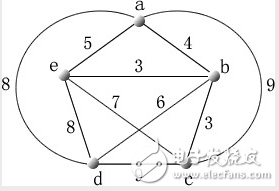
定理3:在n(n≥2)阶有向图D=中,如果所有有向边均用无向边代替,所得无向图中含生成子图Kn,则有向图中存在哈密顿图。
推论:n(n≥3)阶有向完全图为哈密顿图。
哈密顿路径也称作哈密顿链,指在一个图中沿边访问每个顶点恰好一次的路径。寻找这样的一个路径是一个典型的NP-完全(NP-complete)问题。后来人们也证明了,找一条哈密顿路的近似比为常数的近似算法也是NP完全的。
四、如何判断哈密顿图
1.常用方法判断是哈密顿图:
(1)若能通过观察找出图G中的一条哈密顿回路,则G当然是哈密顿图。
(2)若一个无向图G满足上述(2)中的条件,一个有向图D满足上述(3)的推论的条件,则G、D都是哈密顿图。
2.破坏哈密顿图存在的必要条件,判定不是哈密顿图:
设n阶图G是哈密顿图,则G应该满足以下诸条件:
(1)G必须是连通图;
(2)G中的边数m必须大于等于顶点数n;
(3)若G中存在2度顶点v,即d(v)=2,则与v关联的两条边ei,ej必须在G中的任何哈密顿回路上;
(4)若G中存在每条哈密顿回路中出现的边,不能构成边数小于n的初级回路(圈);
破坏以上诸条件中的一条,都不是哈密顿图。
-
哈密顿图
+关注
关注
0文章
3浏览量
1304
发布评论请先 登录
相关推荐

DNA编码的学习
电子关联对聚乙炔双激子态的影响
LaSrAlO4中Cu2+的自旋哈密顿参量的理论分析
ZigBee与哈密瓜不得不说的故事
哈密顿回路算法
永磁同步直线电机位置控制
模拟量子计算的未来前景将一片光明
模拟量子计算有着优异的表现,未来将具有广泛的应用前景
模拟量子计算的实力前景不可限量
基于量子软件的量子绝热近似算法求解
基于高光谱的不同成熟期哈密瓜坚实度研究





 如何判断哈密顿图_哈密顿图的必要条件
如何判断哈密顿图_哈密顿图的必要条件










评论