通过减少对低地球轨道卫星的依赖以提高GPS精度

作者梅根·O·摩尔 (MeganO. Moore)，弗吉尼亚理工学院暨州立大学

作为基础设施的重要组成部分，全球定位系统 (GPS) 提供定位、导航和定时 (PNT) 信息，这些信息对于应急响应、测量和建筑以及农业等众多行业至关重要。鉴于其广泛的使用和重要性，人们越来越担心该系统容易受到干扰、欺骗和其他威胁，美国运输部也因此出台立法，要求为 GPS 服务提供补充和备份。

在中地球轨道 (MEO) 部署卫星（无论是升级 GPS 还是建立新的卫星星座）的成本高昂，导致人们对使用现有机会信号的兴趣日益浓厚。这些信号不是为 PNT 设计的，但可以用于仅有多普勒定位的情况，这只需要有关卫星轨道和传输频率的公开信息。随着 Starlink 和 OneWeb 等大型低地球轨道 (LEO) 星座的发射，仅使用多普勒定位作为 GPS 备份的可行性增加了。不仅有更多可用的机会信号，而且这些信号的路径损耗更低，因为卫星距离地球更近，而且低地球轨道卫星的速度更快，从而导致多普勒频移更大、更容易测量。

低地球轨道星座在仅多普勒定位和导航方面的潜在用途是一个活跃的研究领域。近日，弗吉尼亚理工大学的研究员 Mark Psiaki 博士发表了一篇论文，表明当同一星座的八颗卫星同时出现时，可以达到与 GPS 相当的精度水平。然而，随着当前低地球轨道卫星的部署，需要八颗可见卫星，这限制了这种方法在实践中的实用性。我和弗吉尼亚理工大学国家安全研究所的 William “Chris” Headley 博士、Wireless@VT 的 Michael Buehrer 博士正在合作探索通过随时间对每颗卫星进行多次测量，以时间分集代替空间分集，以更少的卫星进行操作的可能性（图 1）。最近，我们证明了使用 MATLAB 和 Satellite Communications Toolbox 这种方法的可行性。我们不仅表明，几乎从地球上的任何地方都可以看到平均至少五颗卫星，而且四颗卫星实现的空间多样性与八颗卫星相当。

了解 GDOP 和 D-GDOP

为了分析 GPS 误差，研究人员开发了一种称为几何精度稀释 (GDOP) 的度量标准。GDOP 量化了卫星相对于接收器的几何排列，较低的 GDOP 值表示几何配置更好，因此定位精度更高。例如，如果将一颗 GPS 卫星放置在正上方，将另外三颗卫星放置在地平线上，则其 GDOP 测量值会相对较低，而如果将四颗卫星聚集在同一区域，则其 GDOP 测量值会较高，因此定位精度会较低。

一种称为 D-GDOP 的类似概念已经为多普勒定位而开发。与 GPS 使用的传统 GDOP 公式不同，D-GDOP 考虑了视野中卫星的速度和加速度。因此，最小化 GDOP 的卫星几何形状不一定会使 D-GDOP 最小化，反之亦然。更进一步来说，时间多样化的 D-GDOP，或者 D-GDOPT，是相同的概念，但应用于一种方法，其中对每个卫星的多普勒测量是随着时间的推移而不是一次性进行的。在我们的研究中，我们想看看 D-GDOPT 的衡量标准（例如，使用四颗卫星）与使用八颗卫星的 D-GDOP 测量值进行比较——这将使我们能够确定时间分集是否可以作为空间分集的充分替代品。然而，首先我们需要验证，对于给定的低地球轨道 (LEO) 星座而言，预期至少有四颗卫星进入视野是合理的。

分析卫星可用性

在评估卫星可见性时，首先要考虑的因素之一是卫星的地平线以上高度。以 GPS 为例，通常使用 10 度的遮盖高度 - 任何高于该高度的卫星都被视为可见，忽略障碍物造成的潜在阻挡。对于低地球轨道卫星的分析，我们需要应用类似的掩模，但要考虑到这些卫星用于通信的光束，这些光束比 GPS 卫星使用的光束要窄得多。根据技术文档和向联邦通信委员会 (FCC) 提交的文件，我们将 OneWeb 卫星的仰角设置为 25 度，将 Starlink 卫星的仰角设置为 40 度。在低于这些掩模的高度，来自卫星的信号可能太弱而无法可靠地使用。

接下来，我们需要确定从地球的各个位置可以看到哪些卫星。为了评估全球范围内的可用性，我们使用来自 Starlink 和 OneWeb 卫星的真实轨道数据，检查了全球每 10 度纬度和 60 度经度的可见性。具体来说，我们使用了从 CelesTrak 下载的这些星座的双线元素 (TLE) 数据。

利用 MATLAB 和Satellite Communications Toolbox，我们创建了一个卫星场景，以根据下载的数据对轨道卫星进行建模和可视化。我们使用 satelllite 函数读取和解析基于文本的 TLE 文件以获得完整的轨道——Starlink 大约需要 95 分钟，OneWeb 大约需要 110 分钟。我们几乎立即就能在卫星场景查看器中看到卫星轨道。这个 link 函数使我们能够执行链路分析，以确定在地面上，特定接收器可以使用每颗卫星信号的时间间隔。

然后，我们编写了一个 MATLAB 脚本，循环遍历所有纬度和经度组合（分别以 10 度和 60 度为增量），并计算每个位置视野范围内的平均卫星数量（图 2）。分析显示，在所有检查地点，平均可见至少五颗卫星，而在一些距离赤道较远的地区，可见卫星数量则更多。

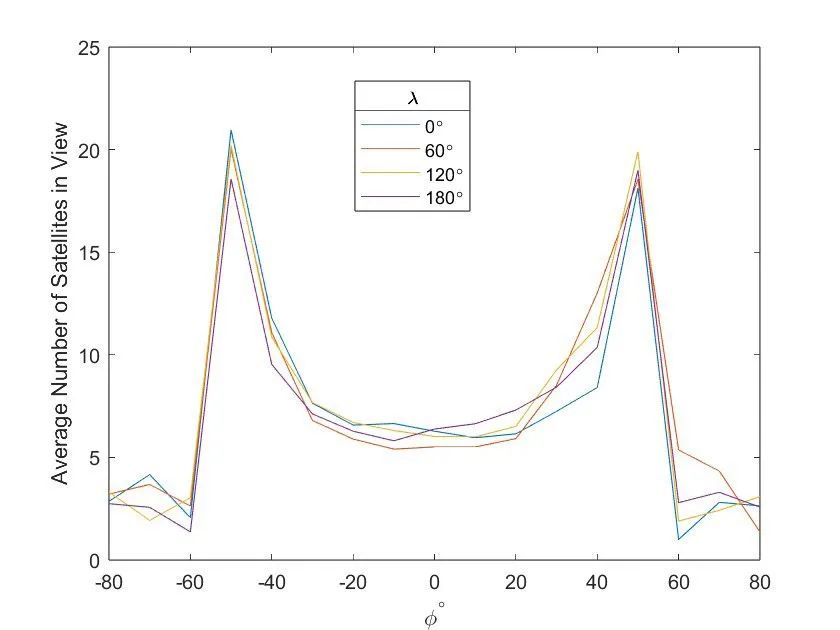
图 2. OneWeb 星座（上图）和Starlink 星座（下图）在不同纬度的卫星可见性。在赤道附近的纬度地区，可见的卫星通常较少，因为赤道上一度经度所覆盖的距离大约是纬度 60 度上一度经度所覆盖的距离的两倍。

评估时间多样化的 D-GDOP

一旦我们确定，平均而言，单个星座中的五颗或更多颗 LEO 卫星可能从任何位置都可见，下一步就是计算时间差异的 D-GDOP 指标，并将其与使用八颗卫星计算的传统 D-GDOP 指标进行比较。尽管理论上可以使用一颗卫星在八个不同时间进行多普勒测量，但实际上这会产生极高的 D-GDOPT 因为计算中使用的速度矢量缺乏多样性。根据我们对卫星可见性的分析，我们选择使用四颗卫星——每颗卫星在两个不同的时间进行测量。此外，由于我们事先不知道测量之间的最佳时间间隔（Δt）将是，我们考虑了 Δt 从 1 秒到 101 秒，以 1 秒为增量。（当时间超过 101 秒时，部分或全部卫星可能已经移出视野。）

为了进行比较，我们考虑了恰好有八颗卫星可见的场景，以便可以计算传统的 D-GDOP。我们编写了一个 MATLAB 脚本来计算当佛罗里达州卡纳维拉尔角可以看到八颗卫星时单个轨道内所有时间的D-GDOP。然后，我们为每个星座挑选出 D-GDOP 最高和最低的场景，然后针对每种情况计算 D-GDOPT，使用 8 颗卫星中 4颗卫星的所有 70 种可能组合（假设Δt = 1)。最后，选择出导致 D-GDOPT 最高值和最低值的组合我们编写了一个 MATLAB 脚本来自动计算 D-GDOPT 对于所选的四颗卫星组合在 100 秒范围内 Δt。最低的 D-GDOPT表 1 显示了四种场景下达到的值，以及两个星座的最佳和最坏情况的 D-GDOP 值。总体而言，D-GDOPT措施明显优于最坏情况的 D-GDOP 情景，并且与最佳情况的 D-GDOP 情景相当。

星座	GDOP	最小 D-GDOPT 最佳组合	最小 D-GDOPT 最差组合
OneWeb	25	52	174
OneWeb	3.746	428	1.581
Starlink	9	11	49
Starlink	611	22	26

表 1. 最小 D-GDOPT 最佳和最差四卫星组合的值，与相应的八卫星组合的 D-GDOP 值相比。

在我们进行分析时，我们遇到了一些异常大的 D-GDOP 值，例如针对最坏情况的 OneWeb 场景计算出的 3,746 值。在早期的研究中，由于没有考虑更高的海拔掩模，D-GDOP 分析得出的值要小得多。事实上，我们的分析显示的一些较大的 D-GDOP 值与其他研究人员得出的较小值之间的巨大差异最初让我们停下来思考，随后凸显了使用 Satellite Communications Toolbox 的优势之一。如果我们编写了自己的轨道传播程序来获得 D-GDOP 计算所需的卫星速度和加速度，如此大的差异会让我们质疑我们的实施。在这种情况下，由于我们使用了经过验证的工具箱功能，我们对结果充满信心，并节省了数小时的编程时间和代码审查时间。

作为分析的一部分，我们还仔细研究了 Δt 如何影响 D-GDOPT。我们发现如果 Δt 值较高，D-GDOPT 有时会增加，在某些情况下，最差的组合可能会开始超越最好的卫星组合Δt = 1（图 3）。造成这一现象的原因很复杂。一方面，随着 Δt 的增加，卫星离其初始位置越来越远，从而增加了空间多样性。另一方面，它还改变了卫星相对于地面接收器的速度。需要更好地理解 D-GDOP 计算中位置、速度和加速度矢量之间的相互作用，以找到最佳值 Δt，这是进一步研究的可能途径之一。

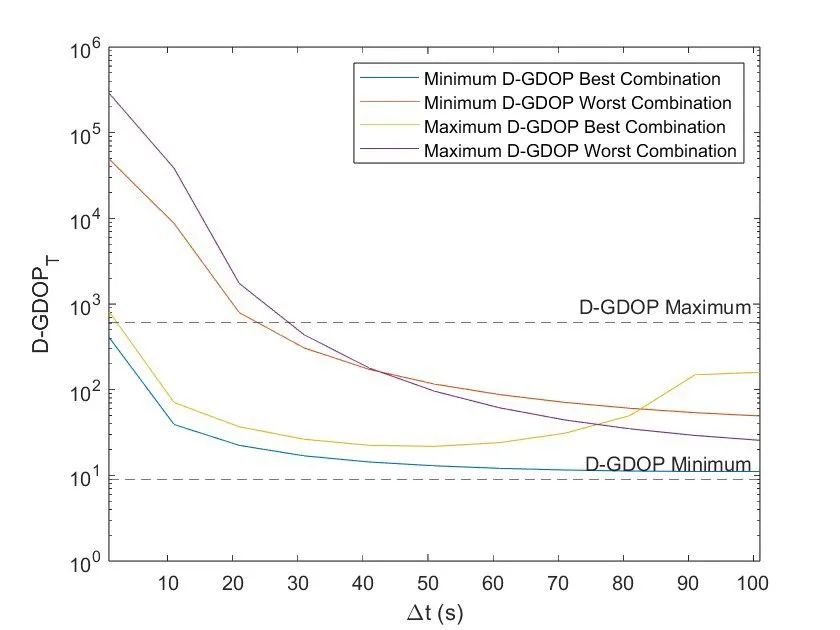
图 3. 在 Δt 范围内D-GDOP T的值的图。

后续步骤

事实证明，当可用的低地球轨道卫星少于八颗时，仅使用多普勒定位是可行的，我们的研究重点正在向多个方向扩展。首先，我们最初的研究仅考虑了固定用户。对于行人来说，用户速度对我们的计算的影响可能很小，但对于飞机和其他高速车辆，我们必须考虑到用户的位置可能会发生很大变化，因为 Δt 增加。

俄亥俄州立大学的 Zak Kassas 博士探索了使用多个星座的卫星，例如结合 OneWeb、Starlink 和Iridium 卫星的测量结果。进一步的研究可能涉及将他的方法与时间多样化方法相结合以进一步提高可用性。此外，我们计划更深入地研究 D-GDOP 最小化策略，可能使用 Global OptimizationToolbox。我们下一步最重要的工作是开发一个完整的模型，该模型能够根据来自少于八颗低地球轨道 (LEO) 卫星的时间差异多普勒测量来确定位置。