在现代通信和信号处理领域,傅里叶变换(FT)扮演着核心角色。它不仅帮助我们分析信号的频率成分,还能用于滤波、压缩和信号恢复等多种任务。
傅里叶变换的基本原理
傅里叶变换是一种将信号从时域转换到频域的数学方法。它基于傅里叶级数的概念,即任何周期函数都可以表示为正弦和余弦函数的和。对于非周期信号,傅里叶变换提供了一种将信号分解为不同频率成分的方法。
应用1:频谱分析
频谱分析是傅里叶变换最直接的应用之一。通过傅里叶变换,我们可以将时间域中的信号转换为频率域中的频谱,从而分析信号的频率成分。这对于识别信号中的周期性成分、噪声水平和信号的带宽等特性至关重要。
应用2:滤波
滤波是信号处理中的一个重要环节,用于去除不需要的频率成分或保留特定的频率范围。傅里叶变换使得滤波操作变得简单,因为我们可以设计滤波器的频率响应,然后通过傅里叶变换将其应用于信号。
应用3:信号压缩
信号压缩技术旨在减少信号的存储或传输所需的数据量。傅里叶变换在信号压缩中扮演着重要角色,尤其是在小波变换和离散余弦变换(DCT)等压缩算法中。通过傅里叶变换,我们可以识别信号中的重要频率成分,并仅保留这些成分以实现压缩。
应用4:信号恢复
在信号传输过程中,信号可能会受到干扰或失真。傅里叶变换可以帮助我们识别和补偿这些失真。通过分析信号的频谱,我们可以设计滤波器来消除或减少干扰,从而恢复信号的原始特性。
应用5:图像处理
傅里叶变换在图像处理领域也有广泛应用,如图像去噪、边缘检测和图像压缩等。通过将图像转换到频率域,我们可以更容易地识别和处理图像中的不同特征。
应用6:语音处理
在语音处理中,傅里叶变换用于语音信号的分析和合成。通过傅里叶变换,我们可以提取语音信号的频谱特征,用于语音识别、语音合成和语音编码等应用。
结论
傅里叶变换是信号处理领域的一项基础技术,它在频谱分析、滤波、压缩、信号恢复等多个方面都有着广泛的应用。随着技术的发展,傅里叶变换的应用领域还在不断扩展,对于提高信号处理的效率和质量起着至关重要的作用。
-
信号处理
+关注
关注
48文章
1041浏览量
103385 -
频率
+关注
关注
4文章
1534浏览量
59347 -
频谱
+关注
关注
7文章
887浏览量
45747 -
傅里叶变换
+关注
关注
6文章
442浏览量
42683
发布评论请先 登录
相关推荐




 傅里叶变换在信号处理中的应用
傅里叶变换在信号处理中的应用

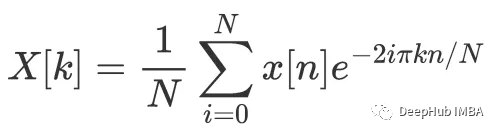










评论