摘要:该文对多无人智能车以领航-跟随法在复杂环境下运动的编队控制问题进行了探讨,通过采用闭环控制律设计了一种编队控制器和编队控制方案,该编队控制器的优点在于其主要考虑智能车之间的距离和角度,同时参考领航者与相邻跟随者之间的信息实现精准控制。
基于所搭建的模拟测试环境,测试改进的控制方法与传统编队方法。实验结果显示,该文所提出的方法在复杂环境下具有更好的运动控制效果。
引言
近三十年来,多无人智能体的协同编队控制方案在多个领域都取得了显著的发展和应用。这是因为在完成一些复杂和困难的任务时,多智能体比单智能体具有更高的鲁棒性和更高的效率。多智能体已经在很多领域得到了极大的重视与应用,如军事探索[1]、海洋水面航行器编队[2]、无人机编队[3]、水下机器人[4]、智能驾驶[5]等。
智能驾驶系统是近年来最为热门的研究领域之一,它分为感知、决策、控制等模块。感知模块通过相机、雷达、全球导航卫星系统等设备来对周围环境进行感知测绘,为智能驾驶系统提供有效的环境信息;决策模块综合环境信息及既定任务进行决策,生成规划路径;控制模块依据生成的路径输出底层的控制量。随着智能驾驶的发展,多无人智能车的协同控制成为了智能驾驶领域的热点问题[5-6]。
解决多无人智能车的协同问题的一种方法是进行编队控制。目前,多无人智能车的协同编队控制方法主要有两大类,分布式协同控制及集中式协同控制。
分布式协同控制指一种没有中心节点控制的结构,通过系统中每个相邻个体之间的通信来实现协调,从而形成完整的编队。它的优点是编队灵活性高、容错性强和易于进行编队控制,缺点是编队稳定性不如集中式协同控制。分布式协同控制方法主要包括基于行为的控制法[7]、领航-跟随控制法[8]和人工势场控制法[9]。
基于行为的控制法的主要思想是,系统根据相应的控制作用产生人类期望的整体系统行为模式,也就是根据想要产生的结果来设计对应的条件与规则。
例如:Lee等[10]基于行为的控制法设计实现了一种可以避障的多智能车的编队。它的优点是可以根据设定的规则完成多种行为,更有利于实时控制;缺点是在复杂环境下对行为规则难以进行清晰的定义,而模糊的行为规则会使系统的不稳定性增加。领航-跟随控制法的主要思想是在一个多智能体的系统中指定其中某个智能体作为领航者,剩余的智能体作为跟随者,跟随者按照领航者的轨迹及设定的编队队形前进。
Jin[11]提出了一种基于视距和角度的编队控制法。它的优点是结构简单、可扩展性强,追随者只需要跟随领航者的轨迹就可以完成系统的整体控制;缺点是当领航者处于复杂环境或者系统的规模过于庞大导致领航者的行为发生错误时,会导致追随者的行为也发生错误,进而导致整个系统崩溃。人工势场控制法的主要思想是设定一个人工势场函数,对系统中的每个个体都施加势场力,从而控制编队。通过势场力来避免碰撞,并保持编队形状。
Gao等[12]设计实现了一种基于人工势场控制法的多智能车编队。它的优点是可以根据系统个体、障碍物模拟出势场力,从而控制系统的下一步运动,实时性强,便于编队控制。人工势场控制法的缺点是在复杂环境中,系统可能会陷入局部最优陷阱,或者在某些较窄的区域无法通行。
集中式协同控制则指拥有系统控制的中心节点,并且系统中每个个体都与中心节点进行通信,从而完成整体的协同,形成完整的编队。它的优点是系统中心节点与系统中个体之间的通信效率高、形成的编队稳定性高,缺点是当中心节点出现故障时,整个系统会陷入崩溃。集中式协同控制方法主要包括基于图论的控制法[13]和虚拟结构控制法[14]。基于图论的控制法的主要思想是以方向图的结构定义系统的编队,以图中的一个节点作为系统中的一个智能体,以节点之间的方向来表示系统中各个智能体之间的位置与方向。基于图论的控制法的优点是系统的稳定性和扩展性强,可以轻易地增加或减少系统节点,所以可以用在大规模的编队中。它的缺点是系统之间的节点通信复杂,实现困难。虚拟结构控制法的主要思想是将整个智能体系统看作是一个刚体的虚拟结构,将系统中的每个智能体作为虚拟结构中的一个固定的点[15]。虚拟结构控制法的优点是系统结构的稳定性强,易于保持系统的编队;缺点是缺少局部节点的控制,在复杂环境中,对障碍物的躲避有一定的局限性。
为了在复杂环境下实现一个结构简单、灵活,扩展编队方便、迅速,且具有一定避障能力的编队控制,综合上面的讨论进行以下分析。集中式协同控制方法构建更加复杂,且在复杂环境中的效果也不一定理想。相比之下,分布式协同控制中的领航-跟随控制法的结构较为简单,容错性高、可扩展性强,且灵活性强,更加适应在复杂环境中完成预定任务。
本文的结构如下:第2节表述相关问题;第3节介绍本文的设计;第4节介绍仿真结果;第5节总结本文。
问题提出与准备
2.1 无人智能车运动模型描述
为简单建立一个无人智能车运动模型,并且尽可能保证建立的运动模型与真实车辆模型的特性相似,本文采用自行车模型(Bicycle Model)[16],这是一种较为符合真实车辆模型特性的运动学模型,并且以智能车的一个前向轮为代表,作为建立运动模型的基准。图1为车辆运动模型。
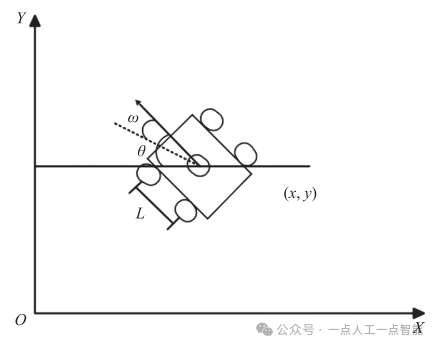
图1 车辆运动模型
若要使用自行车模型来代表智能车的运动模型,则需要对车辆模型做出以下假设:
(1)车辆模型仅考虑二维平面内的运动,而忽略三维平面的运动。即仅考虑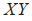 轴上的运动,而不考虑
轴上的运动,而不考虑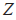 轴上的运动;
轴上的运动;
(2)假定该智能车的左右两个前轮的转向角度是完全一致的,那么就可以由智能车的一个前向轮表示智能车的两个车轮的运动控制,从而搭建起自行车模型;
(3)智能车不会形变,即保证智能车的车身是刚性的;
(4)智能车的后轴及两个后轮不会对整个智能车产生影响。
如图2所示,建立的运动学模型将智能车的左右两个前轮合并为一个轮子,并将这个轮子平移到小车的中心位置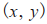 ,作为该智能车在该坐标系中的参考位置,在以
,作为该智能车在该坐标系中的参考位置,在以 为坐标原点的世界坐标系中定义智能车的位置姿态信息为:
为坐标原点的世界坐标系中定义智能车的位置姿态信息为:

其中,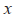 为智能车的前轮中心点在坐标轴
为智能车的前轮中心点在坐标轴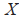 轴方向的坐标;
轴方向的坐标;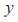 为智能车的前轮中心点在坐标轴
为智能车的前轮中心点在坐标轴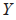 轴方向的坐标;
轴方向的坐标;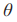 为智能车的前进方向;
为智能车的前进方向;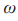 为前轮转向角度。
为前轮转向角度。
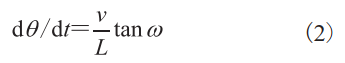
其中,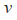 为智能车前进的速度;
为智能车前进的速度;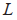 为智能车前后轮的距离。
为智能车前后轮的距离。
若已知智能车的线速度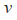 和前轮转向角度
和前轮转向角度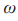 ,则可以得到:
,则可以得到:

对公式(1)进行求导,并将公式(2)~(3)带入,可得智能车的运动模型:

为了得到智能车的简化规范模型,可以假设智能车转向的速度足够快,从而使车辆的转向角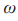 瞬间改变,那么
瞬间改变,那么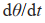 就可以被消除,从而可以得到智能车的简化规范模型:
就可以被消除,从而可以得到智能车的简化规范模型:
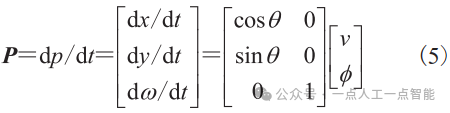
由于希望建立的模型是一个简单、尽可能与真实车辆模型的特性相似的智能车的运动模型,所以需要对智能车模型施加以下约束条件:
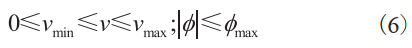
2.2 领航-跟随模型
针对第2.1小节所建立的智能车的运动学模型,本节建立了一个领航者-跟随者编队的运动模型。同样地,以智能车的前轮中心的位置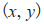 来代表智能车的位置坐标,以
来代表智能车的位置坐标,以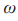 表示领航智能车的转向角度,
表示领航智能车的转向角度,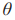 表示领航者和跟随者之间的夹角,
表示领航者和跟随者之间的夹角,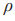 表示领航者和跟随者中心之间的距离。以无人智能车的前轮中心
表示领航者和跟随者中心之间的距离。以无人智能车的前轮中心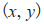 作为智能车在该坐标系中的参考位置,以
作为智能车在该坐标系中的参考位置,以 为坐标原点建立世界坐标系。在该坐标系中,领航者的位置坐标信息为
为坐标原点建立世界坐标系。在该坐标系中,领航者的位置坐标信息为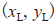 ,跟随者的位置坐标信息为
,跟随者的位置坐标信息为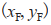 ,如图2所示。
,如图2所示。
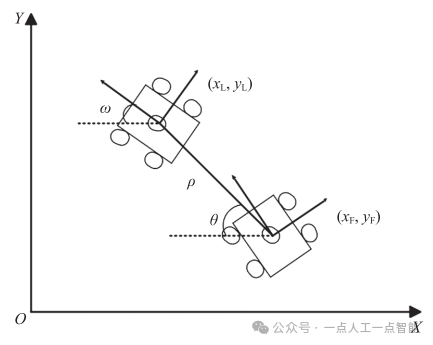
图2 领航-跟随简易模型
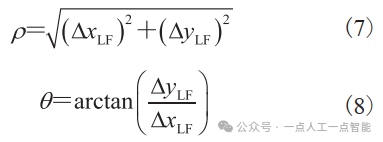
其中,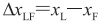 ;
;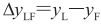 。
。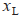 为领航者在建立的坐标系中的
为领航者在建立的坐标系中的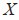 轴上的坐标,
轴上的坐标,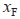 为跟随者在建立的坐标系中的
为跟随者在建立的坐标系中的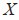 轴上的坐标。
轴上的坐标。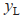 为领航者在建立的坐标系中的
为领航者在建立的坐标系中的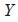 轴上的坐标,
轴上的坐标,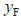 为跟随者在建立的坐标系中的
为跟随者在建立的坐标系中的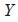 轴上的坐标。在公式(8)中,该函数
轴上的坐标。在公式(8)中,该函数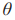 的范围为
的范围为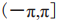 。
。
如图2所示,本文中建立的领航者-追随者编队的运动模型基于领航者和追随者之间的距离和角度。因此,将产生的距离和角度写作向量形式:
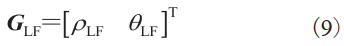
期望产生的距离和角度的向量是
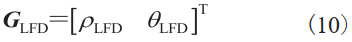
若想让跟随者保持稳定的编队,就需要设计产生一个控制输入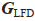 ,并使跟随者编队的跟踪误差尽可能小。
,并使跟随者编队的跟踪误差尽可能小。
2.3 存在的问题
Das等[17]提出了两种反馈控制方法: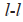 控制和
控制和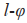 控制。这是领航跟随法中最流行的控制方法之一。
控制。这是领航跟随法中最流行的控制方法之一。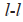 控制方法:该控制方法的目的在于控制某一智能体与其关联的多个智能体之间的相对位移和角度,并使该位移和角度数值保持不变。
控制方法:该控制方法的目的在于控制某一智能体与其关联的多个智能体之间的相对位移和角度,并使该位移和角度数值保持不变。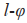 控制方法:该控制方法的目的在于控制各智能体之间的相对位移和角度,并使其最终收敛到某一期望数值。显然,这两种控制方法都需要知道跟随者和领航者之间的距离和角度。根据距离信息分析,Kang等[18]提出了一种基于距离信息的编队控制方法。根据角度信息分析,Trinh等[19]提出了一种基于角度信息的编队控制方法。根据距离-角度信息分析,Jin[11]提出了一种基于距离-角度信息的编队控制方法。
控制方法:该控制方法的目的在于控制各智能体之间的相对位移和角度,并使其最终收敛到某一期望数值。显然,这两种控制方法都需要知道跟随者和领航者之间的距离和角度。根据距离信息分析,Kang等[18]提出了一种基于距离信息的编队控制方法。根据角度信息分析,Trinh等[19]提出了一种基于角度信息的编队控制方法。根据距离-角度信息分析,Jin[11]提出了一种基于距离-角度信息的编队控制方法。
上述方法存在一个问题,即当系统中缺乏明确的反馈控制信息或反馈控制信息出错时,如果领航者发生错误行为,则会直接导致跟随智能体的行为紊乱,从而使整个系统陷入崩溃状态。例如,如果领航智能体的移动速度过快或移动距离超出跟随智能体的跟踪范围,则会出现跟随智能体掉队的现象。在复杂环境中,这种情况极易发生,从而导致多智能车的编队被破坏,系统陷入崩溃。
改进的控制方案
领航跟随法是多车编队控制算法中发展得比较成熟的算法,它在编队控制方面有着广泛的应用。领航跟随法中基于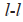 的编队控制方法只以智能车之间的相对距离作为控制的主要参数依据,这种方法的编队方式不够灵活,并且至少需要选择两个领航者对其进行控制输入,增加了系统的计算复杂度。领航跟随法中基于
的编队控制方法只以智能车之间的相对距离作为控制的主要参数依据,这种方法的编队方式不够灵活,并且至少需要选择两个领航者对其进行控制输入,增加了系统的计算复杂度。领航跟随法中基于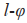 的编队控制方法只需要选择一个领航者,跟随者根据与领航者之间的相对距离和角度的设定进行移动,从而实现所期望的队形的编队控制。相比之下,基于
的编队控制方法只需要选择一个领航者,跟随者根据与领航者之间的相对距离和角度的设定进行移动,从而实现所期望的队形的编队控制。相比之下,基于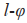 的编队控制方法在编队形式上更加灵活。因此,结合第2.3小节所提出的问题,本文在
的编队控制方法在编队形式上更加灵活。因此,结合第2.3小节所提出的问题,本文在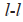 的编队控制方法和
的编队控制方法和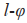 的编队控制方法的基础上将这两种方法相结合,并利用闭环控制方法设计了一种多车编队控制方案。
的编队控制方法的基础上将这两种方法相结合,并利用闭环控制方法设计了一种多车编队控制方案。
这种基于闭环控制方法的多车编队方案通过维持领航者与跟踪者之间的相对距离与相对角度不发生变化,使智能车的队形保持期望的队形,并维持稳定。多车编队闭环控制方案如图3所示。
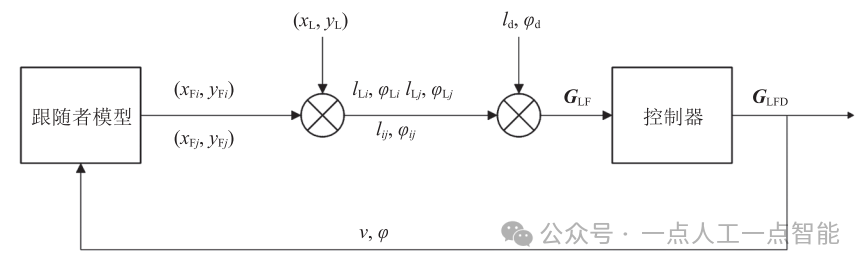
图3 多车编队闭环控制方案
如图3所示,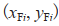 表示跟随者
表示跟随者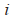 的位置,
的位置,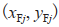 表示跟随者
表示跟随者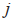 的位置。
的位置。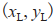 代表领航者的位置。
代表领航者的位置。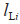 表示领航者与跟随者
表示领航者与跟随者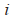 之间的相对距离,
之间的相对距离,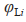 表示领航者与跟随者
表示领航者与跟随者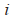 之间的相对角度,
之间的相对角度,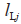 表示领航者与跟随者
表示领航者与跟随者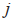 之间的相对距离,
之间的相对距离,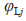 表示领航者与跟随者
表示领航者与跟随者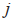 之间的相对角度。
之间的相对角度。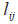 表示跟随者
表示跟随者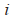 和跟随者
和跟随者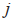 之间的相对距离,
之间的相对距离,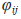 表示跟随者
表示跟随者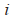 和跟随者
和跟随者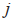 之间的相对角度。
之间的相对角度。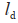 表示系统预先设定好的相对距离,
表示系统预先设定好的相对距离,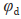 表示系统预先设定好的相对角度。
表示系统预先设定好的相对角度。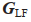 是产生的控制输入向量,
是产生的控制输入向量,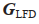 是经过控制器调整后的控制输入变量。
是经过控制器调整后的控制输入变量。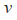 是输出的速度控制,
是输出的速度控制,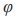 是输出的角度控制。
是输出的角度控制。
闭环控制是控制论的一个概念,指具有反馈信息的系统控制方式。在闭环控制系统中,系统运行时会将控制信息传递给受控对象,并将受控对象的状态信息反馈到输入端,用于修正操作过程,使系统输出符合预期要求[20-21]。图3展示了闭环控制方法在设计的编队控制器中的应用。跟随者通过计算自身与领航者以及与相邻智能车之间的位置,得出实际的相对距离和角度。然后,根据系统中预设的相对距离和角度,经过控制器的调整输出速度和角度的控制参数,使得跟随者可以根据领航者和相邻跟随者的位置来调整自身的位置和姿态,从而形成完整稳定的编队。
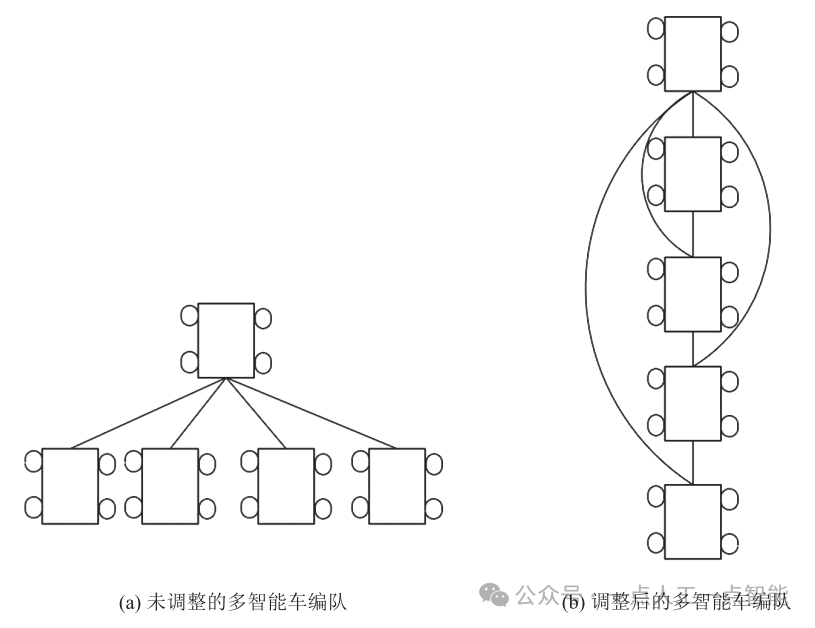
图4 多智能车编队队形比较
图4(a)展示的是未调整的多智能车编队,图4(b)展示的是调整后的多智能车编队。
结果
本节在Gazebo中搭建3个模拟场景来测试提出的改进控制方法。第一种模拟场景,空白场地。第二种模拟场景,有单个障碍物的开阔场地。第三种模拟场景,有多个障碍物的狭窄场地。
图5(a)展示的是未调整的编队运动效果,图5(b)展示的是调整后的编队运动效果。在图5(a)~(b)中,L表示领航者,1、2、3、4表示4个追随者。图5(c)展示了未调整的编队中,领航者与跟随者之间的距离,图5(d)展示了调整后的编队中,领航者与跟随者之间的距离。在图5(c)~(d)中,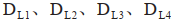 分别表示1、2、3、4四个追随者与领航者
分别表示1、2、3、4四个追随者与领航者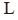 之间的距离。从图5(c)~(d)可以看出,在空白场地的环境下,经过一段时间后,两种编队的领航者与跟随者都保持了稳定的距离。这表明这两种编队的运动效果都很好,可以在空旷环境中形成稳定的编队。
之间的距离。从图5(c)~(d)可以看出,在空白场地的环境下,经过一段时间后,两种编队的领航者与跟随者都保持了稳定的距离。这表明这两种编队的运动效果都很好,可以在空旷环境中形成稳定的编队。
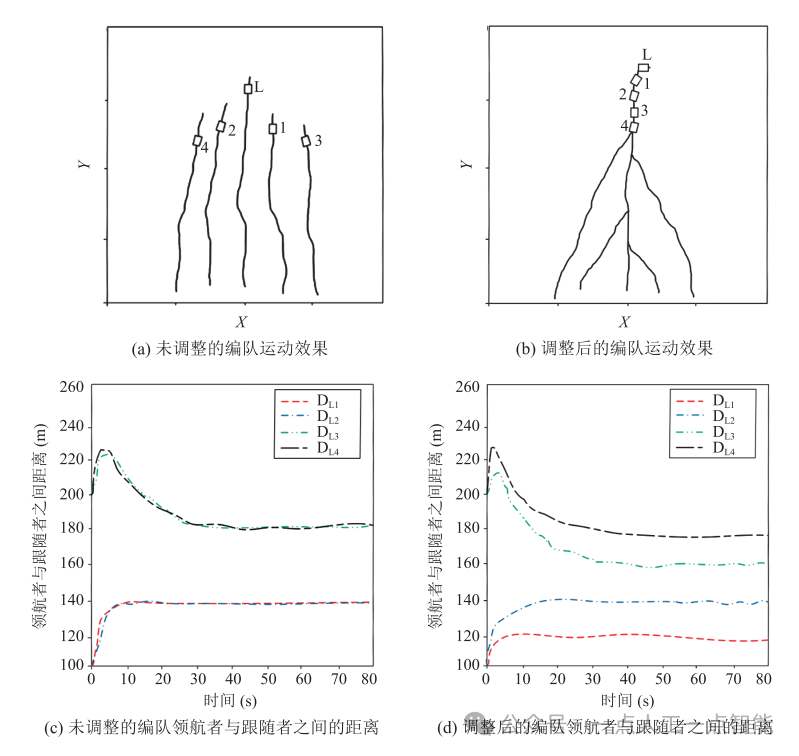
图5 空白场地测试效果
图6展示了编队在单障碍物环境中的运动效果,图6(a)~(b)中黑色区域为障碍物,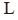 表示领航者,1、2、3、4表示4个追随者。通过图6(c)~(d)可以看出,在障碍物较少的环境下,两种编队仍然可以保持稳定的距离,形成较好的编队控制效果。
表示领航者,1、2、3、4表示4个追随者。通过图6(c)~(d)可以看出,在障碍物较少的环境下,两种编队仍然可以保持稳定的距离,形成较好的编队控制效果。
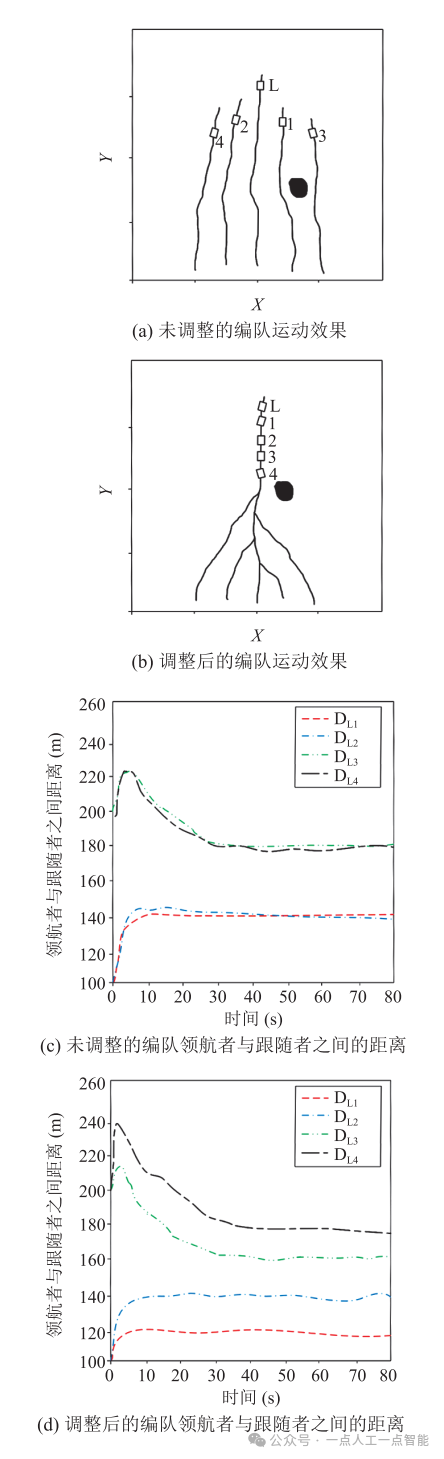
图6 单障碍物场地测试效果
图7展示了编队在多障碍物环境中的运动效果。从图7(a)可以看到,在未调整的编队中,跟随者1、2都被障碍物挡住。从图7(c)中可以看出,跟随者3、4与领航者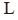 之间的距离仍然保持稳定,而跟随者1、2与领航者
之间的距离仍然保持稳定,而跟随者1、2与领航者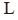 之间的距离不断增大。从图7(d)中可以看出,在调整后的编队中,跟随者与领航者之间的距离仍然保持稳 定。这表明调整后的编队在多障碍物环境中的运动效果更好,比传统编队控制更加适合在相对复杂的环境中运行。
之间的距离不断增大。从图7(d)中可以看出,在调整后的编队中,跟随者与领航者之间的距离仍然保持稳 定。这表明调整后的编队在多障碍物环境中的运动效果更好,比传统编队控制更加适合在相对复杂的环境中运行。
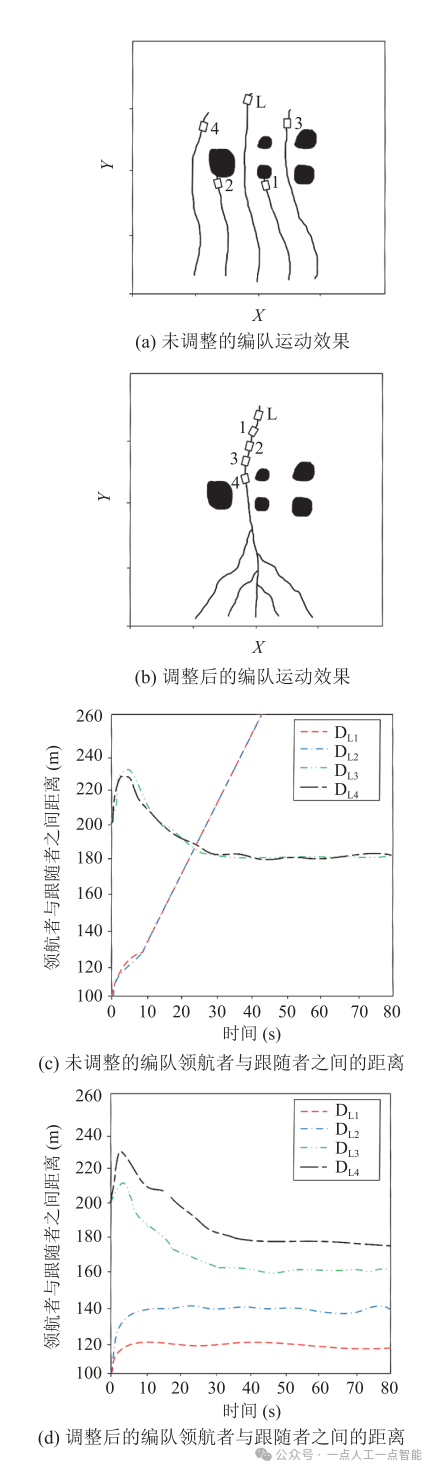
图7 多障碍物场地测试效果
图8(a)展示的是期望输出速度与实际输出速度,图8(b)展示的是期望输出角度与实际输出角度。在图8(a)~(b)中,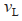 为领航者
为领航者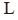 的速度,
的速度,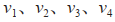 分别表示输出给跟随者的实际速度,
分别表示输出给跟随者的实际速度,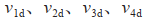 分别表示输出给跟随者的期望速度。
分别表示输出给跟随者的期望速度。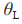 为领航者的转向角度,
为领航者的转向角度,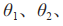
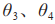 分别为输出给跟随者的实际角度,
分别为输出给跟随者的实际角度,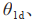
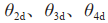 分别为输出给跟随者的期望角度。从图8(a)~(b)中可以看出,跟随者经过几秒后可以捕捉到领航者的运动,并且期望输出的速度 和角度与实际输出的速度和角度有些许偏差。这些偏差可能是系统本身的误差、传感器的不准确性或环境干扰等因素导致的。未来的研究可以针对这些偏差进行优化和改进,使系统能够更好地适应复杂环境和变化的任务需求。
分别为输出给跟随者的期望角度。从图8(a)~(b)中可以看出,跟随者经过几秒后可以捕捉到领航者的运动,并且期望输出的速度 和角度与实际输出的速度和角度有些许偏差。这些偏差可能是系统本身的误差、传感器的不准确性或环境干扰等因素导致的。未来的研究可以针对这些偏差进行优化和改进,使系统能够更好地适应复杂环境和变化的任务需求。
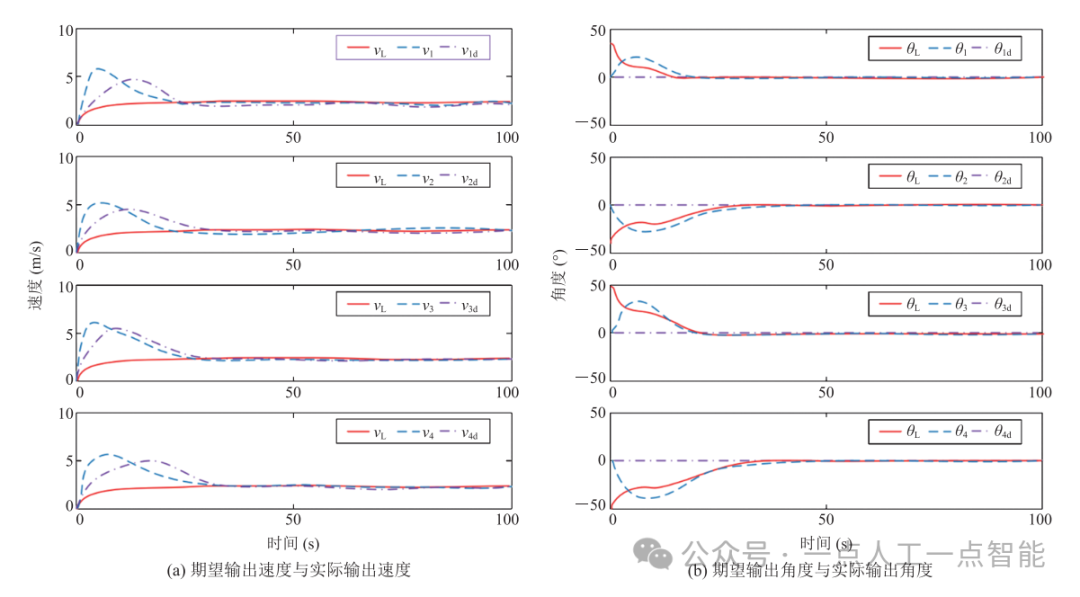
图8 期望输出与实际输出
结论
本文提出了一种将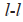 的编队控制方法和
的编队控制方法和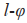 的编队控制方法相结合的编队控制方案,并设计了一种编队控制器,用于系统中不存在明确的反馈控制信息或反馈控制信息出错时的多智能车的编队控制。与现有的编队控制方案相比,所提出的这种编队方法在复杂环境中效果更好。仿真结果表明,所设计的编队控制器是有效的;在相对复杂环境下,这种方法的编队灵活性更好。
的编队控制方法相结合的编队控制方案,并设计了一种编队控制器,用于系统中不存在明确的反馈控制信息或反馈控制信息出错时的多智能车的编队控制。与现有的编队控制方案相比,所提出的这种编队方法在复杂环境中效果更好。仿真结果表明,所设计的编队控制器是有效的;在相对复杂环境下,这种方法的编队灵活性更好。
-
控制器
+关注
关注
112文章
16316浏览量
177788 -
智能车
+关注
关注
21文章
403浏览量
76949
原文标题:复杂环境中多无人智能车协同控制
文章出处:【微信号:vision263com,微信公众号:新机器视觉】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
智能车
基于光电导航的无人驾驶智能车
超高频RFID智能车辆管理系统的工作原理是什么?
怎么实现移动智能车辆稽查系统的设计?
基于RFID的智能车辆管理系统
虚拟计算环境中的多机群协同调度算法

多无人机协同编队飞行控制的关键技术和发展展望

世界智能车辆的关键共性技术研究现状
多无人机局部地图数据共享融合的SLAM方法
基于无线自组网的多无人机系统解决方案
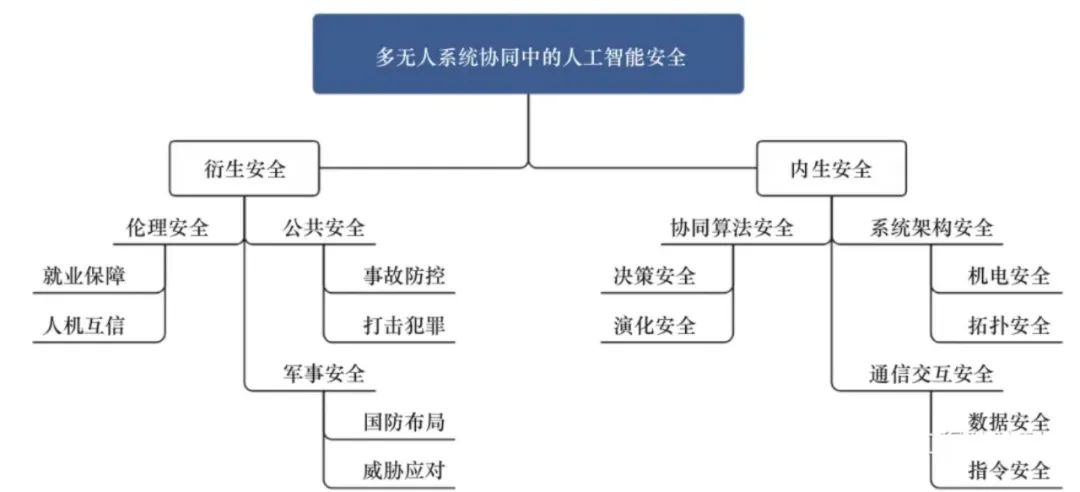
陈杰院士:多无人系统协同中的人工智能安全探索




 复杂环境下多无人智能车辆协同调控
复杂环境下多无人智能车辆协同调控










评论