K-means的优缺点及改进

K-means算法是很典型的基于距离的聚类算法，采用距离作为相似性的评价指标，即认为两个对象的距离越近，其相似度就越大。该算法认为簇是由距离靠近的对象组成的，因此把得到紧凑且独立的簇作为最终目标。

k个初始类聚类中心点的选取对聚类结果具有较大的影响，因为在该算法第一步中是随机的选取任意k个对象作为初始聚类的中心，初始地代表一个簇。该算法在每次迭代中对数据集中剩余的每个对象，根据其与各个簇中心的距离将每个对象重新赋给最近的簇。当考察完所有数据对象后，一次迭代运算完成，新的聚类中心被计算出来。如果在一次迭代前后，J的值没有发生变化，说明算法已经收敛。

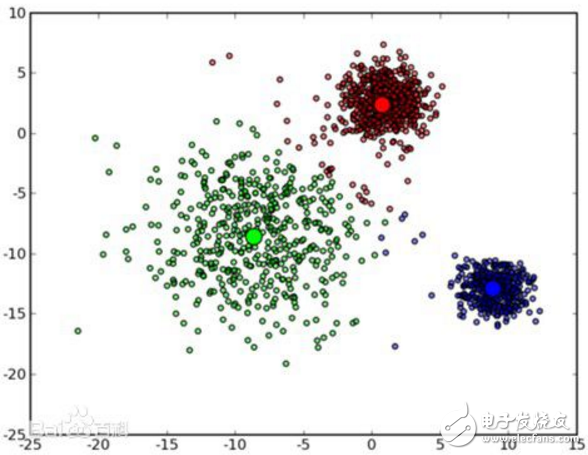
算法过程如下：

1）从N个文档随机选取K个文档作为质心

2）对剩余的每个文档测量其到每个质心的距离，并把它归到最近的质心的类

3）重新计算已经得到的各个类的质心

4）迭代2～3步直至新的质心与原质心相等或小于指定阈值，算法结束

具体如下：

输入：k， data［n］;

（1） 选择k个初始中心点，例如c［0］=data［0］，…c［k-1］=data［k-1］；

（2） 对于data［0］….data［n］，分别与c［0］…c［k-1］比较，假定与c［i］差值最少，就标记为i；

（3） 对于所有标记为i点，重新计算c［i］={ 所有标记为i的data［j］之和}/标记为i的个数；

（4） 重复（2）（3），直到所有c［i］值的变化小于给定阈值。

Kmeans算法的优缺点

K-means算法的优点是：首先，算法能根据较少的已知聚类样本的类别对树进行剪枝确定部分样本的分类；其次，为克服少量样本聚类的不准确性，该算法本身具有优化迭代功能，在已经求得的聚类上再次进行迭代修正剪枝确定部分样本的聚类，优化了初始监督学习样本分类不合理的地方；第三，由于只是针对部分小样本可以降低总的聚类时间复杂度。

K-means算法的缺点是：首先，在 K-means 算法中 K 是事先给定的，这个 K 值的选定是非常难以估计的。很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适；其次，在 K-means 算法中，首先需要根据初始聚类中心来确定一个初始划分，然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响，一旦初始值选择的不好，可能无法得到有效的聚类结果；最后，该算法需要不断地进行样本分类调整，不断地计算调整后的新的聚类中心，因此当数据量非常大时，算法的时间开销是非常大的。

K-means算法对于不同的初始值，可能会导致不同结果。解决方法：

1.多设置一些不同的初值，对比最后的运算结果，一直到结果趋于稳定结束

2.很多时候，事先并不知道给定的数据集应该分成多少个类别才最合适。通过类的自动合并和分裂，得到较为合理的类型数目 K，例如 ISODATA 算法。

K-means算法的其他改进算法如下：

1. k-modes 算法：实现对离散数据的快速聚类，保留了k-means算法的效率同时将k-means的应用范围扩大到离散数据。

2. k-Prototype算法：可以对离散与数值属性两种混合的数据进行聚类，在k-prototype中定义了一个对数值与离散属性都计算的相异性度量标准。

大家接触的第一个聚类方法，十有八九都是K-means聚类啦。该算法十分容易理解，也很容易实现。其实几乎所有的机器学习和数据挖掘算法都有其优点和缺点。

（1）对于离群点和孤立点敏感；

（2）k值选择;

（3）初始聚类中心的选择；

（4）只能发现球状簇。

对于这4点呢的原因，读者可以自行思考下，不难理解。针对上述四个缺点，依次介绍改进措施。

改进1

首先针对（1），对于离群点和孤立点敏感，如何解决？提到过离群点检测的LOF算法，通过去除离群点后再聚类，可以减少离群点和孤立点对于聚类效果的影响。

改进2

k值的选择问题，在安徽大学李芳的硕士论文中提到了k-Means算法的k值自适应优化方法。下面将针对该方法进行总结。

首先该算法针对K-means算法的以下主要缺点进行了改进：

1）必须首先给出k（要生成的簇的数目），k值很难选择。事先并不知道给定的数据应该被分成什么类别才是最优的。

2）初始聚类中心的选择是K-means的一个问题。

李芳设计的算法思路是这样的：可以通过在一开始给定一个适合的数值给k，通过一次K-means算法得到一次聚类中心。对于得到的聚类中心，根据得到的k个聚类的距离情况，合并距离最近的类，因此聚类中心数减小，当将其用于下次聚类时，相应的聚类数目也减小了，最终得到合适数目的聚类数。可以通过一个评判值E来确定聚类数得到一个合适的位置停下来，而不继续合并聚类中心。重复上述循环，直至评判函数收敛为止，最终得到较优聚类数的聚类结果。

改进3

对初始聚类中心的选择的优化。一句话概括为：选择批次距离尽可能远的K个点。具体选择步骤如下。

首先随机选择一个点作为第一个初始类簇中心点，然后选择距离该点最远的那个点作为第二个初始类簇中心点，然后再选择距离前两个点的最近距离最大的点作为第三个初始类簇的中心点，以此类推，直至选出K个初始类簇中心点。

对于该问题还有个解决方案。之前我也使用过。熟悉weka的同学应该知道weka中的聚类有一个算法叫Canopy算法。

选用层次聚类或者Canopy算法进行初始聚类，然后利用这些类簇的中心点作为KMeans算法初始类簇中心点。该方法对于k值的选择也是十分有效的。

改进4

只能获取球状簇的根本原因在于，距离度量的方式。在李荟娆的硕士论文K_means聚类方法的改进及其应用中提到了基于2种测度的改进，改进后，可以去发现非负、类椭圆形的数据。但是对于这一改进，个人认为，并没有很好的解决K-means在这一缺点的问题，如果数据集中有不规则的数据，往往通过基于密度的聚类算法更加适合，比如DESCAN算法。