随着系统功能的日益复杂,以自适应控制为代表的先进控制理论与算法越来越多地被投入到工程应用当中。而随着大家对被控物理系统特性本身和控制理论更加深入的研究,像鲁棒控制、模型预测控制、模糊逻辑控制,甚至是强化学习,都逐渐成为了控制工程师口袋中的武器。
然而对于传统的嵌入式应用而言,成本上的考量使得硬件算力的进一步提升成为一种奢望,也从一定程度上限制了更加“智能”的控制算法的应用。例如在自动驾驶或者自主系统控制领域颇为流行的非线性模型预测控制,很难直接应用于算力更加紧张,但也更广泛的传统嵌入式场景当中,工程师们也只能去选择更加“简化”的控制算法来实现部署,这也是为什么在传统的嵌入式控制场景中,基于经典线性控制理论的PID 控制器依然很流行。
但随着被控对象系统的动态越来越复杂,其非线性程度、外部扰动和不确定性越来越高,PID 明显力不从心。相比于直接使用类似非线性模型预测控制这类运算复杂、对硬件算力要求极高的控制算法,工程师们开始越来越多地探索如何在传统 PID 控制中添加一些“自适应”因素,让其能够在有限的硬件资源限制下,尽可能地响应和处理真实物理系统中的未知干扰与不确定性,从而也能达到更好的控制效果。
MathWorks 作为工具厂商也在积极响应用户类似的需求,在过去的几个版本中,陆续添加了诸如模型参考自适应控制、自抗扰控制和模型预测控制等功能(详见之前的文章《让闭环控制器的参数调节事半功倍-SimulinkControl Design更新探讨》)。在今天的文章中,我们将重点讨论在24b 版本中新添加的滑模控制(Sliding Mode Control, SMC)模块支持以及相关案例。
滑模控制(SMC)是一种以其鲁棒性和高效性著称的非线性控制策略。自 20 世纪 50 年代首次提出以来,滑模控制因其在处理不确定性系统和外部扰动方面的卓越性能,逐渐成为自动控制领域的重要研究方向。滑模控制的最大优势在于其对系统参数变化和外部干扰的强鲁棒性,这使得它在实际应用中能够有效应对各种不确定性(包括不限于系统的非线性特性、外部扰动等等)。此外,滑模控制结构简单,易于实现,且能够提供快速的动态响应,在传统嵌入式应用硬件算力受限的情况下依然适用。在现代控制系统中,滑模控制被广泛应用于电机控制、机器人系统、车辆动态控制以及航空航天等领域。
滑模控制原理概述
听起来滑模控制无所不能是不是?它是如何保证上述这些优势的?这就需要简单介绍一下它的原理。
滑模控制是一种特殊的变结构控制,它与常规控制的区别在于控制的不连续性,其核心思想是根据系统所期望的动态特性来设计一个滑模面(Sliding Surface),通过控制器使系统状态从滑模面之外向其快速收敛并保持在该面上。系统一旦到达滑模面,控制器通过反馈控制将保证系统沿该面到达系统原点(目标稳态工况)。由于系统的特性和参数只取决于设计的滑模面而与外界干扰没有关系,所以滑模控制具有很强的鲁棒性。
文字看起来比较绕?我们用下面的公式来帮助理解。
考虑用如下公式表征的一般非线性系统,
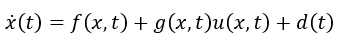
其中,代表系统固有的动态特性,代表控制输入对系统的影响,则反应了随时间影响系统行为的外部干扰。
该公式反映了系统本身的动态特性,控制输入和外部未知干扰的耦合。如前面我们提到的,SMC 是一种变结构的控制,其在两种不同的结构之间切换,从数学上描述为:
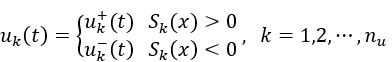
在这里,我们分别定义了两组不同的控制输入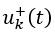 和
和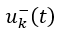 ,分别用于系统处于滑模面的不同侧。假设系统有 nu 个控制输入,则 nu 个 Sk 便可以组成滑模面函数 S(x)。
,分别用于系统处于滑模面的不同侧。假设系统有 nu 个控制输入,则 nu 个 Sk 便可以组成滑模面函数 S(x)。
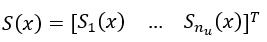
为了保证状态变量能够收敛于滑模面,并保持其轨迹始终沿着滑模面,合理设计控制输入u和滑模面S(x)至关重要。当系统状态到达滑模面后,滑模面函数能够满足S(x)=0,要使得如前述公式所示的一般非线性系统能够达到并稳定在滑模面中,我们必须要求滑模面与其导数满足如下关系:
我们可以用如下的平面图来解释这样的关系,假设图中的直线表示滑模面S(x),其导数必须与S(x)呈相反的符号,才能保证系统状态稳定在S(x)上。
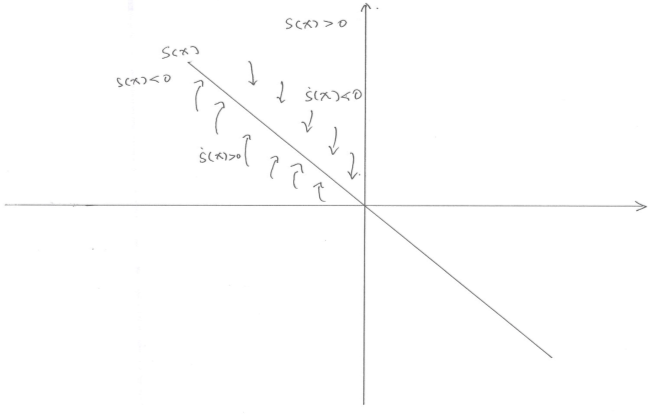
图1 滑模面的二维等效解释
那么如何来快速定义控制输入和滑模面呢?显然如果没有工具加持,大多数情况下我们依然无从下手。在最新的 MATLAB R2024b 版本中,用户可以使用 SlidingMode Controller (Reaching Law)[1]模块,使用一种动态调整控制动作(趋近率,ReachingLaw)以有效地将系统状态引导到滑模面,从而实现滑模控制。在该模块中,我们支持两类滑动模态模式,以帮助用户快速定义滑模面函数和控制输入。
第一类:调节模式,当我们希望将系统稳定在一个固定工况点时使用此模式,此时系统的所有状态变量 x为零,
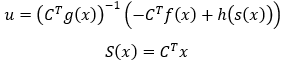
第二类,跟踪模式,通常情况下,闭环控制希望的是让系统的状态跟随一个参考的轨迹指令 xref。
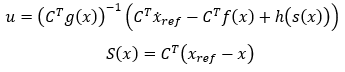
易见,第一类问题是第二类问题的一种特殊情况。在上述公式中,滑动系数矩阵 C决定了滑模面S(x)的形状,我们可以用它来定义滑模面 S(x)。h(s(x)) 则被叫做趋近率(Reaching Law),它表征了系统以什么样的动态特性收敛并保持在滑模面上,我们用它来定义控制输入 u,Reaching Law 有几种不同的方式,在现有模块中提供了三种方式:
恒定速率(Constant rate):系统以恒定速率达到滑模面,较大的恒定速率可以使得系统更快地收束到滑模面,但可能会引发执行器控制饱和或者控制不稳定。
指数速率(Exponential):通过给恒定速率添加比例增益项以避免恒定速率引发的问题,比例增益项使得系统状态偏离滑模面较大时提供更快的收敛速率,而在偏差变小时作用减弱。
功率比(Power Rate):不同于固定常数的比例增益,通过增加一个0到1之间的系数 来平滑调节系统状态与滑模面偏差不同时的收敛速度,以兼顾收敛速度和平稳性。
典型案例分析之一弹簧阻尼系统
公式介绍完了,相信大家能够了解滑模控制的基本原理,知道在滑模控制中,最重要的是定义滑模面S(x)和控制输入 u,也知道 MATLAB/Simulink 现在有“即插即用”的模块来帮助我们定义。但如果要向其它人解释什么滑模面S(x),以及如何通过调节它来提升滑模控制的性能,作者在写到这里的时候也跟大家一样都是一头雾水。因为相比于那些传统的控制理论,这个不是平面,却又叫做“面” S(x)的实在是太过抽象,干凭冥想理解它着实不容易。我们需要一个简单的物理场景来具像化它,帮助我们理解。在 MATLAB R2024b的帮助文档中就给出这样一个例子,SlidingMode Control Design for Mass-Spring-Damper System[2],下面就让我们一起来探讨一下。
我们考虑如下一个简单的质量-弹簧-阻尼系统,视为质点的质量为 M 的质量块,在弹性系数为 K,阻尼系数为 D 的约束下,被大小为 F 的力驱动(视为控制输入)。
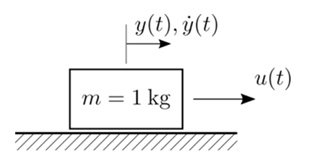
图2 质量-弹簧-阻尼系统示例
我们可以很轻易地得到反映其动态的系统方程,
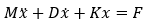
其中,x 代表质量块的横向位移,即图中的y,那么 x ̇和 x自然代表它的速度和加速度。
等一下,这个系统动态的方程跟我们一开始定义的一般非线性系统表征不太一样,为了保持一致,我们需要先做一些修改,
我们在系统中定义两个变量,横向位移为 x₁,速度为 x₂,则系统动态可以表示为
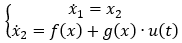
其中,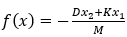 ,
,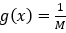 。 为何选了这样一个系统?因为如果我们将系统中的两个状态分别置于平面坐标系的横轴和竖轴上,它就会形成一个“平面”。
。 为何选了这样一个系统?因为如果我们将系统中的两个状态分别置于平面坐标系的横轴和竖轴上,它就会形成一个“平面”。
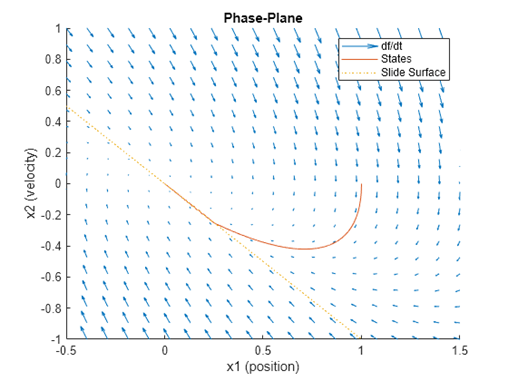
图3 质量-弹簧-阻尼系统相平面
由图上我们可以知道,系统的“轨迹”(两个状态变量的变化),永远是跟随着图中蓝色的箭头来行进,即位移绝对值达到最大值时,速度都是零。那么在图中,我们可以找到这样一条分割线,x₁+x₂= 0,无论当系统的工作状态处于分割线左边或者右边时,都会向这条线“收敛。”
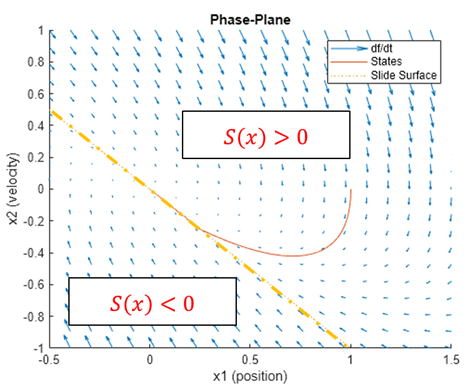
图4 质量-弹簧-阻尼系统滑模面
显然,图中这条线就满足之前我们对滑模面S(x)的讨论,在这个例子中,我们便可以定义S(x)=x₁+x₂,此时滑模系数矩阵 C=[11]ᵀ。
在定义好滑模面S(x)之后,我们只需要确定滑模控制器的滑动模态方式以及趋近率方式,即可确定控制输入 u。我们希望系统能够在任何的外部干扰作用下,质量滑块都能沿着滑模面稳定在原点附近,所以我们选择“调节模式”作为滑动模态方式,并选择指数速率作为趋近率。
当然这些设置在 MATLAB 中都非常容易实现,只需要在 Sliding ModeController (Reaching Law) 模块的对应位置给定参数即可。
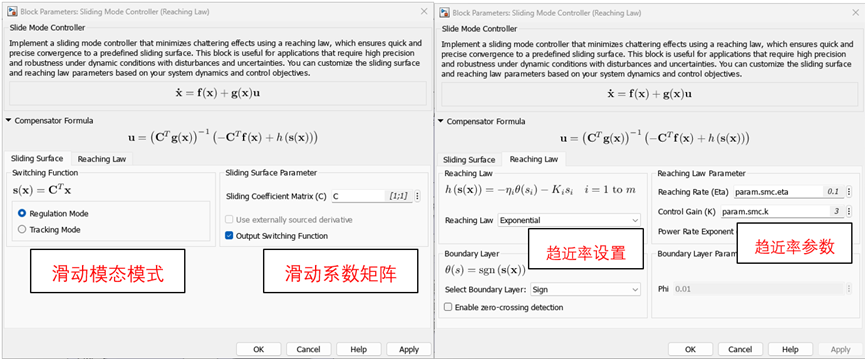
图5Simulink SMC 模块设置
我们希望控制器能在系统存在外部输入干扰的情况下,让质量滑块稳定在原点,建立如下 Simulink 模型来查看仿真结果。
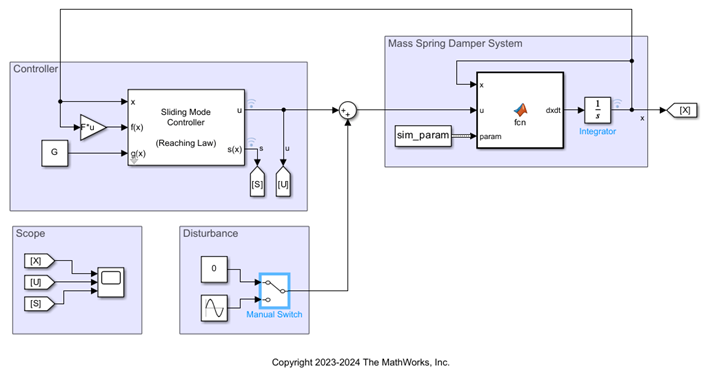
图6Simulink SMC闭环模型
在图5 的 SMC 模块设置中,除了我们已经介绍过的参数,还出现了一个参数叫做“Boundary Layer”,这就涉及到滑模控制的一大缺点-“颤振”。还是考虑图4所示的滑模面,滑模控制的理想情况是当系统状态到达滑模面时,不再离开滑模面,沿着其移动。但在实际物理系统中,“误差”不可避免地存在,所以实际上系统状态在到达滑模面时,并不“严格”沿着其移动,而会在其附近“来回晃动”(如图中蓝色折现所示)。
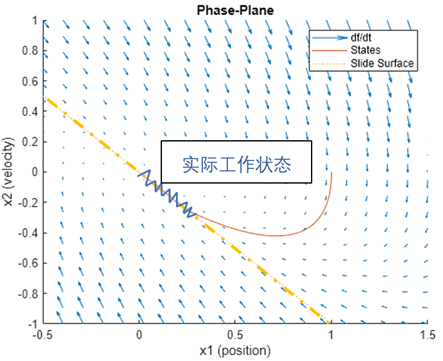
图7 滑模面实际工况示例
我们在一开始概述的时候讲到,滑模控制与常规控制的区别在于控制的不连续性,其在滑模面两边的控制输入完全不同,在滑模面附近晃动会使得系统的控制输入呈现“高频开关”的状态,从而导致“颤振”现象的发生。
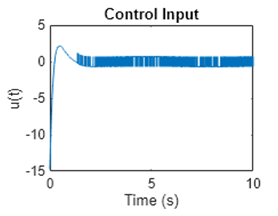
图8SMC控制输入“颤振”现象
为了防止这种现象的发生,我们需要设定一个合理的“边界”,当系统的状态没有偏离滑模面到边界值时,视为其仍然在滑模面上,不做控制输入的切换,实现一定程度上的“滞回”作用(如图中虚线所示)。
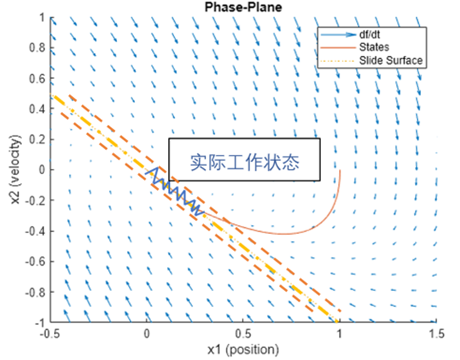
图9SMC 模块中Boundary Layer的设定意义
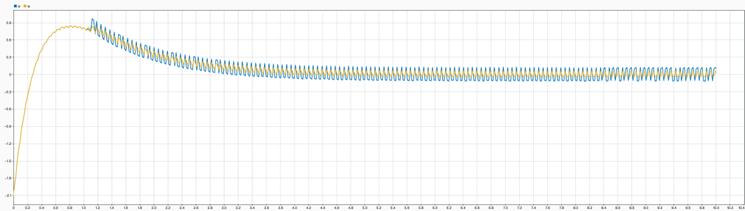
图10 不同Boundary Layer 参数下的输入颤振对比
典型案例分析之二变参数机械臂控制
现实世界中的真实物理系统当然远比上述的质量-弹簧-阻尼系统复杂得多,外部干扰对系统本身的影响也大得多。简单的被控对象可以帮我们充分理解滑模控制的原理以及优缺点,并帮助我们应用在更加贴近物理实际的场景当中。在 24b 的帮助文档中,还内置了另外一个更加复杂的 SMC 机械臂应用案例,SlidingMode Control Design for a Robotic Manipulator [3]。
示例中,我们考虑带有两个关节的机械臂,并且其本身的动态特性(状态方程中的矩阵参数)与标称值是有偏移的,当下图中机械臂状态矩阵的估计器(Estimator)无法准确估计真实的机械臂系统时,SMC暂展示出了良好的控制性能,能够应对系统中的未知干扰与不确定性。
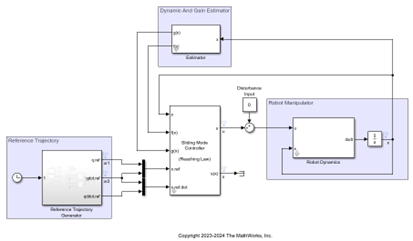
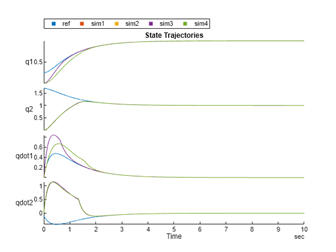
图11 机械臂滑模控制示例
因为篇幅的关系,此案例就不作详细介绍了,各位可以参阅帮助文档链接,在软件中打开模型进一步研究。
写在最后
MathWorks 在近些年来的版本中持续关注着广大用户对于非线性控制的需求,陆续添加了许多“即插即用”的控制算法模块(如前文提到的自控扰控制、模型参数自适应控制、极值搜索控制、模型预测控制等等),使得控制工程师们不必纠结于如何用代码实现相对成熟的控制理论本身,而是把精力更多地放在充分了解自身的被控物理对象特性,有理有据地调节控制算法中的参数,从而快速实现并基于自动代码生成无缝部署到嵌入式硬件中。
除了本文提到的滑模控制,在新版本中,MATLAB/Simulink 还发布了迭代学习控制(Iterative LearningControl, ILC)模块,帮助有需要的用户快速实现并部署该算法。 我们也乐于听到大家的心声,如果您有更多关于先进控制算法的使用需求和场景,不妨通过留言告诉我们,帮助 MATLAB/Simulink 持续提升!
-
matlab
+关注
关注
184文章
2970浏览量
230337 -
机器人
+关注
关注
211文章
28337浏览量
206857 -
Simulink
+关注
关注
22文章
533浏览量
62352 -
航空航天
+关注
关注
1文章
384浏览量
24269
原文标题:高效应对“外部干扰与非线性” - Simulink 滑模控制(SMC)更新探讨
文章出处:【微信号:MATLAB,微信公众号:MATLAB】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
PMSM在Simulink下的FOC滑模速度环仿真
IPMSM调速系统滑模变结构控制

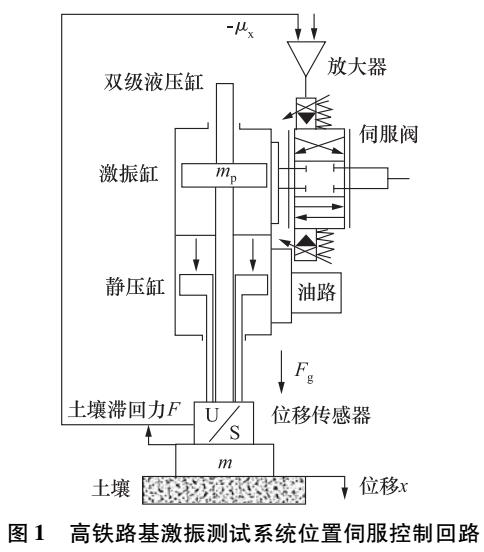
激振测试系统滑模控制特性分析




 Simulink滑模控制原理概述
Simulink滑模控制原理概述











评论