增量式pid参数调整公式及策略

PID算法是工程控制领域常用的一种算法，其有着技术成熟，不需要建立数学模型，参数整定灵活，适用性强，鲁棒性强，控制效果好等优点，得到了广泛的应用，其参数整定对控制效果影响极大，针对增量式的PID的参数整定方法在现有的文献中较少涉及。

PID分位置式PID和增量式PID两种，由于位置式PID控制的输出与整个过去的状态有关，用到了误差的累加值；而增量式PID的输出只与当前状态和前两状态的误差有关，因此位置式PID控制的累积误差相对更大，增量式PID输出的是控制量增量，如果微处理器出现故障，误动作影响较小，而执行机构本身有记忆功能，可仍保持原位，不会严重影响系统的工作，而位置式的输出直接对应对象的输出，对系统影响较大，因此实际中增量式PID应用更加广泛。

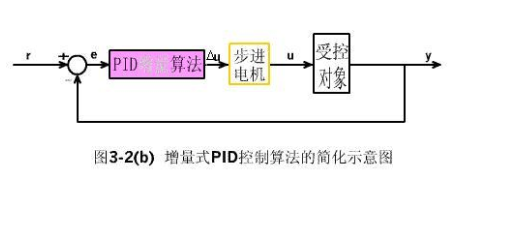
增量式PID控制

增量式PID控制，数字PID控制算法的一种基本形式，是通过对控制量的增量（本次控制量和上次控制量的差值）进行PID控制的一种控制算法。

增量式PID控制主要是通过求出增量，将原先的积分环节的累积作用进行了替换，避免积分环节占用大量计算性能和存储空间。

增量式PID控制的主要优点为：

①算式中不需要累加。控制增量Δu（k）的确定仅与最近3次的采样值有关，容易通过加权处理获得比较好的控制效果；

②计算机每次只输出控制增量，即对应执行机构位置的变化量，故机器发生故障时影响范围小、不会严重影响生产过程；

③手动—自动切换时冲击小。当控制从手动向自动切换时，可以作到无扰动切换。

由于增量式需要对控制量进行记忆，所以对于不带记忆装置的系统，只能使用位置式PID控制方式进行控制。

增量式pid参数调整公式

增量式PID控制根据位置式PID控制公式，写出n-1时刻的控制量：

设

得到

令 为积分系数； 为微分系数，可以将上式简化为

增量式PID控制算法

当执行机构需要的不是控制量的绝对值，而是控制量的增量（例如去驱动步进电动机）时，需要用PID的“增量算法”。

增量式PID控制算法可以通过（2-4）式推导出。由（2-4）可以得到控制器的第k-1个采样时刻的输出值为：

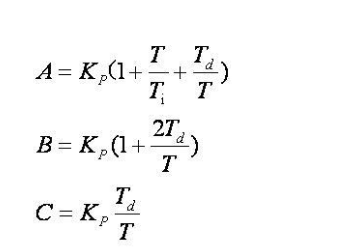
由（2-6）可以看出，如果计算机控制系统采用恒定的采样周期T，一旦确定A、B、C，只要使用前后三次测量的偏差值，就可以由（2-6）求出控制量。

增量式PID控制算法与位置式PID算法（2-4）相比，计算量小得多，因此在实际中得到广泛的应用。

位置式PID控制算法也可以通过增量式控制算法推出递推计算公式：

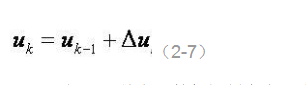
（2-7）就是目前在计算机控制中广泛应用的数字递推PID控制算法。

增量式PID控制算法C51程序

/*====================================================================================================

PID Function

The PID （比例、积分、微分） function is used in mainly

control applications. PIDCalc performs one iteration of the PID

algorithm.

While the PID function works， main is just a dummy program showing a typical usage.

=====================================================================================================*/

typedef struct PID

{

int SetPoint; //设定目标

Desired Value long SumError; //误差累计

double Proportion; //比例常数 Proportional Const

double Integral; //积分常数 Integral Const

double Derivative; //微分常数 Derivative Const

int LastError; //Error［-1］

int PrevError; //Error［-2］

} PID;

static PID sPID;

static PID *sptr = &sPID;

*=======================================================================

Initialize PID Structure PID参数初始化

=====================================================================================================*/

void IncPIDInit（void）

{

sptr-》SumError = 0;

sptr-》LastError = 0; //Error［-1］

sptr-》PrevError = 0; //Error［-2］

sptr-》Proportion = 0; //比例常数

Proportional Const sptr-》Integral = 0; //积分常数Integral Const

sptr-》Derivative = 0; //微分常数

Derivative Const sptr-》SetPoint = 0;

}

/*====================================================================================================

增量式PID计算部分

=====================================================================================================*/

int IncPIDCalc（int NextPoint）

{

register int iError， iIncpid; //当前误差

iError = sptr-》SetPoint - NextPoint; //增量计算

iIncpid = sptr-》Proportion * iError //E［k］项

- sptr-》Integral * sptr-》LastError //E［k－1］项

+ sptr-》Derivative * sptr-》PrevError; //E［k－2］项

//存储误差，用于下次计算

sptr-》PrevError = sptr-》LastError;

sptr-》LastError = iError;

//返回增量值

return（iIncpid）;

}

结合上述公式探讨PID的普遍控制规律和常用参数整定方法

（一）先来讨论PID三个参数的控制规律

1. 比例调节规律（Kp）：是按比例反应系统的偏差，系统一旦出现了偏差，比例调节立即产生调节作用用以减少偏差。

2. 积分调节规律（Ki）：实质上就是对偏差累积进行控制，直至偏差为零。使系统消除稳态误差，提高无差度。

3. 微分调节规律（Kd）：微分作用反映系统偏差信号的变化率，具有预见性，能预见偏差变化的趋势，因此能产生超前的控制作用，在偏差还没有形成之前，已被微分调节作用消除。

4. 比例积分微分控制规律PID：PID控制规律是一种较理想的控制规律，它在比例的基础上引入积分，可以消除余差，再加入微分作用，又能提高系统的稳定性。

（二）再来讨论PID参数整定的一般方法

1. 实验凑试法，整定步骤为“先比例，再积分，最后微分，这也是初接触PID的人常使用的。

2. 理论计算整定法。它主要是依据系统的数学模型，经过理论计算确定控制器参数。

3. 实验经验法，扩充临界比例度法，实验经验法调整PID参数的方法中较常用的是扩充临界比例度法，其最大的优点是，参数的整定不

依赖受控对象的数学模型，直接在现场整定、简单易行。

总之，对于PID的初用者，增量式的PID参数整定的时候，采用同位置式的比例Kp，积分Ki，微分Kd相同的系数，理解起来比较容易，整定自然就会符合以上所说的规律，可以达到预期的控制效果。