补码就是正数的原码的相反数的另一种编码方式。它能把字长内的正数,补足为全是0。
补码的意义:
现实生活中,我们有加法、减法、乘法和除法,但在计算机中只有一个加法器。换句话说,加法运算在计算机中可以直接完成,减法、乘法和除法运算最终也得转换为加法才能实现,说到这里,可以有些初学者会想,为什么计算机中不设计一个类似于“加法器”的“减法器”或者“乘法器”的部件,主要原因是在生活中看似一些很简单的东西要用电路来实现都很复杂、很困难的,再说如果用一个加法器可以实现其它运算,其它的“加法器”、“减法器”或者“乘法器”也就没有必要了,这样还能使电路的设计更简单。好了,现在我简要地说一下补码在计算机中的意义,计算机不能直接做减法,必须把相应的减法变成加法,才能进行计算。然而我们发现,一个数减去另外一个数,与一个数加上“另外一个数的补码”结果是一样的。这就是补码对于计算机的意义:将减法运算变成了加法运算。
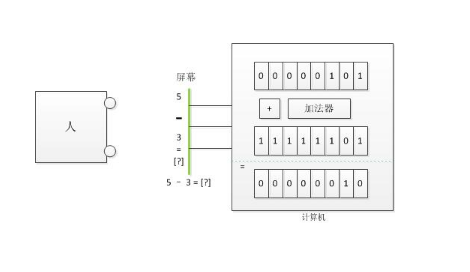
补码有什么用?
正数的补码,就是基本身
负数的补码,就是原码按位取反加1
符号位,就是最高位,最左面的第一位;其它位,就是剩下的7位
由于运算器进行加法是最快的,因此,使用补码是为了加快计算
码”和“数”是两个东西。
我们平时说出或写出某“数”,一般都是在十进制下,用10个不同的“码”(此处的“码”还和原码补码反码的概念不同)来表示。分别是0~9。超过9,也就是比最大的码还大的数,采用进位的方式来表示。于是有了“位”的概念。即个位,十位,百位等等。
表达负数的时候由于为了与算术和代数符号当中减号或作差相互兼容,就在该数前面加上减号。
这种对一个数的写法也可以被名门为一种编码方式。在这种编码方式下每个数都有一定的“位数”,即“长度”。在计算机当中规定一定的位数称作“字长”,比如4位,8位,16位,32位等等。只不过,计算机的物理存储数据是二进制方式。我们人类目前传统的还是比较喜欢用10进制方式。并且,我们人类一般不会在书写数字的时候遇到“字长”的概念。但是在念数字和记录数据的时候,有一点点东西跟字长相关。比如西方爱把数据分成三位一组三位一组的方式,觉得比较好记忆。比如12‘000读成十二千,我们中国人爱以“万”为字长,1’2000,读作一万二千。举这个例子表示字长的概念不是很恰当。因为对人而言这只是一种表达习惯。但是对机器而言,“字长”则是计算的长度单位。设计计算机进行最简单的加法运算,首先要考虑的就是加法器进行一次加法运算,位数是多长?加法器设计成多少位的加法器?等等。这就是计算机的字长。它和编码方式一起,构成了计算机进行计算的基础。
有了字长的概念才好说补码。
在十进制下也有补码的概念。插一句,谈到补码一定要先明确字长的长度。
补码是用来表示负数的一种编码方式。也是为了在计算机的核心加法器部分的设计避免减法操作,存储数据的时候避免存储负号。
举个例子,假如我们模拟一个字长为4位的十进制计算机。(假设有某种机制,可以在1位上有10种稳定的状态)
对两个数进行求和运算:1234 和 -1234
如果用原码,那么我们需要用一个1位的寄存器来存储和表示负号。假设就在4位的最左边的最高位前用1表示负号,0表示正号。
则,原码表示上面两个数:
0 1234
1 1234
然后计算机做求和,做加法的过程中。计算机发现,其中有一个数是负数,于是要切换为两个正数相减的模式来运算。这很不方便。
于是,补码被想出来了。
-1234和正1234相加不是等于0000吗?在4位的字长当中的数,和1234相加为0000的,是不是唯一的一个数哪?很明显8766和1234相加等于1‘0000,后4位是0000。
那么,8766就可以看着是-1234的一种编码表示方式,被称作“补码”。
所以,补码就是把数1234在一个字长内,补足为1’0000的数的编码方式。也就是一个正数的相反数,在计算机内的表达方式。
加上符号位,正数0‘1234的相反数的补码表示就是1’8766。
十进制里,-1234的反码就是1‘8765
所以,现在回到4位字长的2进制计算机里来看。补码和反码的构成方式是一样的。0’0001的相反数是-1。
补码表示1‘1111
反码表示1’1110
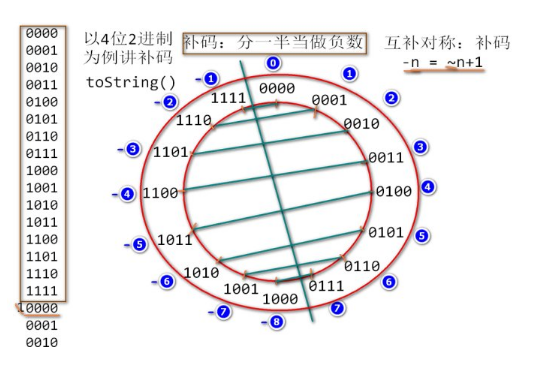
补码是谁发明的
谁发明的未知,但根据wikipedia上的说法,最初是冯诺依曼引入到计算机的。
很早以前,许多计算机的内部数值编码是用的反码,反码这玩意有缺点: 它的值域内有-0和+0,一个数与它的补数相加为-0,这给运算带来一些麻烦。
补码就没有这些问题,不但只有一个0,而且补码的加减乘法都可以化简为加法一种方式。 所以在计算机里补码对简化运算器有很大的作用。
补码的回顾以及补码发明的思路推演思考
补码与求补运算的定义
N个二进制位,M=N-1
通过一种编码映射。100.。.00 - 111.。.11 表示 (-2^M) - (-1) ; 000.。.00 - 011.。.11 表示 (0) - (2^M - 1)
对于编码A的求补 f(A) = (2^N)- A
原码转化成补码:
对于正数和零,原码即是补码
对于负数A,一般理解方法:
先做反码,然后编码意义上加1
求补运算的意义:
换言之,若要对一个数A求反,对那个数的补码A1做一次求补运算f(A1),所求的补码B1就是原来数A的相反数B的补码。
这里提供原码转化成补码另外一个理解方法
对于求负数A的补码
本质上,负数A的相反数B,B是正数,B的原码B1就是B的补码,A的补码就是f(B1)
---
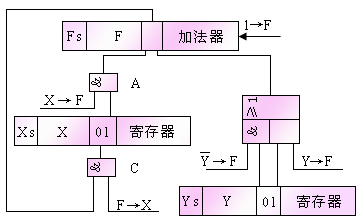
机器实现:
x-y = x-1-y+1 = (x-1) - y + 1
在补码的转码中,这里的x=2^N
这里的(x-1) - y即使对y进行反码操作,在ALU中可以N位同时刷新
至于N位整数+1,有一定的进位延时。
---
边界情况:
容易看到,我们对-2^N求反,仍然是-2^N
对2^N-1求反,则是-(2^N)-1
---
利用补码这种编码性质
f(y) = -y
x + y = x + y
x - y = x + f(y)
---
马后炮:事后猜测补码发明的思路, 从而看补码的优势
先看正码表示,设N=4, -1 = 1001; -2 = 1010, -1 》 -2, 但是 1001 《 1010,两种映射的编码的序性不一致
反码呢,-1=1110, -2 = 1101, Ok,序性正确了,
然而,这里有一个问题,就是正数与负数之间,有一个1的缝隙。-1=1110, 1=0001,从循环编码的角度,这两个编码相差3:1110-》1111-》0000-》0001。
因为正零和负零是两个数,导致两个数系的断裂。怎么办?让负数整体往正数靠拢,迈进一步(+1),负1没有了。
这就是求补的过程了。反码再加1。
我想,当初写出计算机的编码设计论文的大牛(好像是图灵还是什么的),当然有更深的考虑。但从序性和数系联系的角度,补码的发明是相当合理的。而这种合理性,我个人认为,正是其优点。
从机器实现的角度,并不算复杂,但相对反码的机器实现,还是多了+1的进位延时。
---
int与unsigned int的思考
顺便,我也整理一下这里的误区。
如果声明变量a为int,但是却当作unsigned int,如果正常累加超出范围,转化成unsigned int结果应该还是可信的。
不过算了,我们利用好转换和保证类型的一致,这些底层的问题我们确实还是当作透明为好。
-
补码
+关注
关注
0文章
14浏览量
7597
发布评论请先 登录
相关推荐
补码是什么 补码和原码的转化
补码加、减运算规则
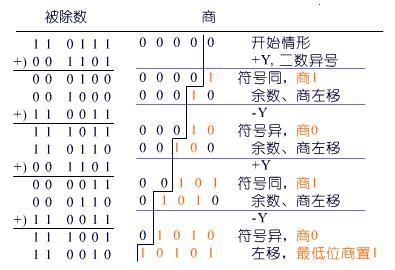
定点补码一位除法的实现方案




 补码是谁发明的_补码有什么用
补码是谁发明的_补码有什么用











评论