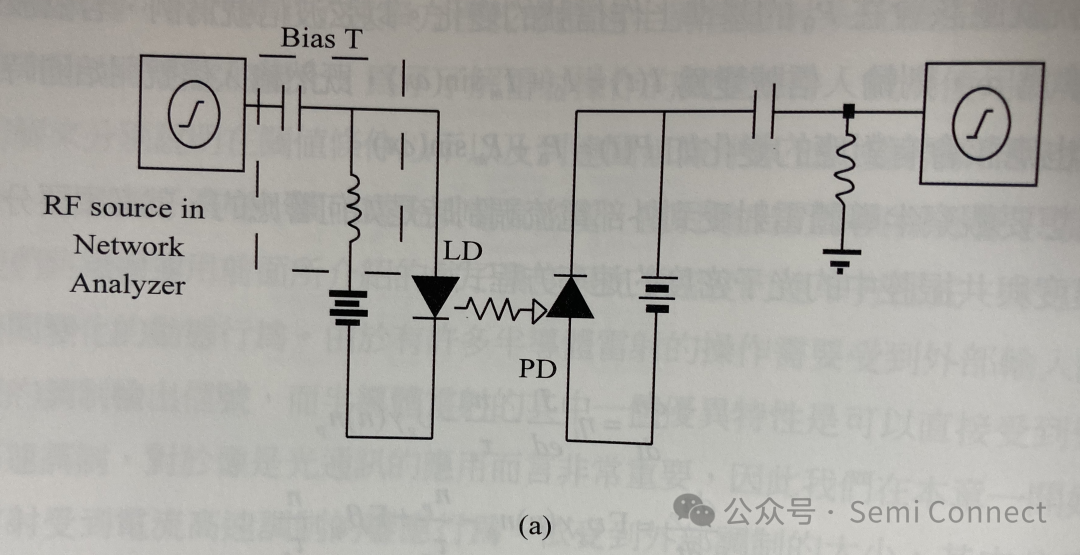
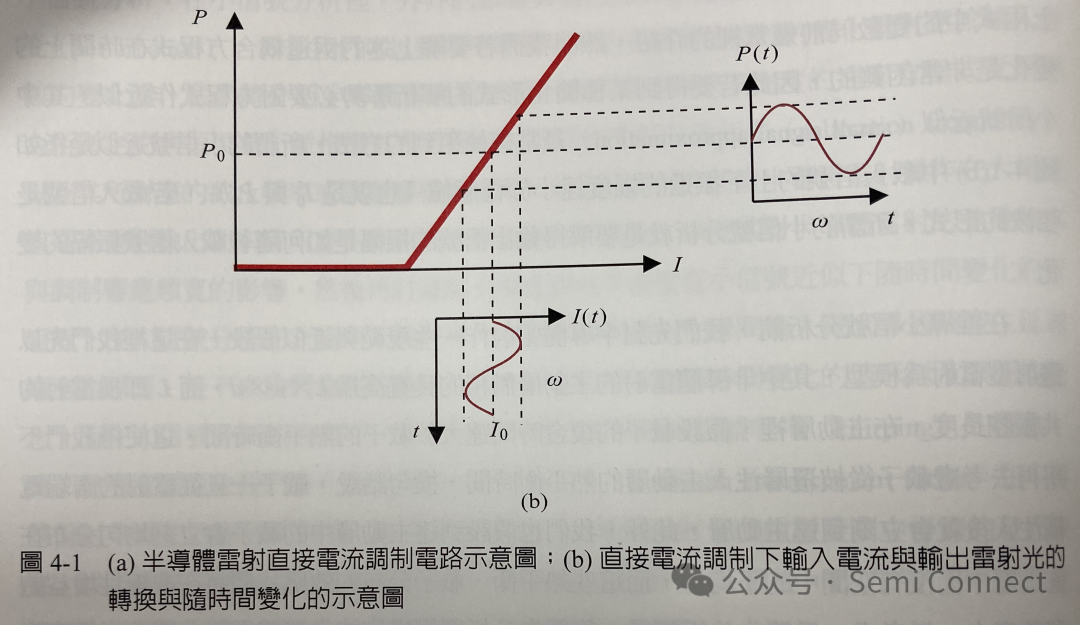
最常见的半导体雷射调制是如图4-1的直接电流调制,半导体雷射偏压操作在固定的电流值I0上,欲输入的信号从网络分析仪中产生经过Bias-T后加载到半导体雷射上,雷射的输出信号就应该会在P0的基准上作信号的变化。以弦波信号为例,若弦波的振幅为Im,振荡频率为w,则输入信号变为I(t)=I0+ImSin(wt),既然输入信号开始随时间变化,雷射光输出也应该会有对应的变化如P(t)=P0+pmsin(wt)。
当我们想要观察半导体雷射受到外部电流调制时是如何响应的,就必须要分析主动层中的载子浓度与共振腔中的光子密度的速率方程式:
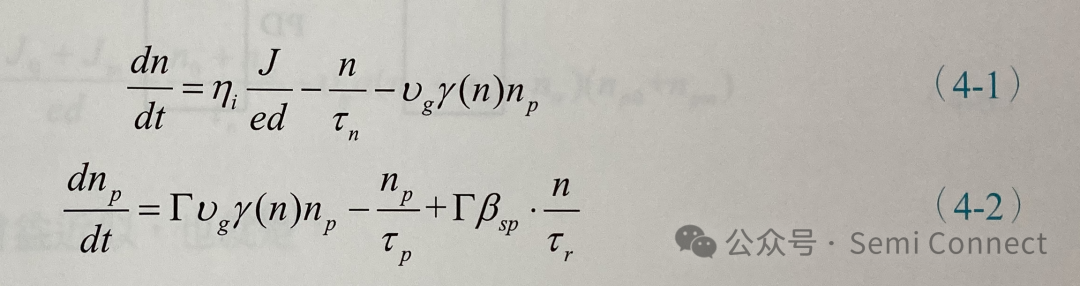
上两式中的变数同前几章里的介绍,然而我们若要解上述的两道耦合方程式在时间上的变化是非常困难的,因此若要得到某种简化形式的解析解势必要对方程式作近似,其中小信号近似(small signal approximation)是常被使用到的方法,所谓的小信号近似是指如图4-1(b)中载入信号的上下振荡的幅度远小于稳态值(也就是I0与P0),若载入信号是弦波的形式,所谓的小信号分析就是要解得输出信号的振幅是如何随着载入信号振幅的变化。
在推导小信号分析前,我们先对半导体雷射作一些规范与近似假设,在这里我们先以边射型雷射为模型,其中半导体雷射的主动层体积的长宽高为LxWxd,而L即为雷射的共振腔长度,在主动层里,假设载子的复合时间远大于载子的热平衡时间,这使得我们不用再去考虑载子从披覆层注入主动层的热平衡时间,换句话说,载子一旦从雷射的两端电极注入后就会立刻到达主动层,此外,我们也假设到达主动层中的载子会立刻均匀分布在主动层中而没有空间中的不均匀,而这些热平衡、载子分布的效应我们将在非线性增益饱和效应中一并考虑;为简化分析起见,我们先分析单模操作的半导体雷射,因此光子密度的速率方程式就只会有一道,此外,因为在边射型雷射中自发放射因子βsp太小我们可先忽略不考虑。
因此在小信号分析的情况下,我们可以定义电流密度、载子浓度与光子密度随时间的表示式:


我们假设Jo>Jm、n0>nm与np0>npm,其中下标0表示固定的稳态値,而下标m则表示小信号值。将上三式代入(4-1)式中并使用线性增益近似,即,我们可得:
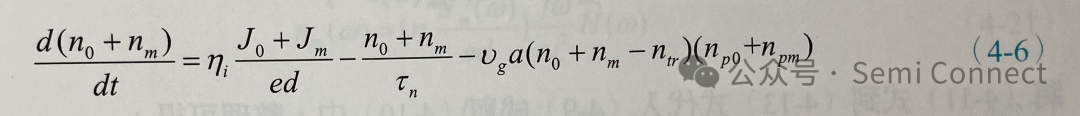
上式中我们使用了线性增益近似,也就是:
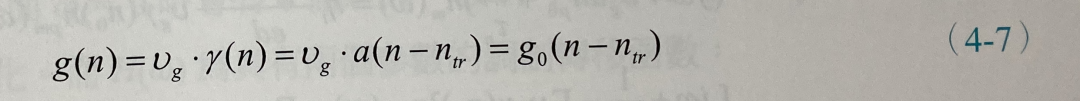
将(4-6)式展开,因为两个小信号相乘的项nm・npm太小可以忽略不计,并将稳态项以及小信号项分别放在一起,可得:
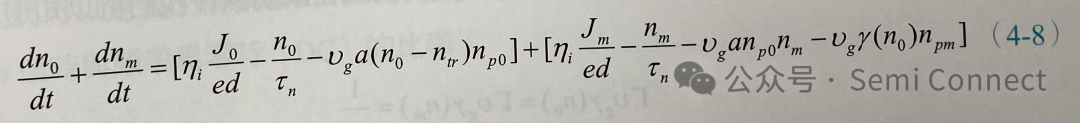
我们可以取出载子浓度小信号的变化为:
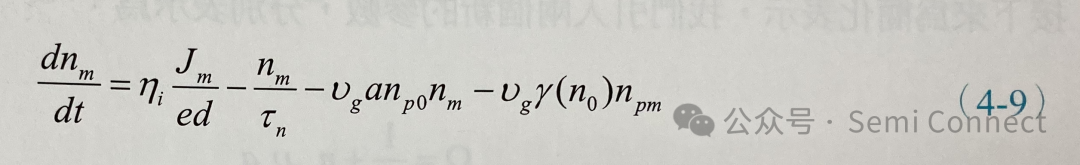
同样的,对于计算光子密度小信号的变化,我们可以将(4-3)式到(4-5)式代入(4-2)式中,展开之后将两个小信号相乘的项nm・npm=0,并将稳态项以及小信号项分放在一起,可得光子密度小信号的变化:
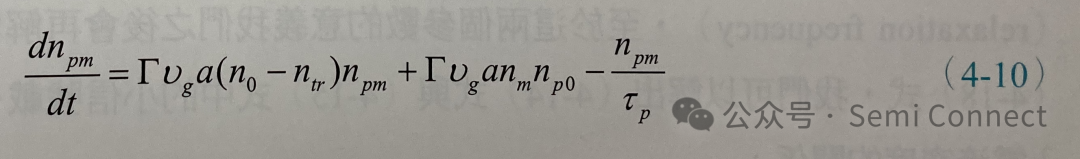
(4-9)式与(4-10)式即为载子浓度与光子密度的小信号速率方程式,我们可以发现,此二道方程式彼此之间又是互相耦合的。若小信号以弦波方式振荡,则:
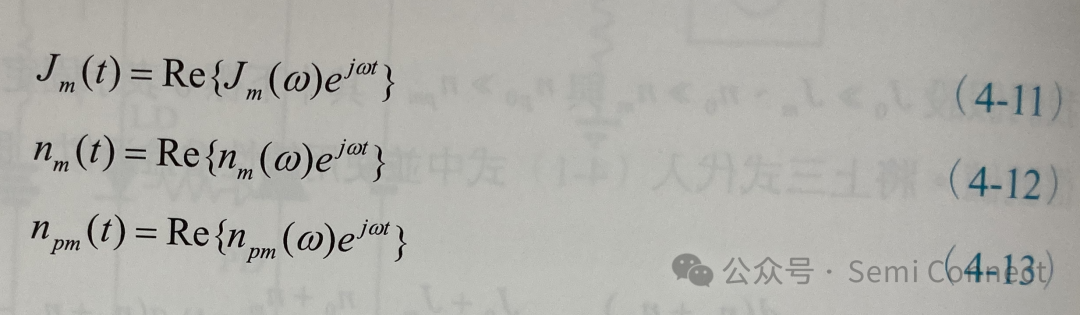
将(4-11)式到(4-13)式代入(4-9)式与(4-10)中,整理可得:
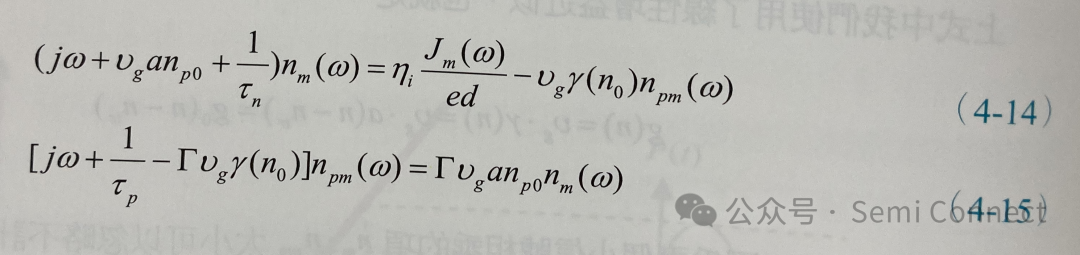
我们在前几章介绍过当雷射操作在阈值条件以上时,尽管输入电流改变,其载子浓度会被钳制在nth,因此nth即为载子浓度的稳态值n0,因此从阈值条件我们可以知道:

接下来为简化表示,我们引入两个新的参数,分别表示为:
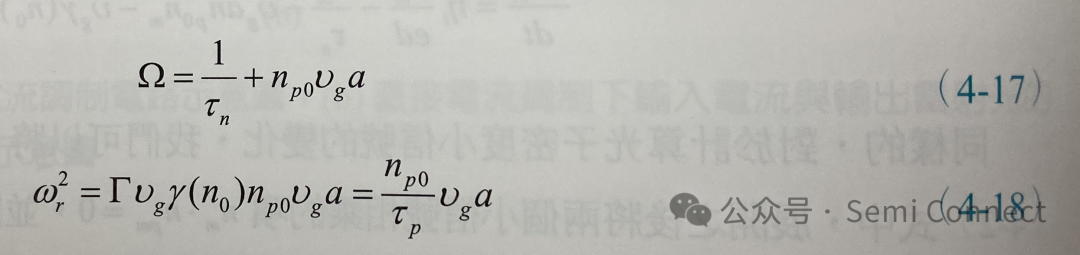
其中Ω被称之为阻尼常数(damping constant)或衰减率,而Wr则被称之为弛豫频率(relaxation frequency),至于这两个参数的意义我们之后会再解释。使用(4-16)式到(4-18)式,我们可以解出(4-14)式与(4-15)式中的小信号载子浓度与光子密度对输入电流密度的关系:
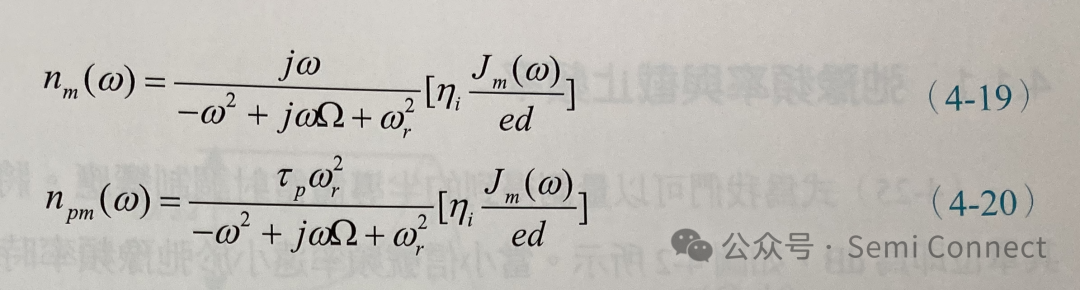
上式也可以整理成:
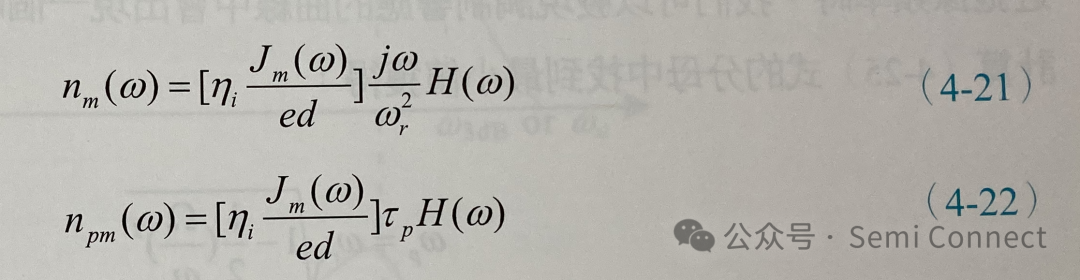
其中除了nm在复数平面w=0时会有0值之外,我们可以发现nm和npm主要都是随着H(w)的频率响应作变化。而H(w)为具有两个参数的调制转移函数:

我们可以定义小信号输出的调制响应(modulation response)为小信号光子密度在频率为w值时与频率为零时(DC)的比率:
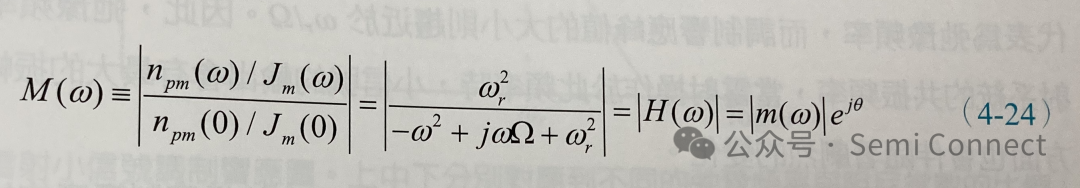
其中
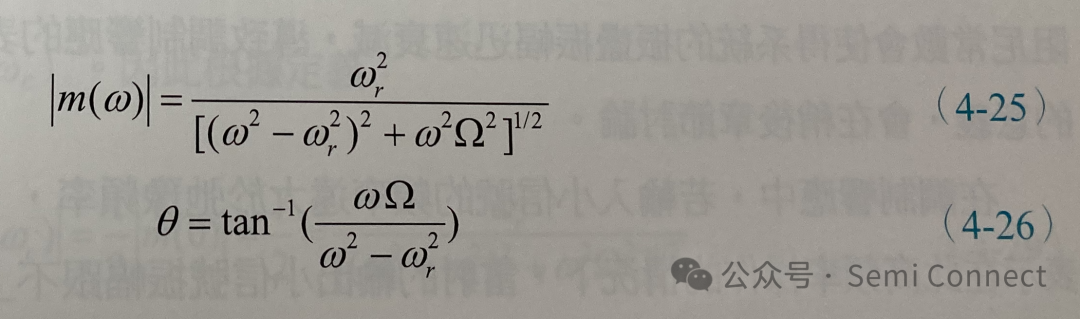
-
电流
+关注
关注
40文章
6979浏览量
133073 -
半导体
+关注
关注
335文章
27998浏览量
225416 -
小信号
+关注
关注
1文章
52浏览量
12251
原文标题:小信号响应
文章出处:【微信号:Semi Connect,微信公众号:Semi Connect】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐


如何为波特图设置频率响应分析仪
DCDC电源负载瞬态响应分析

Moku:Lab频率响应分析仪的应用指南
Moku:Lab频率响应分析仪在阻抗测量中的应用
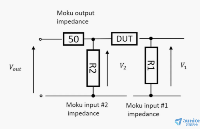
电源稳定性分析-Moku:Lab频率响应分析仪应用指南





 小信号响应分析
小信号响应分析










评论