汉明码原理介绍:
在计算机运行过程中,由于种种原因导致数据在存储过程中可能出现差错,为了能够及时发现错误并且将错误纠正,通常可以将原数据配成汉明编码。
汉明码具有一位纠错能力。
奇偶校验是一种添加一个奇偶位用来指示之前的数据中包含有奇数还是偶数个1的检验方式。如果在传输的过程中,有奇数个位发生了改变,那么这个错误将被检测出来(注意奇偶位本身也可能改变)。一般来说,如果数据中包含有奇数个1的话,则将奇偶位设定为1;反之,如果数据中有偶数个1的话,则将奇偶位设定为0。换句话说,原始数据和奇偶位组成的新数据中,将总共包含偶数个1.
奇偶校验并不总是有效,如果数据中有偶数个位发生变化,则奇偶位仍将是正确的,因此不能检测出错误。而且,即使奇偶校验检测出了错误,它也不能指出哪一位出现了错误,从而难以进行更正。数据必须整体丢弃并且重新传输。在一个噪音较大的媒介中,成功传输数据可能需要很长时间甚至不可能完成。虽然奇偶校验的效果不佳,但是由于他只需要一位额外的空间开销,因此这是开销最小的检测方式。并且,如果知道了发生错误的位,奇偶校验还可以恢复数据。
如果一条信息中包含更多用于纠错的位,且通过妥善安排这些纠错位使得不同的出错位产生不同的错误结果,那么我们就可以找出出错位了。在一个7位的信息中,单个数据位出错有7种可能,因此3个错误控制位就足以确定是否出错及哪一位出错了。
汉明编码方案通用算法
下列通用算法可以为任意位数字产生一个可以纠错一位的汉明码。
一、1开始给数字的数据位(从左向右)标上序号, 1,2,3,4,5.。。
二、将这些数据位的位置序号转换为二进制,1, 10, 11, 100, 101,等。
三、数据位的位置序号中所有为二的幂次方的位(编号1,2,4,8,等,即数据位位置序号的二进制表示中只有一个1)是校验位
四、有其它位置的数据位(数据位位置序号的二进制表示中至少2个是1)是数据位
五、每一位的数据包含在特定的两个或两个以上的校验位中,这些校验位取决于这些数据位的位置数值的二进制表示
1.校验位1覆盖了所有数据位位置序号的二进制表示倒数第一位是1的数据:1(校验位自身,这里都是二进制,下同),11,101,111,1001,等
2.校验位2覆盖了所有数据位位置序号的二进制表示倒数第二位是1的数据:10(校验位自身),11,110,111,1010,1011,等
3.校验位4覆盖了所有数据位位置序号的二进制表示倒数第三位是1的数据:100(校验位自身),101,110,111,1100,1101,1110,1111,等
4.校验位8覆盖了所有数据位位置序号的二进制表示倒数第四位是1的数据:1000(校验位自身),1001,1010,1011,1100,1101,1110,1111,等
5.简而言之,所有校验位覆盖了数据位置和该校验位位置的二进制与的值不为0的数。 采用奇校验还是偶校验都是可行的。偶校验从数学的角度看更简单一些,但在实践中并没有区别。
从编码形式上,我们可以发现汉明码是一个校验很严谨的编码方式。在这个例子中,通过对4个数据位的3个位的3次组合检测来达到具体码位的校验与修正目的(不过只允许一个位出错,两个出错就无法检查出来了,这从下面的纠错例子中就能体现出来)。在校验时则把每个汉明码与各自对应的数据位值相加,如果结果为偶数(纠错代码为0)就是正确,如果为奇数(纠错代码为1)则说明当前汉明码所对应的三个数据位中有错误,此时再通过其他两个汉明码各自的运算来确定具体是哪个位出了问题。
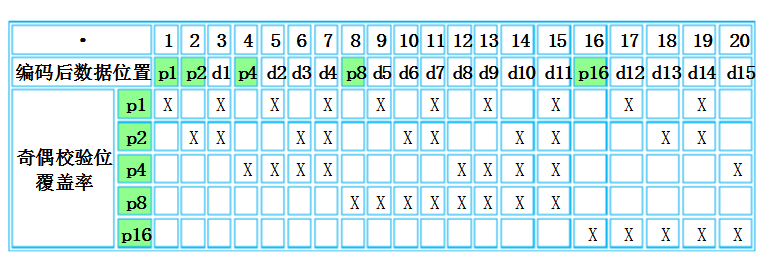
观察上表可发现一个比较直观的规律:第i个检验位是第2i-1位,从该位开始,检验2i-1位,跳过2i-1位……依次类推。例如上表中第3个检验位p4从第23-1=4位开始,检验4、5、6、7共4位,然后跳过8、9、10、11共4位,再检验12、13、14、15共4位……
汉明码的编码规则如下:
在新的编码的2^(k - 1)( k 》= 0)位上填入0(即校验位)
把新的编码的其余位把源码按原顺序填入
校验位的编码方式为:第k位校验码从则从新的编码的第2^(k - 1)位开始,每计算2^(k - 1)位的异或,跳2^(k - 1)位,再计算下一组2^(k - 1)位的异或,填入2^(k - 1)位,比如:
第1位校验码位于新的编码的第1位(2 ^(1-1) == 1)(汉明码从1位开始),计算1,3,5,7,9,11,13,15,。。。位的异或,填入新的编码的第1位。
第2位校验码位于新的编码的第2位(2 ^(2-1) == 2),计算2,3,6,7,10,11,14,15,。。。位的异或,填入新的编码的第2位。
第3位校验码位于新的编码的第4位(2 ^(3-1) == 4),计算4,5,6,7,12,13,14,15,20,21,22,23,。。。位的异或,填入新的编码的第4位。
第4位校验码位于新的编码的第8位(2 ^(4-1) == 8),计算8-15,24-31,40-47,。。。位的异或,填入新的编码的第8位。
第5位校验码位于新的编码的第16位(2 ^(5-1) == 16),计算16-31,48-63,80-95,。。。位的异或,填入新的编码的第16位。
在数学方面,汉明码是一种二元线性码。对于每一个整数m》2,存在一个编码,带有m个奇偶校验位2m- m-1个数据位。
汉明码的生成和检验
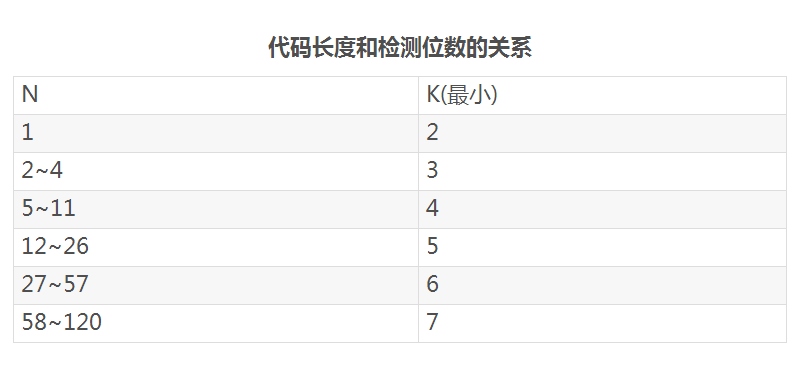
设将要进行检测的二进制代码为n位,为使其具有纠错能力,需要再加上k位的检测位,组成n+k位的代码。那么,新增加的检测位数k应满足:
2k≥n+k+1或2k-1≥n+k
当k的位数确定后,便可根据承担的检测任务设定他们在传送代码中的位置和他们的取值。首先,将所要检测的代码分为Pn组,分多少个组,我们通过k的值来确定。下面我用一个例子来说明。
假设将要进行检测的二进制代码为0101,位数n=4,根据公式2k≥n+k+1可以得出k的值是3,所以最终形成的汉明码应为n+k=7位。
所以分组分为P1、P2、P4。原因则是第一组是20、第二组则是21 、同理第三组则是22 、依次列推分组应按照2k-1。同时以后根据分组产生的数插入的位置也是按照此规律插入,比如第一组插入20、即第1位,第二组插入21 、即第2位,以此类推。那么组分好了,他们每一组中包含的位则是:
p1包含(1,3,5,7,9,11,。。。位)
p2包含(2,3,6,7,10,11,14,15,。。。位)
p3包含(4,5,6,7,12,13,14,15,。。。位)
每一组中包含的数又是如何确定的呢?我们来看下面这个表格

将编号转成二进制从右向左,如果第一位是1,例如编号是1,3,5,7.。。。的就分入第一组,如果第二位是1的,例如编号2,3,6,7,10.。。的就分入第二组,以此类推将所有的编号分入相应的组中。下面我么来看例子0101是如何产生汉明码的(采用配偶原则),
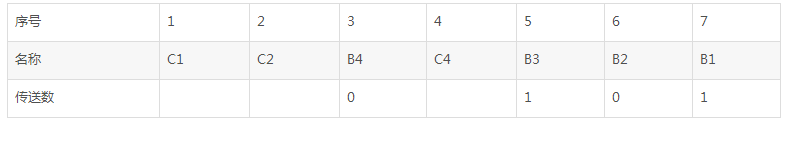
其中C1、C2、C4是我们插入的检测位
如果按照配偶原则来配置汉明码,则C1应使1 3 5 7位中“1”的个数为偶数;C2应使2 3 6 7位中“1”的个数为偶数;C4应使4 5 6 7位中“1”的个数为偶数。
按照上面我所说的则:
C1=③位+⑤位+⑦位,即C1=B4+B3+B1=0+1+1=0
C2=③位+⑥位+⑦位,即C2=B4+B2+B1=0+0+1=1
C4=⑤位+⑥位+⑦位,即C4=B3+B2+B1=1+0+1=0
所以0101的汉明码应为C1C2B4C4B3B2B1,即0100101
汉明码还存在配奇原则,下面来讲一讲配奇原则。按照配奇原则配置1100101的汉明码。
根据1100101可知n=7。根据公式我们可以求出需要添加k=4位检测位,详细情况如下表。

按配奇原则配置,则
C1=③位+⑤位+⑦位+⑨位+11位+1=1+1+0+1+1+1=1
C2=③位+⑥位+⑦位+10位+11位+1=1
C4=⑤位+⑥位+⑦位+1=0
C8=⑨位+10位+11位+1=1
所以按配奇原则新配置的汉明码为11101001101
汉明码校验错误实例
我们以上面的编码为例,假设我们现在收到的编码为001101001,我们可以发现汉明码的第8位与原来的汉明码001101011不同,那我们怎么找出这个第8位的错误编码呢?
算法很简单,我们只要在算汉明码校验位的算法的上再算一遍,就得到了汉明码的校验方法,比如计算001101001对应的2^k位。
1,3,5,7,9进行异或,得到0
2,3,6,7进行异或,得到0
4,5,6,7进行异或,得到0
8,9进行异或,得到1
我们把上述结果反着排列,得到1000,即十进制的8,根据汉明码的校验规则,编码出错的地方即在第8位,我们把第8位的0换成1,即可得原来的编码001101011。
上述的例子是出现在2^k的校验位上的,如果出现在非2^k位上,得到的结果也是一样的,比如:
假设收到的编码为001100011,即第6位出了错误,我们根据规则
1,3,5,7,9进行异或,得到0
2,3,6,7进行异或,得到1
4,5,6,7进行异或,得到1
8,9进行异或,得到0
我们把上述结果反着排列,得到0110,即十进制的6,根据汉明码的校验规则,编码出错的地方即在第6位,我们把第6位的0换成1,即可得原来的编码001101011。
汉明码的编码和校验的C++实现
通过原理,我们可以很简单地实现汉明码的编码和校验代码
auto cal(size_t sz)-》decltype(auto)
{
decltype(sz) k = 0;
decltype(sz) cur = 1;
while (cur - 1 《 sz + k )
{
cur 《《= 1;
k++;
}
return k;
}
bool encode(const string &s, string &d)
{
d.clear();
auto k = cal(s.size());
d.resize(s.size() + k);
for (decltype(d.size()) i = 0, j = 0, p = 0; i!= d.size();i++)
解码与校验:
auto antiCal(size_t sz)-》decltype(auto)
{
decltype(sz) k = 0;
decltype(sz) cur = 1;
while (cur 《 sz)
{
cur 《《= 1;
k++;
}
return k;
}
auto decode(string &s, string &d)-》decltype(auto)
{
s.clear();
auto k = antiCal(d.size());
s.resize(d.size() - k);
decltype(d.size()) sum = 0;
for (decltype(k) p = 0;p != k;p++)
{
int pAnti = 0;
decltype(k) index = 1 《《 p;
for (decltype(d.size()) i = index - 1;i 《 d.size(); i+=index)
{
for (auto j = 0; j 《 index && i 《 d.size(); i++, j++)
pAnti ^= d[i] - ‘0’;
}
sum += pAnti 《《 p;
}
if (sum != 0)
d[sum - 1] = (1- (int)(d[sum - 1] - ‘0’)) + ‘0’;
for (decltype(d.size()) i = 0, p = 0,j = 0; i != d.size(); i++)
{
if ((i + 1) == (1 《《 p) && p 《 k)
p++;
else
s[j++] = d[i];
}
return sum;
}
{
if ((i + 1) == pow(2,p) && p 《 k)
{
d[i] = ‘0’;
p++;
}
else if (s[j] == ‘0’ || s[j] == ‘1’)
d[i] = s[j++];
else
return false;
}
for (auto i = 0; i != k;i++)
{
int count = 0 ,index = 1 《《 i;
for (auto j = index - 1; j 《 d.size() ;j += index)
for (auto k = 0; k!= index && j 《 d.size(); k++, j++)
count ^= d[j] - ‘0’;
d[index - 1] = ‘0’ + count;
}
return true;
}
测试样例:
int main()
{
string source, dest;
while (cin 》》 source)
{
if (encode(source,dest))
{
cout 《《 “Source: ” 《《source 《《 endl;
cout 《《 “Dest: ” 《《 dest 《《 endl;
}
size_t index;
cout 《《 “----input error index : ”;
cin 》》 index;
auto k = dest.size();
if (index != 0 && index 《= dest.size())
dest[index - 1] = (1 - (int)(dest[index - 1] - ‘0’)) + ‘0’;
cout 《《 “Code ” 《《 dest 《《endl;
auto ret = decode(source,dest);
if (ret == 0)
{
cout 《《 “Source: ” 《《source 《《 endl;
cout 《《 “Dest: ” 《《dest 《《 endl;
}
else
{
cout 《《 “Error index ”《《 ret 《《 endl;
cout 《《 “Corret source: ” 《《source 《《 endl;
cout 《《 “Corret dest: ” 《《dest 《《 endl;
}
cout 《《 endl;
}
return 0;
}
Source: 10101
Dest: 001101011
----input error index : 8
Code 001101001
Error index 8
Corret source: 10101
Corret dest: 001101011
Source: 1001010101010101010111111001101
Dest: 1111001101010100101010101111110101101
----input error index : 20
Code 1111001101010100101110101111110101101
Error index 20
Corret source: 1001010101010101010111111001101
Corret dest: 1111001101010100101010101111110101101
Source: 1
Dest: 111
----input error index : 0
Code 111
Source: 1
Dest: 111
-
汉明码
+关注
关注
0文章
8浏览量
8098
发布评论请先 登录
相关推荐
基于FPGA的汉明码译码器如何对码元数据添加噪声干扰?
【原创】基于FPGA的汉明码编码解码设计
提高汉明码对突发干扰的纠错能力
一种基于汉明码和湿纸码的隐写算法
基于FPGA的检纠错逻辑算法的实现

汉明码计算及其纠错原理详解
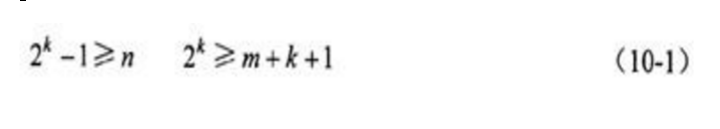
汉明码纠错的基本原理及优化解决方案





 汉明码原理和校验及实现
汉明码原理和校验及实现











评论