为要了解半导体雷射的大信号响应,我们先针对单模雷射的速率方程式求解,我们将使用线性增益近似以及考虑到增益抑制因子,而将载子浓度与光子密度对时间的变化方程式如下所列:
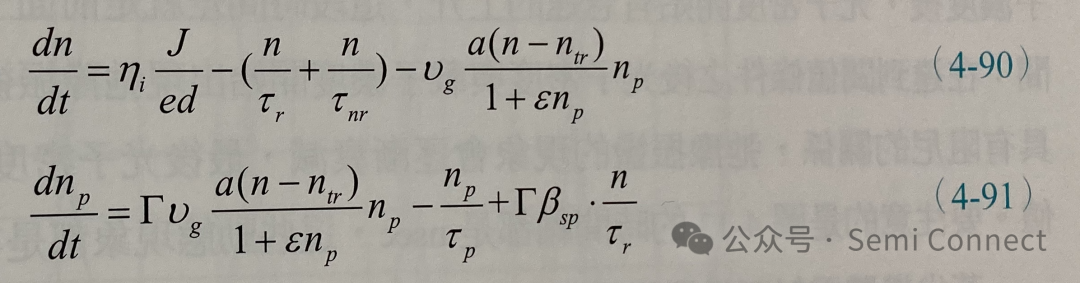
接下来要设定雷射的起始条件,也就是载子浓度与光子密度的值,并设定所计算的时间长度,从起始条件开始,每增加一小段的时间△t,再计算一次载子浓度与光子密度的值,直到我们设定的时间长度为止,其中迭代演算的数值方法可以用简单的Euler法或是Runge Kutta法等都可以用来数值计算(4-90)式与(4-91)式的耦合常微分方程式。关于Euler法或是Runge Kutta法的推导,我们不在这里介绍,有兴趣的读者可以参阅一般的数值方法教科书,或是直接使用套装的数学软体,如Matlab已经发展出简单使用的指令,可以快速套用。
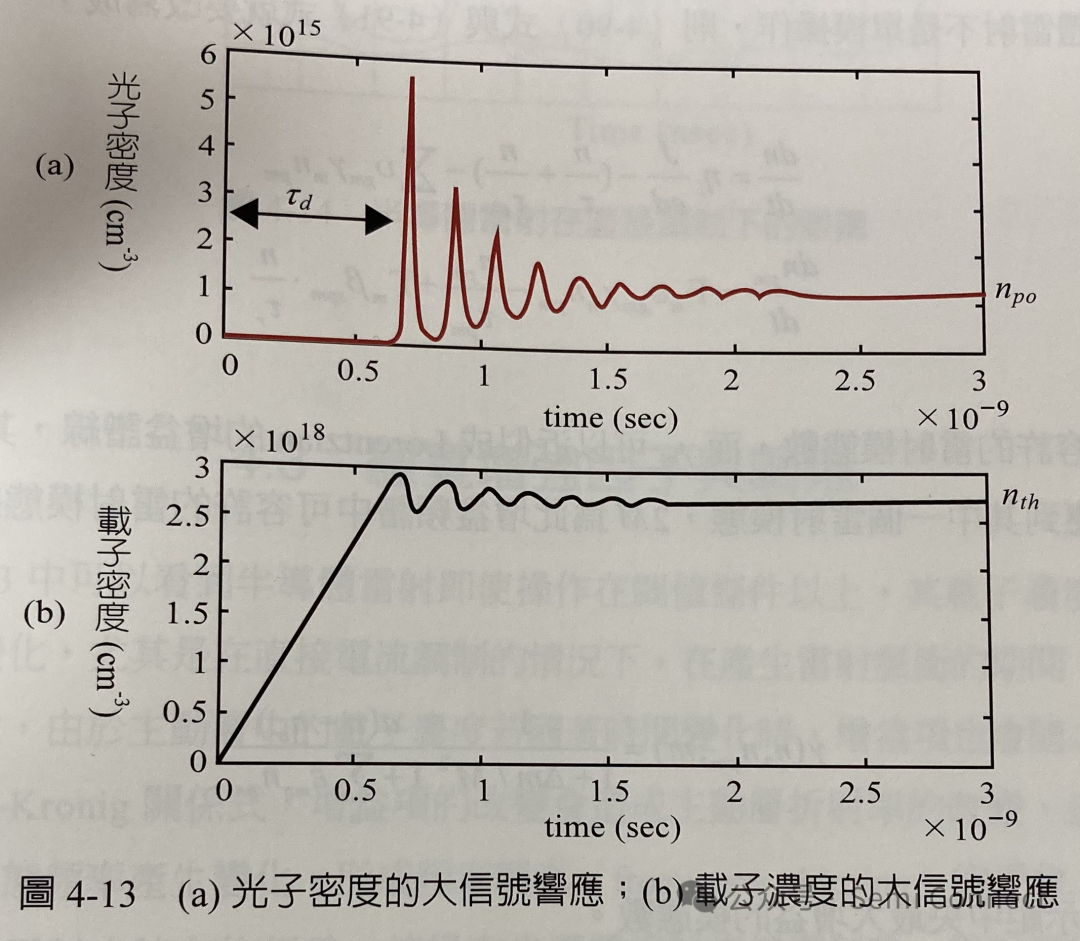
图4-13为使用Runge Kutta法所解的载子浓度与光子密度的大信号响应,其中输入电流从t=0开始以步阶的方式从0增加到阈值电流以上,我们可以看到载子浓度即随之增加,但是此时因为还未达到阈值载子浓度,因此光子密度为0,直到载子浓度到达阈值载子浓度后,光子密度开始有急速的上升,这段时间差就是前面一小节所介绍的导通延迟时间;在达到阈值条件之后光子密度与载子浓度开始出现弛豫振荡的现象,但是因为系统中具有阻尼的关系,弛豫振荡的现象会逐渐衰减,最后光子密度与载子浓度将会达到稳态值。要注意的是图4-13的时间轴都是nsec,这些动态现象都是在很短的时间内发生的。
若半导体雷射不是单模操作,则(4-90)式与(4-91)式就要改写成:
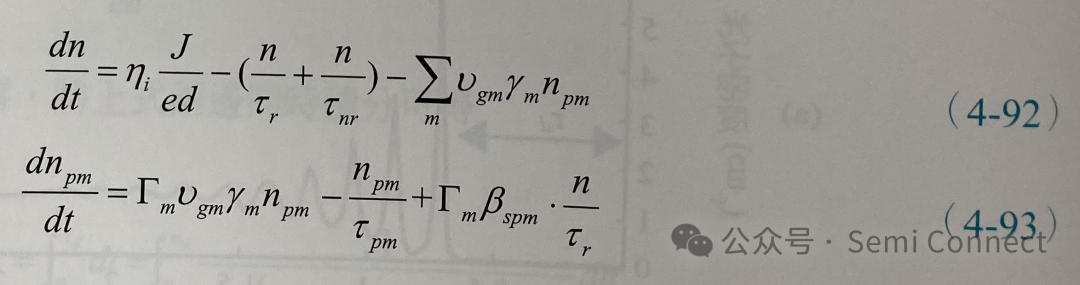
其中m为可容许的雷射模态数,而ym可以近似成Lorentzian的增盆谱线,其中增盆频谱的最大值对应到其中一个雷射模态,2M为此增益频谱中可容许的雷射模态总数,因此y可以表示为:
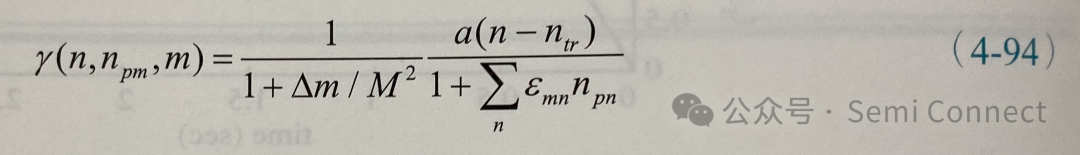
其中△m是表示距中央最大增益的模态数。
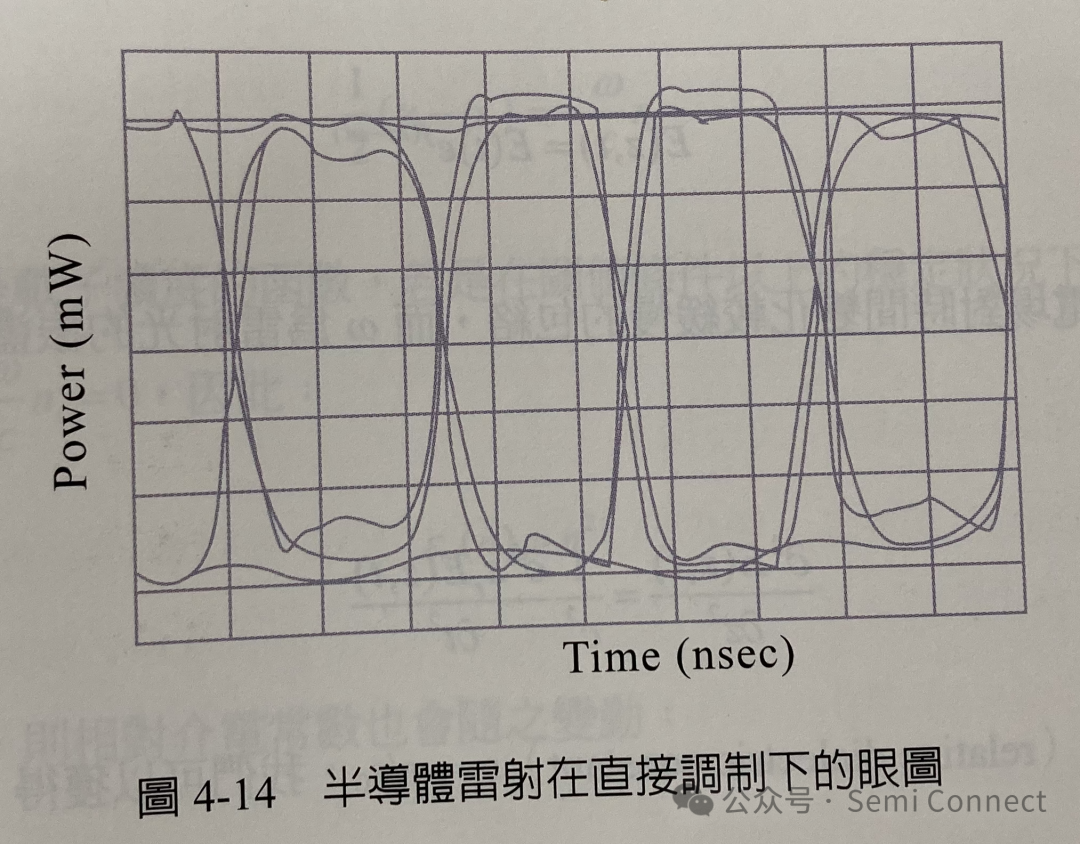
半导体雷射应用在数位光纤通讯系统中,通常要产生大信号的快速数位脉冲,前面所提到的导通延迟时间以及弛豫振荡都会使得雷射光输出的数位脉冲变形,而使得位元错误率(bit-error-rate)增加,我们通常会使用眼图(eye diagram)来评估半导体雷射在高速调制下的表现,由伪随机二进位序列产生器(pseudo-random binary sequence(PRBS)generator)产生出高速信号驱动雷射二极体,然后在示波器中叠加这些信号,如图4-14所示,我们可以看到雷射光的信号在时间中抖动(jitter)的动态行为,因此影响信号图形的行为都可以在眼图中被观察到,一般我们会定义在特定调制速度下,眼图中央干净的部分开口的大小,以判定其信号是否合乎此调制速度下的传输规范。
-
半导体
+关注
关注
334文章
27654浏览量
221314 -
雷射
+关注
关注
0文章
23浏览量
10257 -
大信号
+关注
关注
0文章
9浏览量
7526
原文标题:大信号调制之数值解
文章出处:【微信号:Semi Connect,微信公众号:Semi Connect】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐





 大信号调制之数值解
大信号调制之数值解











评论