FPGA频率测量的三种方法

1、FPGA频率测量？

频率测量在电子设计和测量领域中经常用到，因此对频率测量方法的研究在实际工程应用中具有重要意义。

通常的频率测量方法有三种：直接测量法，间接测量法，等精度测量法。

2、直接测量法

2.1、方法

直接测量法也叫频率测量法，即在固定在时间t内对被测信号的脉冲数进行计数，然后求出单位时间内的脉冲数，即为被测信号的频率。

下图中的信号分别为：

sys_clk：系统的基准时钟

gate：根据基准时钟生成的闸门信号，用于生成一个固定的时间（例如1s，方便计算）

clk_fx：被测信号

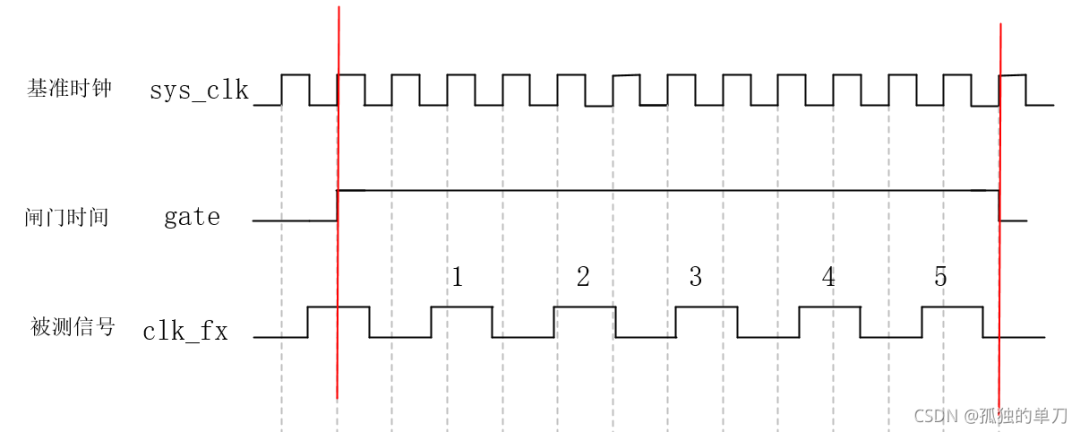
gate是在基准时钟下生成的固定时间信号，它持续的时间 Tg = sys_clk 计数个数N（可设置）；在gate持续为高的时间内，可使用被测信号clk_fx对其进行计数，计数个数为cnt（图中为5），则cnt个被测信号的周期即为gate时长。

此种方法的本质是：同样的时间内分别使用两种时钟计时，则有 Tg = Tfx---- Tsys_clk 计数个数N = Tclk_fx cnt，公式变换后：clk_fx = cnt sys_clk / 计数个数N （其中clk_fx为待测信号频率，sys_clk为基准时钟频率）

2.2、误差分析

从图可以看出，在gate为高电平期间，被测信号实际上差不多有六个周期被囊括在内，但是因为被测信号是相对与系统的异步信号，相位不同，第一个周期无法被采样，所以实际采样为5，这样造成的误差为一个被测信号周期。可以预见，这种测量方法带来的测量误差即为一个被测信号周期。

那么理论上测得的准确频率：clk_fxe = cnt sys_clk / 计数个数N----理论上cnt无误差

实际上测量的频率值：clk_fx= cnt±1 sys_clk / 计数个数N----cnt会存在一个周期的测量误差

测量误差 = |（clk_fxe -clk_fx）/clk_fxe | 100% = 1 / cnt 100%

所以测得的cnt越大，那么测出来的误差值就小，而cnt越大则代表被测信号的频率越高，所以可以推断该种测量方法适合测量高频信号；此外，选择的闸门时间越长则被测信号的个数越多，同样测量就越精确，但是增大闸门时间又会带来测量时间过长的问题，需要依据具体需求进行取舍。

2.3、Verilog代码

Verilog源码如下：

闸门时间设定为0.5s，非闸门时间也0.5s，则每1秒更新一次测量数据

使用计数器生成闸门时间，闸门时间取反得到非闸门时间

在闸门时间对被测信号计数

在非闸门时间更新测量数据

使用parameter定义参数，方便调用修改

//直接测量法(高频)
modulecymometer_direct(
input sys_clk,//基准时钟，设计为50M(可更改)
input sys_rst_n,//复位信号，低电平有效
input clk_fx,//待测信号
output reg [31:0]fre//测量结果
);

parameterTIME_SYS  = 20;//系统时钟周期：20ns--频率=50MHz
parameterTIME_GATE = 500_000_000;//500ms闸门设置的时间，单位：ns
localparamN = TIME_GATE /TIME_SYS;//生成闸门需要计数的个数

reg gate;//闸门
reg [31:0] cnt_gate;//用于生成闸门的计数器
reg [31:0] cnt_fx;//闸门时间内对被测信号计数

wiregate_n;//闸门取反，用于在非闸门时输出测得的频率值

assigngate_n = ~gate;//闸门取反，用于在非闸门时输出测得的频率值

//分频计数器，闸门时间设定为1ms，则每2ms测量一次
always @(posedge sys_clk or negedge sys_rst_n)begin
if(!sys_rst_n)begin
cnt_gate <=0;
gate <=0;
end
else begin
if(cnt_gate == N-1)begin
cnt_gate <= 0;
gate <= ~gate;
end
else
cnt_gate<=cnt_gate+1;
end
end 
 
//闸门时间内对被测信号计数
always @(posedge clk_fx or negedge sys_rst_n)begin
if(!sys_rst_n)
cnt_fx <= 0;
else if(gate)
cnt_fx <= cnt_fx + 1;
else
cnt_fx <= 0;
end

//在非闸门时输出测得的频率值
always @(posedge gate_n or negedge sys_rst_n)begin
if(!sys_rst_n)
fre <= 0;
else 
//TIME_GATE/cnt_fx=规定时间/被测信号个数=被测信号周期，取倒数即为频率
fre <= 1000_000_000/TIME_GATE * cnt_fx;
end

endmodule

2.4、仿真分析

Testbench：

设计被测信号周期为489*2=978ns，则其理论频率为1/978ns=1022494.88Hz；

`timescale 1ns/1ns//时间单位/精度

//------------<模块及端口声明>----------------------------------------
module tb_cymometer_direct();

reg sys_clk;
reg         sys_rst_n;
reg         clk_fx;

wire [31:0] fre;

// defparam cymometer_direct_inst.TIME_GATE = 500_000;          //地址位宽

//------------<例化被测试模块>----------------------------------------
cymometer_directcymometer_direct_inst(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx),

.fre       (fre)
);

//------------<设置初始测试条件>----------------------------------------
initial begin
sys_clk = 1'b0;//初始时钟为0
sys_rst_n <= 1'b0;//初始复位
clk_fx<= 1'b0;
#5//5个时钟周期后
sys_rst_n <= 1'b1;//拉高复位，系统进入工作状态
// #2500_000
// forever#2560 clk_fx = ~clk_fx;
end
//------------<设置时钟>----------------------------------------------
always #10 sys_clk = ~sys_clk;//系统时钟周期20ns
always #489 clk_fx = ~clk_fx;//被测信号周期489*2ns = 978ns

endmodule

仿真如下图：

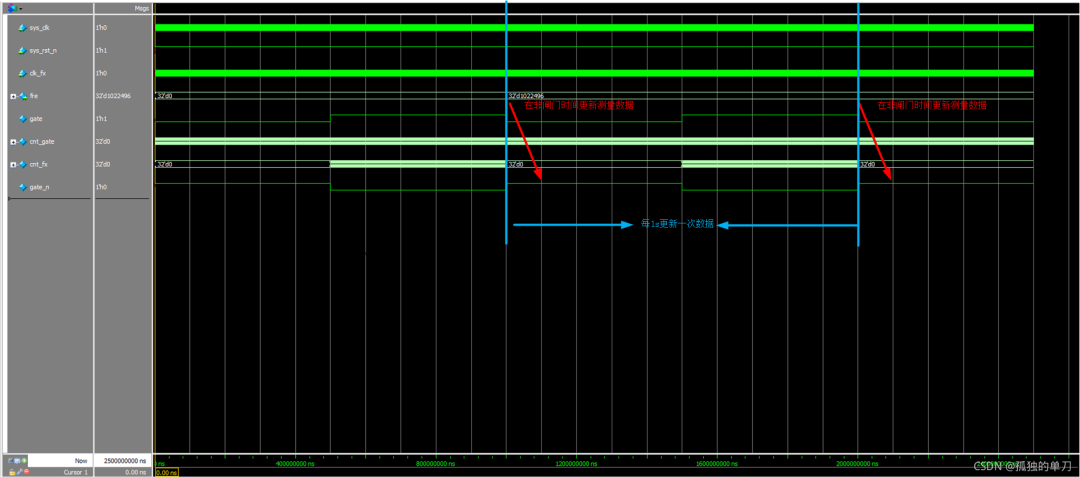
上图在闸门时间内测得的被测信号个数cnt_fx为511248，测得被测信号频率为1022496Hz；理论频率=1/978ns=1022494.88Hz（MHz级别）。

可以看出这个测量结果还是比较准确的。因为闸门时间够长，且被测信号自身频率就比较高（约1Mhz）。

接下来更改一下Testbench，比较一下闸门时间对被测信号的影响以及被测信号自身频率高低对测量的影响：

第1个模块：被测信号频率为1022494.88Hz（MHz级别），闸门时间0.5s

第2个模块：被测信号频率为1022494.88Hz（MHz级别），闸门时间0.5ms

第3个模块：被测信号频率为76103.5Hz（KHz级别），闸门时间0.5s

第4个模块：被测信号频率为21.217Hz（Hz级别），闸门时间0.5s

//多变量对比测试
`timescale 1ns/1ns//时间单位/精度

//------------<模块及端口声明>----------------------------------------
module tb_cymometer_direct();

reg sys_clk;
reg sys_rst_n;
reg         clk_fx1;
reg     clk_fx2;
reg        clk_fx3;
reg     clk_fx4;

wire [31:0]fre1;
wire [31:0]fre2;
wire [31:0]fre3;
wire [31:0]fre4;

 defparam cymometer_direct_inst2.TIME_GATE = 500_000;          //重设闸门时间1ms

//------------<例化被测试模块>----------------------------------------
cymometer_directcymometer_direct_inst1(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx1),

.fre       (fre1)
);

cymometer_directcymometer_direct_inst2(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx2),

.fre       (fre2)
);

cymometer_directcymometer_direct_inst3(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx3),

.fre       (fre3)
);

cymometer_directcymometer_direct_inst4(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx4),

.fre       (fre4)
);
//------------<例化被测试模块>----------------------------------------

//------------<设置初始测试条件>----------------------------------------
initial begin
sys_clk = 1'b0;//初始时钟为0
sys_rst_n <= 1'b0;//初始复位
clk_fx1<= 1'b0;
clk_fx2<= 1'b0;
clk_fx3<= 1'b0;
clk_fx4<= 1'b0;
#5//5个时钟周期后
sys_rst_n <= 1'b1;//拉高复位，系统进入工作状态

end
//------------<设置时钟>----------------------------------------------
always #10 sys_clk = ~sys_clk;//系统时钟周期20ns

always #489 clk_fx1 = ~clk_fx1;//被测信号周期489*2ns，理论频率1022494.88Hz（MHz级别）
always #489 clk_fx2 = ~clk_fx2;//被测信号周期489*2ns，理论频率1022494.88Hz（MHz级别）

always #6570 clk_fx3 = ~clk_fx3;//被测信号周期6570*2ns，理论频率76103.5Hz（KHz级别）
always #23565678 clk_fx4 = ~clk_fx4;//被测信号周期23565678*2ns，理论频率21.217Hz（Hz级别）

endmodule

测量结果如下：

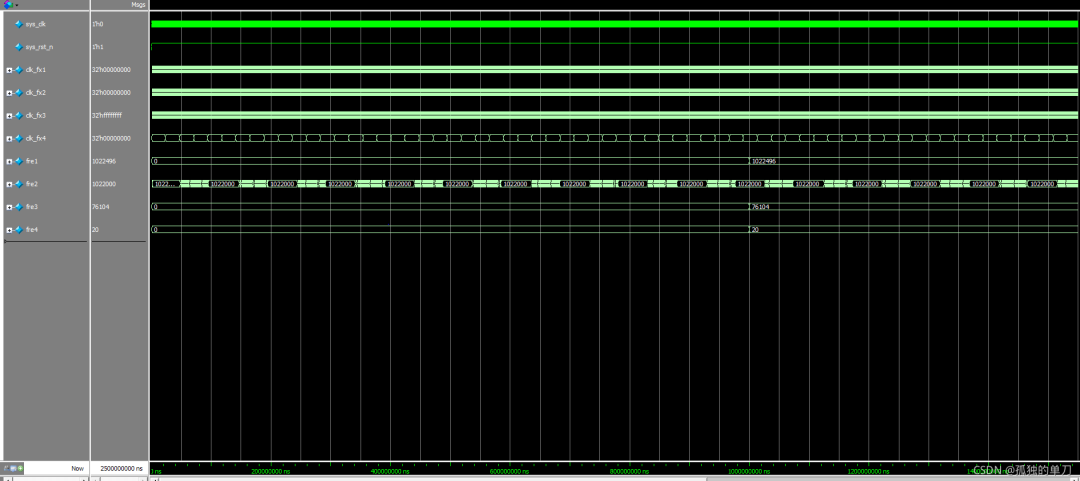
将测量结果整理成下表：

	闸门时间	理论频率（Hz）	实际测量频率（Hz）	测量误差
模块1	0.5s	1022494.88	1022496	1.095e-4%
模块2	0.5ms	1022494.88	1022000	4.840e-4%
模块3	0.5s	76103.5	76104	6.570e-4%
模块4	0.5s	21.217	20	5.736%

从上表的测试结果可以对直接测量法做出如下总结：

闸门时间越长，测量结果越精准，但是也会导致单次测量时间过长

直接测量法适合测量高频信号，测量误差与闸门时间及被测信号频率相关

3、间接测量法

3.1、方法

间接测量法也叫周期测量法，即在一个被测信号的周期内，测量基准时钟的个数，得到被测信号的周期，再将其转化为频率。

下图中的信号分别为：

sys_clk：系统的基准时钟

clk_fx：被测信号

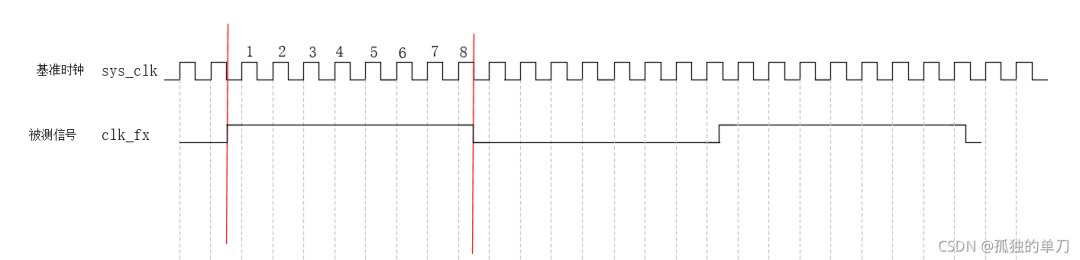
在被测信号clk_fx为高电平的时间内，使用基准时钟进行计数，计数个数为cnt（图中为8），则cnt基准时钟周期=半个被测信号的周期。

所以cnt/ FERQ_SYS(基准时钟频率)=(1/2) * (1/clk_fx)，化简后clk_fx =FERQ_SYS/（cnt*2）

此种方法适用于测量低频信号，但同时也会带来测量速度过慢的问题，误差来自一个系统基准时钟。

3.2、误差分析

从图可以看出，在被测信号高电平期间，被测信号实际上差不多有8.5个周期被囊括在内，但是因为被测信号是相对与系统的异步信号，相位不同，所以实际采样为8，这样造成的误差为1个基准信号周期。可以预见，这种测量方法带来的测量误差即为一个基准信号周期。

那么理论上测得的准确频率：clk_fx =FERQ_SYS/（cnt*2）----理论上cnt无误差

实际上测量的频率值：clk_fx =FERQ_SYS/（（cnt±1）*2）----cnt会存在一个周期的测量误差

测量误差 = |（clk_fxe -clk_fx）/clk_fxe | 100% = 1 / cnt 100%

所以测得的cnt越大，那么测出来的误差值就小，而cnt越大则代表被测信号的频率越低（周期越高），所以可以推断该种测量方法适合测量低频信号。

2.3、Verilog代码

Verilog源码如下：

在被测信号计数高电平期间使用基准时钟计数

在被测信号计数低电平期间更新测量数据

使用parameter定义参数，方便调用修改

//间接测量法(低频)
module cymometer_indirect(
input sys_clk,//基准时钟，设计为50M(可更改)
input sys_rst_n,   //复位信号，低电平有效
                                    //待测信号
input clk_fx,//测量结果
output reg [31:0]fre
);

parameterTIME_SYS  = 20;//系统时钟周期：20ns--频率=50MHz

reg [31:0]cnt_fx;//对被测信号高电平进行计数的计数器

//在测信号高电平期间进行计数
always @(posedge sys_clk or negedge sys_rst_n)begin
if(!sys_rst_n)
cnt_fx <= 0;
else if(clk_fx)
cnt_fx <= cnt_fx+1;
else
cnt_fx <= 0;
end
//在测信号低电平期输出测量数据
always @(negedge clk_fx or negedge sys_rst_n )begin
if(!sys_rst_n)
fre<=0;
else
fre<=1000_000_000/(TIME_SYS*cnt_fx*2);
end
 
endmodule

3.4、仿真分析

Testbench依然采用在直接测量法测试用的3个频率设置

模块1被被测信号周期23565678*2ns，理论频率21.217Hz（Hz级别）

模块2被测信号周期6570*2ns，理论频率76103.5Hz（KHz级别）

模块3被测信号周期489*2ns，理论频率1022494.88Hz（MHz级别）

`timescale 1ns/1ns//时间单位/精度

//------------<模块及端口声明>----------------------------------------
module tb_cymometer_indirect();

reg sys_clk;
regsys_rst_n;
regclk_fx1;
regclk_fx2;
regclk_fx3;

wire [31:0]fre1;
wire [31:0]fre2;
wire [31:0]fre3;

//------------<例化被测试模块>----------------------------------------
cymometer_indirectcymometer_indirect_inst1(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx1),

.fre       (fre1)
);

cymometer_indirectcymometer_indirect_inst2(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx2),

.fre       (fre2)
);

cymometer_indirectcymometer_indirect_inst3(
.sys_clk(sys_clk),
.sys_rst_n(sys_rst_n),
.clk_fx(clk_fx3),

.fre       (fre3)
);

//------------<设置初始测试条件>----------------------------------------
initial begin
sys_clk = 1'b0;//初始时钟为0
sys_rst_n <= 1'b0;//初始复位
clk_fx1<= 1'b0;
clk_fx2<= 1'b0;
clk_fx3<= 1'b0;
#5//5个时钟周期后
sys_rst_n <= 1'b1;//拉高复位，系统进入工作状态

end
//------------<设置时钟>----------------------------------------------
always #10 sys_clk = ~sys_clk;//系统时钟周期20ns

always #23565678 clk_fx1 = ~clk_fx1;//被测信号周期23565678*2ns，理论频率21.217Hz（Hz级别）
always #6570 clk_fx2 = ~clk_fx2;//被测信号周期6570*2ns，理论频率76103.5Hz（KHz级别）
always #489 clk_fx3 = ~clk_fx3;//被测信号周期489*2ns，理论频率1022494.88Hz（MHz级别）

endmodule

仿真如下图1：

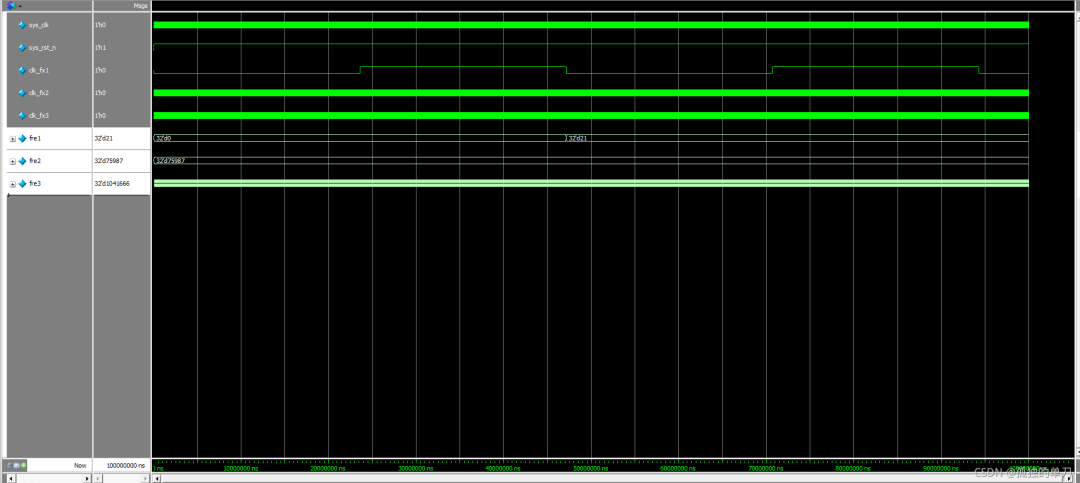
将测量结果整理成下表：

	理论频率（Hz）	实际测量频率（Hz）	测量误差
模块1	21.217297	21	1.02%
模块2	76103.5	75987	0.15%
模块3	1022494.88	1041666	1.87%

从上表的测试结果可以对间接测量法做出如下总结：间接测量法适合测量低频信号，测量误差与测信号频率相关。

需要注意的是，输出信号不能处理浮点数，推荐的解决办法是将其放大整数倍（100倍），以便实现小数点的频率测量(不然小数点被截断会带来额外的误差)。

将测量结果乘以1000，一定程度上消除小数截断带来的误差，模块1的测试结果为21.217Hz，测量误差为1.9998e-3%，大大低于另外两个高频信号。（这里不给出具体的测试过程了，可以自己尝试下）。

4、等精度测量法

4.1、概念

上述两种方法都会产生±1 个被测时钟周期的误差，在实际应用中有一定的局限 性；而且根据两种方式的测量原理，很容易发现频率测量法适合于测量高频时钟信号，而周期测量法适合于低频时钟信号的测量，但二者都不能兼顾高低频率同样精度的测量要求。

等精度测量法与前两种方式不同，其最大的特点是，测量的实际门控时间不是一个固 定值，它与被测时钟信号相关，是被测时钟信号周期的整数倍。在实际门控信号下，同时对标准时钟和被测时钟信号的时钟周期进行计数，再通过公式计算得到被测信号的时钟频率。 由于实际门控信号是被测时钟周期的整数倍，就消除了被测信号产生的±1 时钟周期的误差，但是会产生对标准时钟信号±1时钟周期的误差，而标准时钟通常又是频率极高，所以误差较之前两种方法就大大降低。

此种测量方法相对误差与被测信号频率的大小无关，仅与闸门时间和基准时钟频率有关，即实现了整个测试频段的等精度测量。闸门时间越长，基准时钟频率越高，测频的相对误差越小。需要注意的是，原则上门控时间越长，则精度越高，但测量低频信号（Hz级别）时，建议将门控时间设置为被测信号的十几倍即可，否则测量时间将会过长。

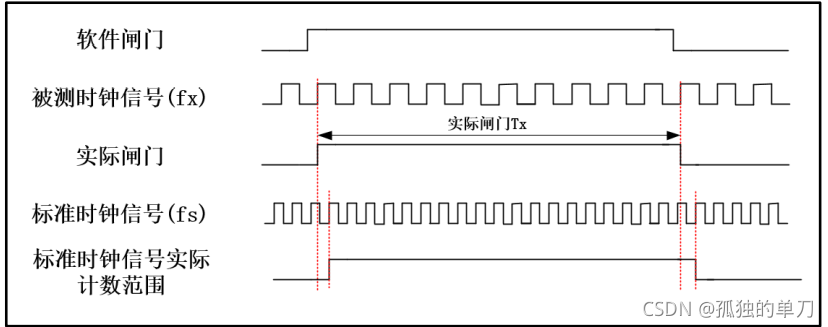
了解了等精度测量原理之后，我们来说明一下被测时钟信号的计算方法：

首先通过被测信号生成实际闸门

分别对实际闸门下被测时钟信号和标准时钟信号的时钟周期进行计数。

实际闸门下被测时钟信号周期数为 X，设被测信号时钟周期为 Tfx，它的时钟频率 fx = 1/Tfx，由此可得等式：X * Tfx = X / fx = Tx（实际闸门）----这里无误差。

实际闸门下标准时钟信号周期数为 Y（误差为1），设被测信号时钟周期为 Tfs，它的时钟频率 fs = 1/Tfs，由此可得等式：Y * Tfs = Y / fs = Tx（实际闸门）----这里最大误差为1个基准时钟周期。

将两等式结合得到只包含各自时钟周期计数和时钟频率的等式：X / fx = Y / fs = Tx(实际闸门)，等式变换，得到被测时钟信号时钟频率计算公式：fx = X * fs / Y。

将已知量标准时钟信号时钟频率 fs 和测量量 X、Y 带入计算公式，得到被测时钟信号时钟频率 fx。

4.2、误差分析

根据前文及上图，不难发现，误差来源于使用基准时钟在闸门时间测量时会存在一个基准时钟周期的误差。

那么理论上测得的准确频率：clk_fxe = X * fs / Y----理论上Y无误差

实际上测量的频率值：clk_fx = X * fs / Y----Y会存在1个周期的测量误差

测量误差 = |（clk_fxe - clk_fx）/ clk_fxe | 100% = 1 / Y 100%

所以测得的Y越大，那么测出来的误差值就小。当闸门时间越大，Y越大；基准时钟频率越高，Y越大。所以通过提高基准时钟频率或者增加闸门时间（但是会使测量过长，需要取舍），可以有效提高测量精度。

4.3、Verilog代码

Verilog源码如下：

//等精度测量法(低频)
module cymometer_equal (   
        input                 clk_fs ,    
        input                 rst_n  ,            
        input                 clk_fx , 

        output   reg [63:0]   fre      
);

parameterCLK_FS    = 26'd50_000_000;           
parameter   GATE_TIME = 16'd100;    //门控时间，越大误差越小，但测量时间也会变长    

//reg define
reg                gate_fx;   //门控信号，被测信号域下         
reg                gate_fs     ;           //同步到基准时钟的门控信号
reg                gate_fs_r   ;          //用于同步gate信号的寄存器
reg                gate_fs_d0  ;           //用于采集基准时钟下gate下降沿
reg                gate_fs_d1  ;           //用于采集基准时钟下gate下降沿
reg                gate_fx_d0  ;          //用于采集被测时钟下gate下降沿
reg                gate_fx_d1  ;           //用于采集被测时钟下gate下降沿
reg    [15:0]   gate_cnt    ;          //门控计数
reg    [31:0]   fs_cnt      ;           //门控时间内基准时钟的计数值
reg    [31:0]   fs_cnt_temp ;           //fs_cnt 临时值
reg    [31:0]   fx_cnt      ;           //门控时间内被测时钟的计数值
reg    [31:0]   fx_cnt_temp ;           //fx_cnt 临时值

//wire define
wire               neg_gate_fs;            //基准时钟下门控信号下降沿=
wire               neg_gate_fx;            //被测时钟下门控信号下降沿

//捕捉信号下降沿
assign neg_gate_fs = gate_fs_d1 & (~gate_fs_d0);
assign neg_gate_fx = gate_fx_d1 & (~gate_fx_d0);

//检测gate_fx下降沿
always @(posedge clk_fx or negedge rst_n) begin
    if(!rst_n) begin
        gate_fx_d0 <= 1'b0;
        gate_fx_d1 <= 1'b0;
    end
    else begin
        gate_fx_d0 <= gate_fx;
        gate_fx_d1 <= gate_fx_d0;
    end
end
//检测gate_fs下降沿
always @(posedge clk_fs or negedge rst_n) begin
    if(!rst_n) begin
        gate_fs_d0 <= 1'b0;
        gate_fs_d1 <= 1'b0;
    end
    else begin
        gate_fs_d0 <= gate_fs;
        gate_fs_d1 <= gate_fs_d0;
    end
end
//被测时钟闸门计数器
always @(posedge clk_fx or negedge rst_n) begin
    if(!rst_n)
        gate_cnt <= 16'd0; 
    else if(gate_cnt == GATE_TIME*2)
        gate_cnt <= 16'd0;
    else 
        gate_cnt <= gate_cnt + 1'b1;
end
//被测时钟闸门生成
always @(posedge clk_fx or negedge rst_n) begin
    if(!rst_n)
        gate_fx <= 1'b0;     
    else if(gate_cnt == GATE_TIME)
        gate_fx <= 1'b1;
    else if(gate_cnt == GATE_TIME*2)
        gate_fx <= 1'b0;
    else 
        gate_fx <= gate_fx;
end
//把闸门从被测时钟域同步到基准时钟域
always @(posedge clk_fs or negedge rst_n) begin
    if(!rst_n) begin
        gate_fs_r <= 1'b0;
        gate_fs   <= 1'b0;
    end
    else begin
        gate_fs_r <= gate_fx;
        gate_fs   <= gate_fs_r;
    end
end
//在被测时钟域对被测信号计数
always @(posedge clk_fx or negedge rst_n) begin
    if(!rst_n) begin
        fx_cnt_temp <= 0;
        fx_cnt <= 0;
    end
    else if(gate_fx)
        fx_cnt_temp <= fx_cnt_temp + 1'b1;
    else if(neg_gate_fx) begin
        fx_cnt_temp <= 0;
        fx_cnt <= fx_cnt_temp;
    end
end
//在基准时钟域对基准时钟计数
always @(posedge clk_fs or negedge rst_n) begin
    if(!rst_n) begin
        fs_cnt_temp <= 0;
        fs_cnt <= 0;
    end
    else if(gate_fs)
        fs_cnt_temp <= fs_cnt_temp + 1'b1;
    else if(neg_gate_fs) begin
        fs_cnt_temp <= 0;
        fs_cnt <= fs_cnt_temp;
    end
end
//在基准时钟域输出结果
always @(posedge clk_fs or negedge rst_n) begin
    if(!rst_n) begin
        fre <= 0;
    end
    else if(gate_fs == 1'b0)
        fre <= (CLK_FS * fx_cnt ) / fs_cnt;
end

endmodule

4.4、仿真分析

Testbench：

设计被测信号周期为489*2=978ns，则其理论频率为1/978ns=1022494.88Hz

`timescale 1 ns/ 1 ns
//------------<模块及端口声明>----------------------------------------
module tb_cymometer_equal();

reg clk_fs;
reg clk_fx;
reg rst_n;
                                              
wire [63:0]  fre;

//------------<例化被测试模块>----------------------------------------                          
cymometer_equal cymometer_equal_inst ( 
.clk_fs(clk_fs),
.clk_fx(clk_fx),
.fre(fre),
.rst_n(rst_n)
);
//------------<设置初始测试条件>----------------------------------------
initialbegin                                                  
clk_fs = 1'b0;
clk_fx <= 1'b0;
rst_n <= 1'b0;
#116 
rst_n <= 1'b1;

end 
//------------<设置时钟>----------------------------------------------                                                   
always#10 clk_fs <= ~clk_fs;                                     
always  #489 clk_fx <= ~clk_fx;  
                                                 
endmodule

仿真结果如下所示

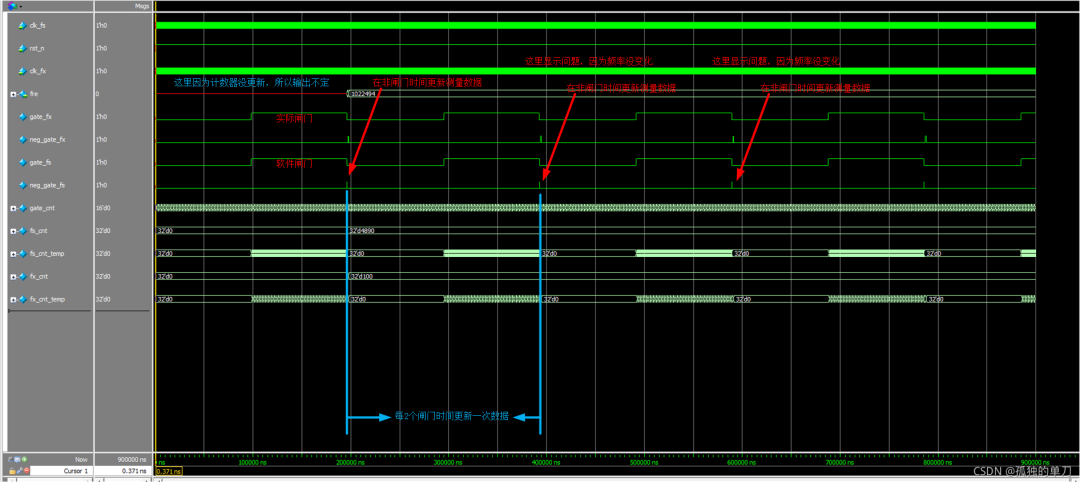
上图的测量结果为1022494Hz，理论频率为1/978ns=1022494.88Hz，可以看到这个结果相当精确。

接下来更改一下Testbench，比较一下闸门时间对被测信号的影响以及被测信号自身频率高低对测量的影响（为避免仿真时间过长，闸门时间均设为10个被测信号周期，因为基准时钟频率较高，所以闸门时间少点不会有什么影响）

第1个模块：被测信号频率为1022494.88Hz（MHz级别）

第2个模块：被测信号频率为76103.5Hz（KHz级别）

第3个模块：被测信号频率为21.217Hz（Hz级别）

仿真结果如下：

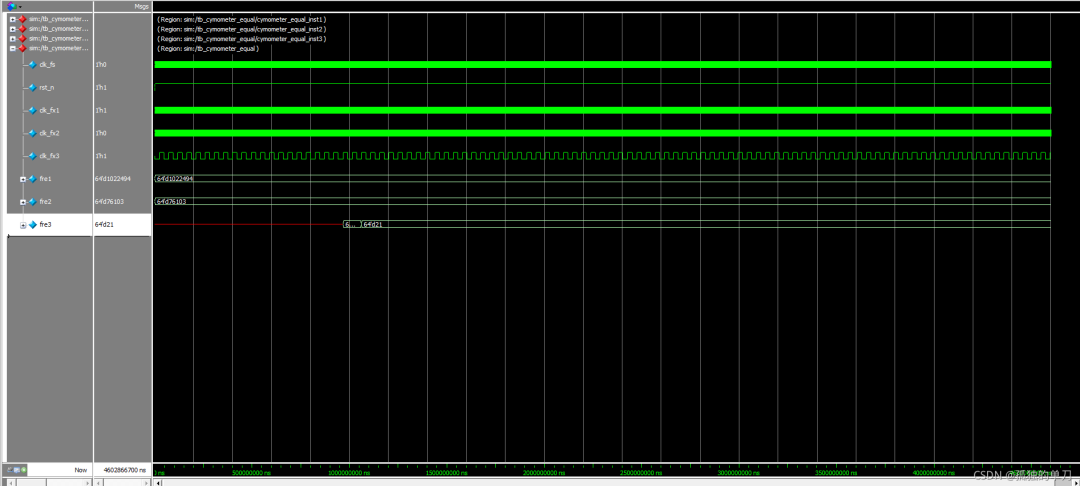
将测量结果整理成下表：

	理论频率（Hz）	实际测量频率（Hz）	测量误差
模块1	1022494.88	1022494	8.60e-5%
模块2	76103.5	76103	6.57e-4%
模块3	21.217297	21	1.02%

从上表的测试结果发现等精度测量法同时适用于高低频域，测量结果误差只和基准时钟频率有关。

这里需要注意的是，因为测量结果都是整数（FPGA自动截断小数），如果被测频率较低，那么因为小数被截断，会使得误差增大。一个比较方便的解决办法是把计算公式都放大一定的倍数，从而使得“小数点前移”。 将测量结果乘以1000，一定程度上消除小数截断带来的误差，模块3的测试结果为21.217Hz，测量误差为1.9998e-3%，基本和另外两个信号处于同一数量级。（这里不给出具体的测试过程了，可以自己尝试下）。

5、总结

直接测量法适合测量高频信号；频率越高、测量时间越长，测量结果越精准；

间接测量法适合测量低频信号，但测量精度取决于自身频率；

等精度测量法相对误差与被测信号频率的大小无关，仅与闸门时间和基准时钟频率有关，即实现了整个测试频段的等精度测量。闸门时间越长，基准时钟频率越高，测频的相对误差就越小。