半导体雷射相对强度杂讯

从前面一小节对半导体雷射线宽的讨论可以知道，即使半导体雷射操作在稳态的状况下，还是会有因为自发辐射所引起的相位的杂讯，除此之外，雷射操作的杂讯来源很多，例如雷射共振腔中的载子和光子产生和复合的事件是不断地发生，而这些瞬间的变化会使得半导体雷射的载子、光子与相位彼此互相影响并产生杂讯。因此：我们可以使用Langevin杂讯源于载子与光子的速率方程式中，这些Langevin杂讯可以视为在时域上乱数随机产生的扰动，为AC型态的函数，相对的，在频域中Langevin杂讯源为极宽频的白杂讯（white noise），也就是其强度平均分布到所有频率上。若雷射处于稳态状态，这些由载子的Langevin杂讯Fn（t）与光子的Langevin杂讯Fp（t）将会驱动小信号的变化，因此我们可以改写（4-48）式与（4-49）式的小信号模型并去除外部输入电流的调制项：

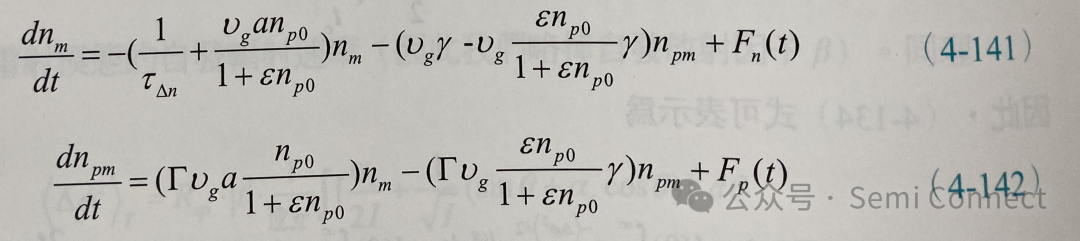
若使用（4-50）式到（4-53）式的定义，可以将上两式写成矩阵形式：

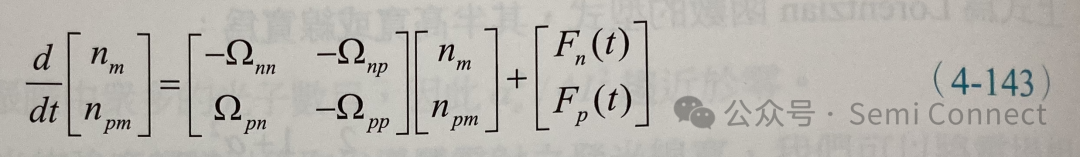
转换到频域中，可以得到：

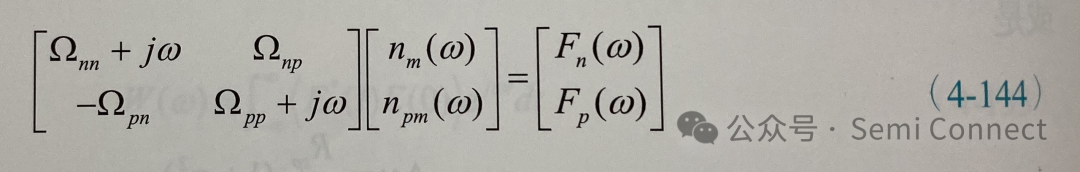
由此可以解得nm与npm：

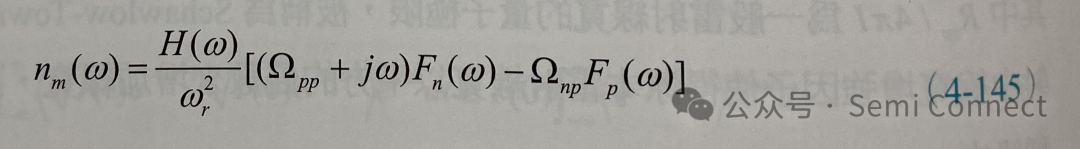
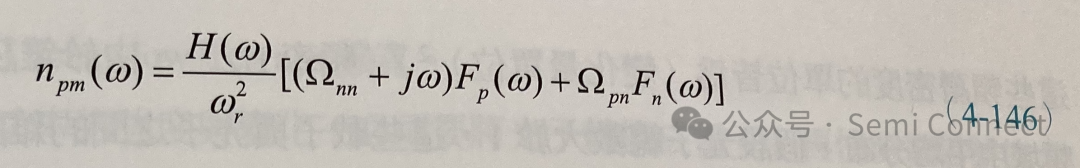
其中wr为前面所定义的弛豫频率，H（w）同（4-23）式。由于载子变化与光子变化的频谱密度（spectral density）可以表示成：

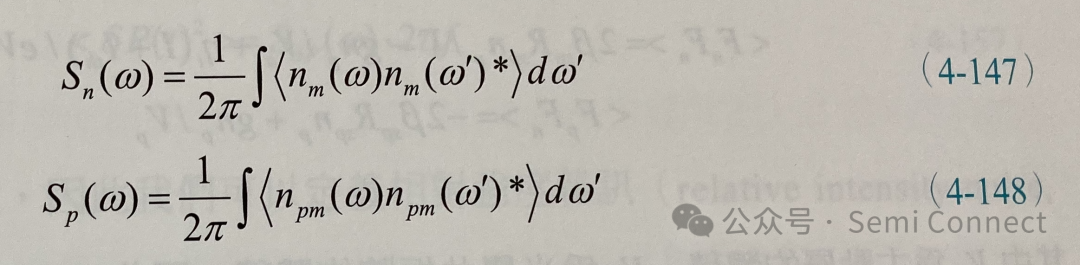
上两式中的＜>括号表示对时间平均，因此将（4-145）式与（4-146）式分别代入（4-147）式与（4-148）式，我们可以得到共振腔中载子浓度与光子密度变化的小信号频谱密度：

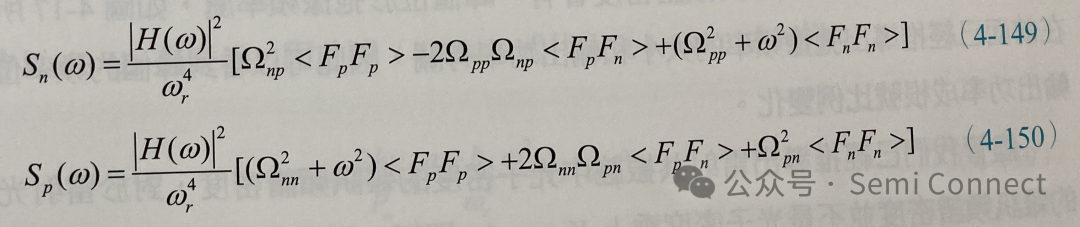
这些频谱密度的单位皆为（变化量单位）2/（频率Hz）。由于鸡讯的频谱密度＜FiFj＞在频域中平均分布，假设光子总数大于1，这些载子与光子之间的杂讯关联强度可以估计为

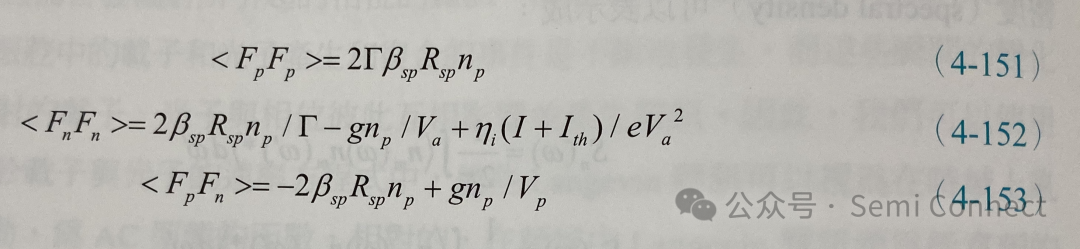
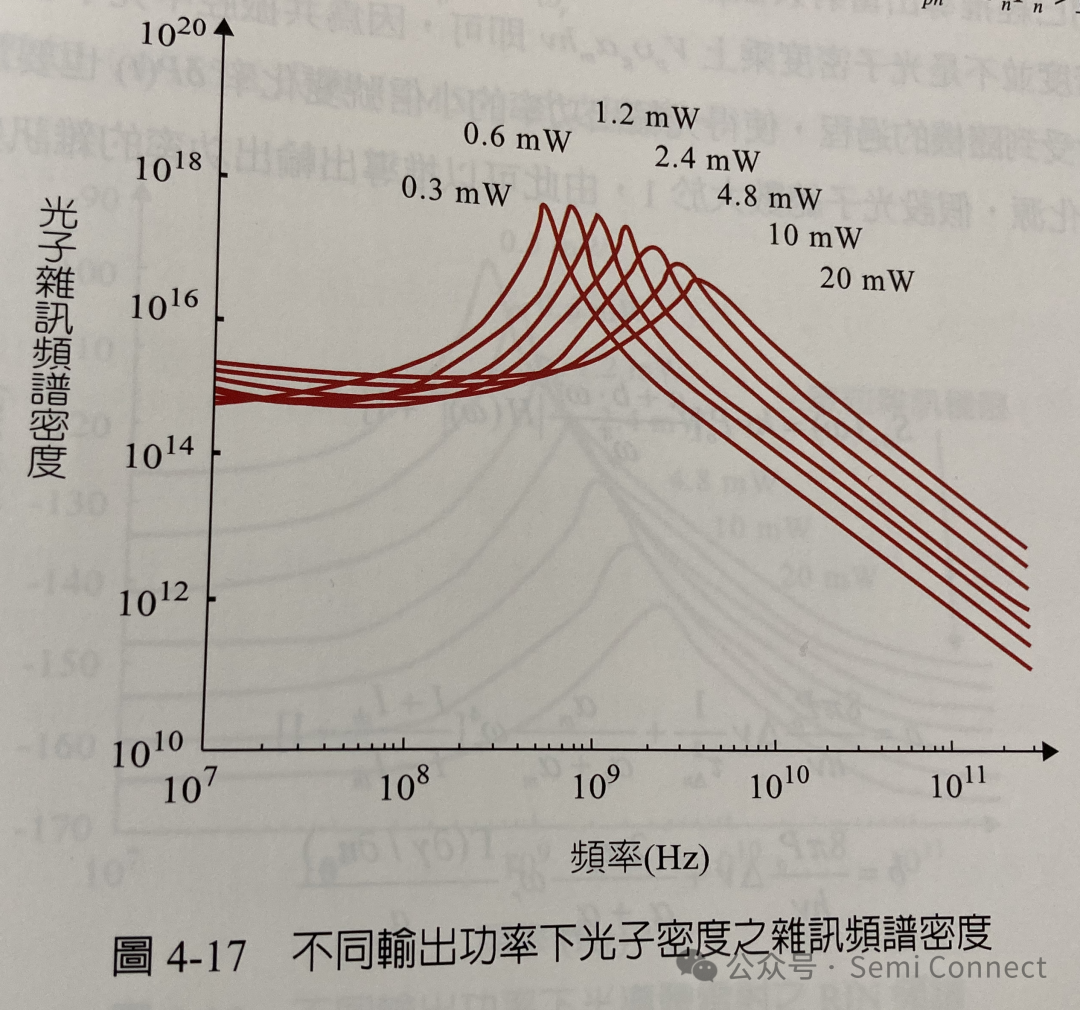
其中Va为主动层的体积、Vp为光学共振腔的体积，这些杂讯基本上都是来自载子与光子中因随机产生或复合所造成的散粒杂讯（shot noise）。观察（4-149）式与（4-150）式可知・载子浓度与光子密度的杂讯频谱密度和【a+bw2】｜H（w）｜2有关，其中a和b不含频率项，其频谱密度会有一峰值位于弛豫频率处，如图4-17所示，我们在前面已经推导出弛豫频率的大小和输出功率有关，因此可以看到峰值的频率位置会随着输出功率成根号比例变化。

尽管我们已经推导出雷射共振腔中光子密度的杂讯频谱密度，对于雷射光输出功率的杂讯频谱密度并不是光子密度乘上VpUgamhv即可，因为共振腔中光子在通过有限反射率的镜面时会受到随机的过程，使得光输出功率的小信号变化率P（t）也要加上Langevin杂讯的AC变化源，假设光子总数大于1，由此可以推导出输出功率的杂讯频谱密度如下：

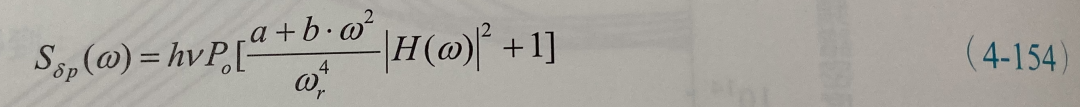
其中

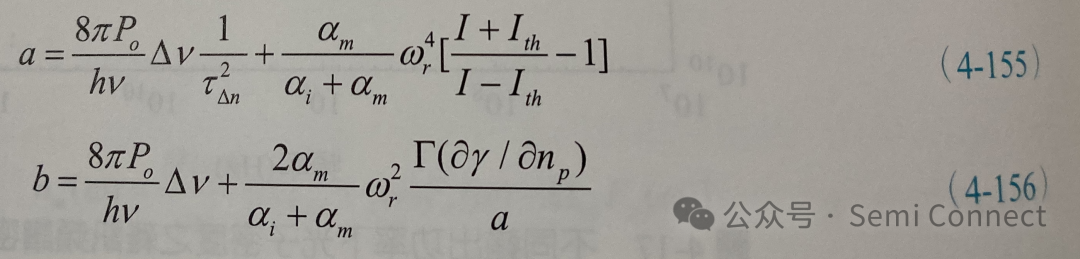
而△v为前一小节介绍的Schawlow-Townes线宽。

一般而言要侦测光功率的强度与变化，必须要将光子转换成电子，再侦测电信号的大小与 变化：

其中△f为量测设备的频宽，因此我们可以定义相对强度杂讯 （relative intensity noise，RIN）为：

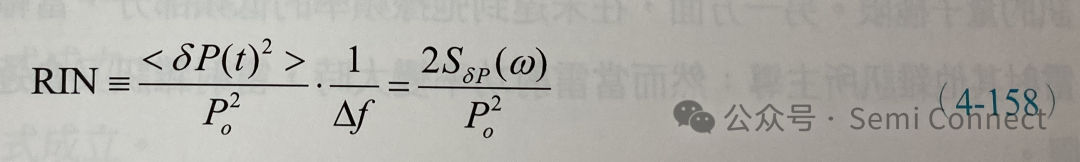
通常RIN会以dB/Hz来表示。因此将（4-154）式代入（4-158）式可得：

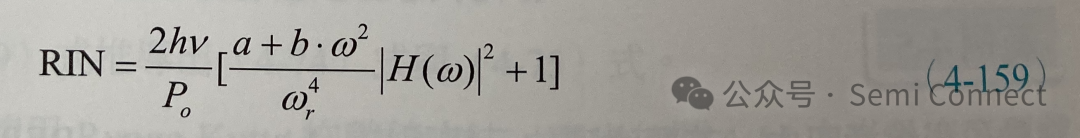
其中a和b常数如（4-155）式与（4-156）式之定义。

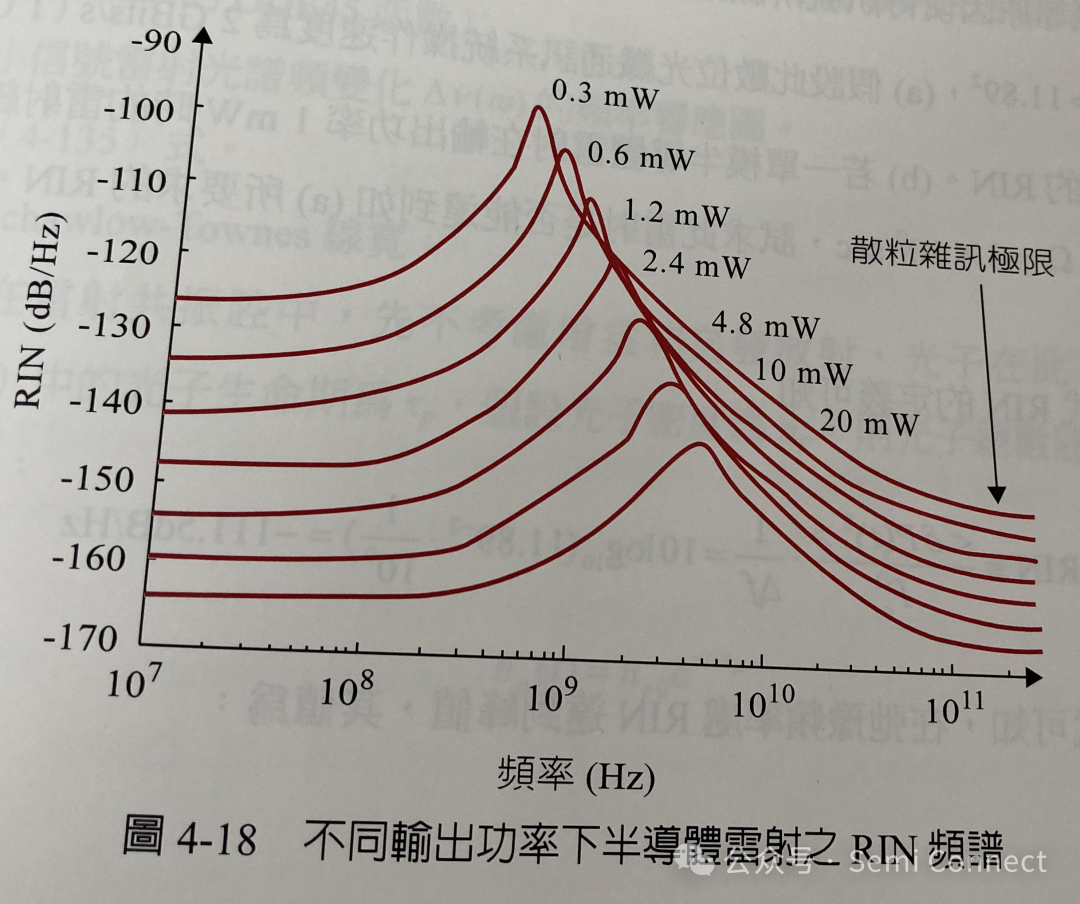
图4-18为半导体雷射在不同输出功率下的RIN频谱图，我们首先看到RIN频谱中的峰值位置为弛豫频率，同样的峰值的频率位置会随着输出功率成根号比例变化。当w=wr时，（4-159）式可以近似成：

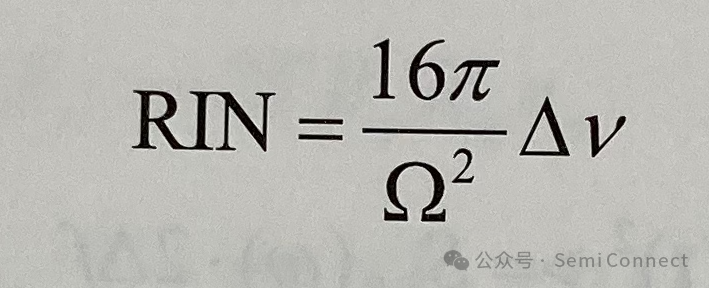
由于阻尼系数Ω大约和输出功率P0成正比，因此当输出功率增加时，RIN会以1/P03的此例减少。

RIN会在弛豫频率达到最大值，在超过弛豫频率的高频部分，杂讯会逐渐达到散粒杂讯的量子极限。另一方面，在未达到弛豫频率的低频部分，当输出功率很低时，杂讯会被雷射其他杂讯所主导；然而当雷射功率变大时，雷射杂讯又会逐渐达到散粒杂讯的量子极限。