光栅化的基础思想与三维场景的基本流程

数学上的规定：

由于习惯的不同，每个人对同一个事物的标准也不同。

应事先规定好整个项目的一些“习惯”，并坚决贯彻它们，上下统一。

世界坐标系：

场景中所有物体处于世界坐标系下，且所有的坐标系均为左手坐标系，左手坐标系三个轴的指向如图：

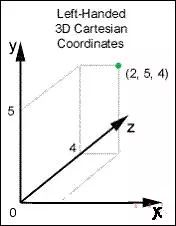
以屏幕为基准，该坐标系X轴指向右，Y轴指向上，Z轴指向屏幕里面。

以此坐标系我们可以创建一个世界空间。当然并没有真正创建出来，只是一个约定，便于日后的使用。就像地球的经纬度一样，有了这个我们就能描述什么东西在什么地方了。

物体坐标系：

而世界中有很多物体，比如游戏中的模型，玩家等等。

该世界里的每个物体都含有三个数据：

1）该物体中心处于世界的位置(x,y,z)

2）该物体旋转的角度(Pitch,Yaw,Roll)。分别对应绕x y z轴旋转的角度，并规定从各个轴的负方向看过去的顺时针方向为正。比如(0,0,90)代表该物体不沿x y轴旋转，只沿z轴旋转90度，且旋转方向为顺时针。

3）构成该物体的所有点的相对于物体中心的位置(xi, yi, zi) (i 为构成物体的各个点，比如正方体的 8 个顶点）

光栅化的基础思想

（假设世界坐标系下只有一个物体，简化描述）：

1）将该物体的所有点根据该物体在世界的位置及朝向进行缩放、旋转和平移，这一步将把物体的所有点的坐标从物体坐标系转换到世界坐标系。

比如某物体只有一个点，该点处于相对物体中心的 (1,0,0) 处，而该物体中心处于世界的 (0,1,0) 处，且没有经过旋转。那么该点经过缩放、旋转和平移的坐标转换后，可以得到该点在世界坐标系下的位置 (1,1,0) 。

2）将世界中的观察者（人、玩家、摄像机等等）简化成一个点，就像一个摄像机，该摄像机便是观察的视线发出的地方。同时摄像机也有如物体一样的位置信息 (x,y,z) 及旋转角度信息 (pitch, yaw, roll)。通过这两组数据我们可以求出摄像机在世界坐标系下的位置以及视线的朝向。

但将要进行的动作恰恰相反，我们将世界的所有点（经过第一步后这些点的坐标系已经从他们的物体坐标系转换到了世界坐标系）进行上述变换的逆变换，可以得到以摄像机为中心的所有点的坐标。这一步之后的世界空间改叫观察空间。

3）将观察空间转至齐次剪裁空间。在实际生活中摄像机（或者人类）看东西的范围是有限的。但是目前为止所有的点不论摄像机看不看得到，都经过了变换。所以还要将观察空间中的所有点转换到一个叫做齐次剪裁空间的空间。这个空间有一个长宽高均为2的人为划定的范围，且该立方体形的范围的中心处于原点(0,0,0)。

也就是说，这个范围上下前后左右的范围是 -1 到 1 。经过一个特殊的矩阵乘法变换后，所有处于该 2x2x2 立方体形范围内的所有点，都将是看得到的，最终会被渲染出来的。所有不在该 2x2x2 大小的范围内的点，都处于视线之外，最后都将不会渲染出来。盗张图：

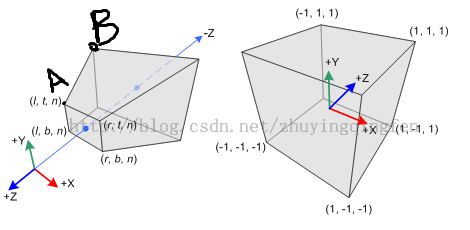
左边是观察空间，原点处是我们的摄像机（这个坐标系不是我们使用的左手坐标系，这是右手坐标系，他的 z 轴朝向屏幕外）。右边是第三步转换后形成的齐次剪裁空间。

目前已经把所有点都转换到了这个齐次剪裁空间，并且剪裁掉了一切不在该立方体包围内的点。

这时候我们已经可以把各个点的x、y坐标拿来，经过插值匹配到显示器的分辨率后（即将每个点的x y坐标的数值从[-1,1]“拉伸”至譬如[0,1920]和[0,1080]），直接显示出来了。但是显示的结果会比较奇怪，远近不同的物体大小居然一样。该投影过程叫做正交投影，而日常生活中我们所看到的近大远小的世界是透视投影的结果。

怎么进行透视投影？大致思路是将每个点的在观察空间下的z坐标拿来，除以该点在齐次剪裁空间下的x和y的值（x = x/z, y = y/z）。显示出来便是透视投影后的图像。

简短总结：

要想将构成三维世界的点转换到显示器这个二维平面上来，需要对每个点进行如下操作

1）物体空间转换至世界空间 （通过数个矩阵乘法）

2）世界空间转换至观察空间 （需求出摄像机变换的逆矩阵）

3）观察空间转换至齐次剪裁空间 （通过乘上特殊的变换矩阵）

4）进行透视除法 （除以特定 z 值）

但是以上变换只是得到了点最终的位置信息。要想显示在屏幕上，还需要填充点和线组成的面，甚至是赋上自定义的贴图。