功率电子转换器可以视为由分段线性元件(传统元件如电阻、电感和电容是特例)与电压源、电流源、二极管和电子开关(如晶闸管、晶体管、MOSFET等)组成。
在此背景下,我们将电子设备(ED)定义为任何具有分段线性电流-电压特性的电气或电子元件,尽管这可能是一个不太精确的术语。在许多实际情况下,电子设备可以建模为一个可变电阻,其在导通状态下的值非常低,而在阻断状态下的值非常高。在其他情况下,可能需要使用更详细的半导体模型来表示设备。然而,在系统层面,特别是在建模、仿真和控制设计中,快速切换现象通常不是主要关心的问题。在这些情况下,将二极管和开关视为理想元件更为便利,假设它们在实质上瞬间在打开和关闭状态之间切换。
这种特性赋予了系统模型一种混合性质,结合了离散和连续时间元素。因此,开关电子系统被归类为混合系统。这些系统通过多种拓扑或模式运行,具体取决于开关设备的状态。因此,有必要区分转换器的不同模式,为每种模式开发线性时不变动态模型,并定义系统在模式之间切换的条件。由此过程得到的模型通常被称为开关模型,这是许多功率转换器仿真器(如PLECS)使用的框架。不幸的是,切换的条件可能依赖于状态变量(称为内部控制换相),这使得开关模型变得越来越复杂,即使对于相对简单的转换器拓扑也是如此。
一般来说,构建一个涵盖所有可能操作条件的开关模型(称为完整开关模型)对于具有两个以上电子设备(ED)的转换器来说变得非常具有挑战性。这对于涉及具有内部控制换相特征的电子设备的转换器也是如此。此类场景的一个典型示例是由于某些二极管的阻断状态而发生的间歇导电模式。
相反,互补模型则易于构建,并能够捕捉转换器的所有模式,无需列举它们,也不假设关于模式顺序和切换时间换相时刻的先验知识。构建功率转换器互补模型的关键思想是将非线性设备(包括二极管和开关)的电压-电流特性视为网络动态线性部分的输入-输出,可以利用经典电路理论技术进行建模。模型随后用电子设备的特性进行补充。
构建功率转换器互补模型的方法是将ED的特性与它们所处电路分开建模,然后将这些表示与电路的动态方程整合。在修改后的节点分析中使用了类似的方法,这是在仿真程序(如PSpice)中采用的建模技术,其中ED的特性通过非线性平滑代数关系详细表示。相比之下,在这种方法中,ED被假定为理想的,其特性通过分段仿射关系表示,这是一种为建模和仿真便利而选择的经典方法。
在这种方法中,功率转换器被表示为线性时不变动态系统(记作Σd)的反馈互连,该系统描述电路拓扑,以及一组分段仿射特性(ϕ,λ),表示电子设备(ED)的电流-电压特性(见图1)。在文献中也称为Lur’e模型。
可以使用经典电路理论技术,根据功率转换器的配置推导出Σd的最小状态空间表示。
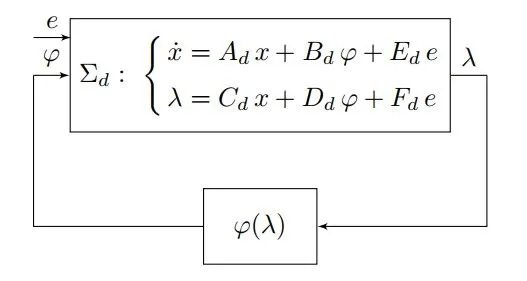 图1
图1非递减的分段仿射ED特性在互补形式中表示,如前一篇文章《开关系统的线性互补模型简介》中所示。
要构建动态块Σd的模型,让我们将每个第i个电子设备(ED)的电流和电压视为输入ϕi或作为电路其余部分的输出λi,后者代表系统的动态部分。通过提取Ns个ED(由线性元件(电阻器、电感器、电容器)和外部源组成),在非常一般的假设下,所获得的电路可以通过状态空间系统描述:
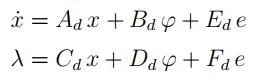
其中,x是状态向量,e表示外部源,ϕ和λ是具有Ns个分量的向量,使得第i个分量对(ϕi,λi)表示第i个ED的特性。
二极管的线性互补模型
理想二极管(ID)的电压-电流特性如图2所示。可以用互补条件简单表示:
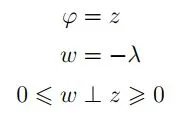
在双重情况下,当λ是ID电流,ϕ是ID电压时,通过改变方程2中两个等式右侧的符号可以得到互补模型。电路的拓扑决定了二极管电流应标记为ϕ(从而影响状态变量的时间导数)还是λ(因此不进入状态的动态方程,而只满足代数方程)。
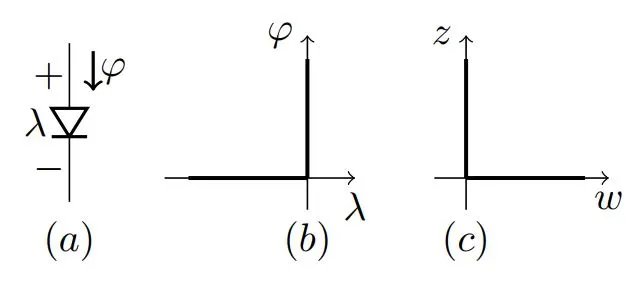 图2
图2示例电路
为了展示这种建模技术在实际应用中的应用,我们可以考虑基于半波整流器的电源,如图3所示。
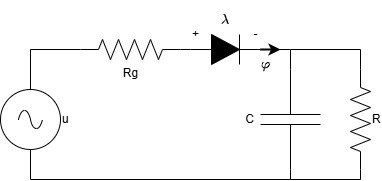 图3
图3通过将进入电容器的电流选择为状态变量,以及将二极管的互补表示用ϕ作为电流,λ作为电压,我们可以使用方程2写出电路的Lur’e表示:
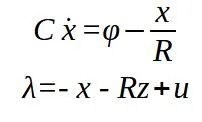 公式3
公式3由此我们最终可以推导出系统的线性互补表示(也称为线性互补系统):
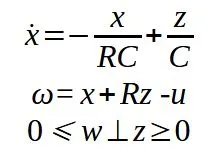 公式4
公式4通过离散化方程4,可以在每个积分步骤中通过解决相应的线性互补问题(LCP)找到解决方案。如所示,一个单一的方程组可以捕捉电路的动态,消除了对二极管每个状态(导电或阻断)详细说明每个等效电路的需要。在经典仿真中(无论是使用可变还是固定步长),求解器必须检测状态的切换(例如,通过电流或电压的零交叉),然后更新下一组方程和状态变量的初始值。然而,由于现代微处理器的计算能力,这种方法不再是问题。此外,所讨论的紧凑表示也对复杂电路的理论分析有价值,因为它使得在一组方程中包含整个系统的动态成为可能。
为了解决这类问题,开发了一种特殊算法,称为Lemke算法。为了提高找到解决方案的性能,可以在Matlab中使用另一个专用求解器,称为“路径”。
仿真结果在以下图中呈现:ϕ和λ在图4中描绘,而在图5中它们相对于最大值进行了归一化,因此可以注意到它们是非负的,并且从未同时为零,因为它们(在这种特定情况下)对应于互补变量,如图2所述。
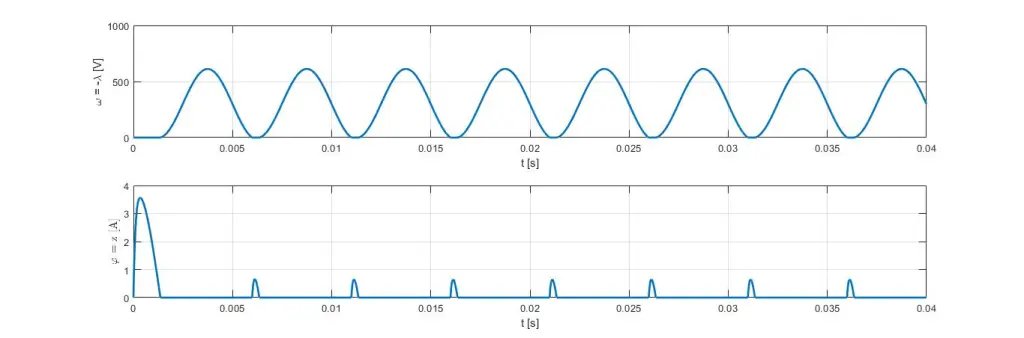 图4
图4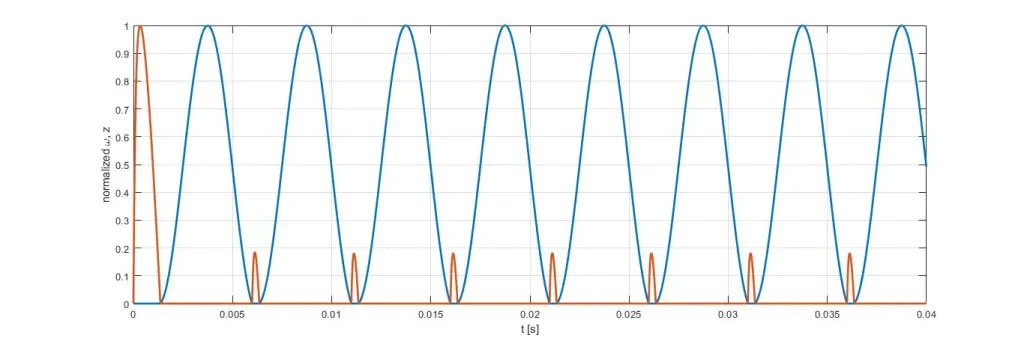 图5
图5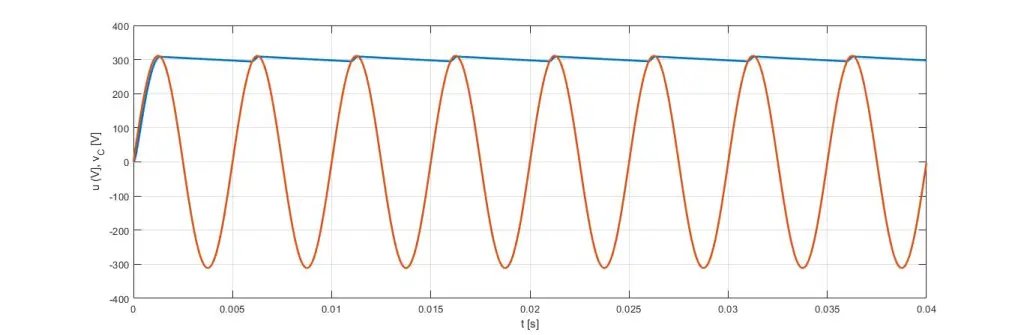 图6
图6结论
大多数功率电子电路可以建模为线性动态系统与静态分段线性特性的反馈互连,这可以使用一组非负互补变量进行描述。集合值函数,例如理想二极管中的电压-电流关系(电压为零时,电流可以取任何非负值,或者电流为零时,电压可以取任何非正值),也可以使用互补变量表示。在这一框架中,可以利用线性互补模型来分析和仿真具有内部切换行为的电路。
-
转换器
+关注
关注
27文章
8808浏览量
149298 -
仿真
+关注
关注
50文章
4177浏览量
134714 -
功率电子
+关注
关注
0文章
51浏览量
11023
发布评论请先 登录
相关推荐
功率型LED热阻测量的新方法
基于线性化技术的二次分配问题求解新方法
提升峰值电流模式控制性能的创新方法





 浮思特 | 创新互补模型:提升功率电子转换器设计与仿真的新方法
浮思特 | 创新互补模型:提升功率电子转换器设计与仿真的新方法












评论