以下是在编程面试中排名前 9 的算法相关的概念,我会通过一些简单的例子来阐述这些概念。由于完全掌握这些概念需要更多的努力,因此这份列表只是作为一个介绍。本文将从Java的角度看问题,包含下面的这些概念:
1. 字符串
2. 链表
3. 树
4. 图
5. 排序
6. 递归 vs. 迭代
7. 动态规划
8. 位操作
9. 概率问题
1. 字符串
如果IDE没有代码自动补全功能,所以你应该记住下面的这些方法。
toCharArray()// 获得字符串对应的char数组
Arrays.sort()// 数组排序
Arrays.toString(char[]a)// 数组转成字符串
charAt(intx)// 获得某个索引处的字符
length()// 字符串长度
length// 数组大小
2. 链表
在Java中,链表的实现非常简单,每个节点Node都有一个值val和指向下个节点的链接next。
classNode{
intval;
Nodenext;
Node(intx){
val=x;
next=null;
}
}
链表两个著名的应用是栈Stack和队列Queue。
栈:
classStack{
Nodetop;
publicNode peek(){
if(top!=null){
returntop;
}
returnnull;
}
publicNode pop(){
if(top==null){
returnnull;
}else{
Nodetemp=newNode(top.val);
top=top.next;
returntemp;
}
}
publicvoidpush(Noden){
if(n!=null){
n.next=top;
top=n;
}
}
}
队列:
classQueue{
Nodefirst,last;
publicvoidenqueue(Noden){
if(first==null){
first=n;
last=first;
}else{
last.next=n;
last=n;
}
}
publicNode dequeue(){
if(first==null){
returnnull;
}else{
Nodetemp=newNode(first.val);
first=first.next;
if(last==temp)last=first;
returntemp;
}
}
}
3. 树
这里的树通常是指二叉树,每个节点都包含一个左孩子节点和右孩子节点,像下面这样:
classTreeNode{
intvalue;
TreeNodeleft;
TreeNoderight;
}
下面是与树相关的一些概念:
平衡 vs. 非平衡:平衡二叉树中,每个节点的左右子树的深度相差至多为1(1或0)。
满二叉树(Full Binary Tree):除叶子节点以为的每个节点都有两个孩子。
完美二叉树(Perfect Binary Tree):是具有下列性质的满二叉树:所有的叶子节点都有相同的深度或处在同一层次,且每个父节点都必须有两个孩子。
完全二叉树(Complete Binary Tree):二叉树中,可能除了最后一个,每一层都被完全填满,且所有节点都必须尽可能想左靠。
译者注:完美二叉树也隐约称为完全二叉树。完美二叉树的一个例子是一个人在给定深度的祖先图,因为每个人都一定有两个生父母。完全二叉树可以看成是可以有若干额外向左靠的叶子节点的完美二叉树。疑问:完美二叉树和满二叉树的区别?
4. 图
图相关的问题主要集中在深度优先搜索(depth first search)和广度优先搜索(breath first search)。
下面是一个简单的图广度优先搜索的实现。
1) 定义GraphNode
classGraphNode{
intval;
GraphNodenext;
GraphNode[]neighbors;
booleanvisited;
GraphNode(intx){
val=x;
}
GraphNode(intx,GraphNode[]n){
val=x;
neighbors=n;
}
publicStringtoString(){
return"value: "+this.val;
}
}
2) 定义一个队列Queue
classQueue{
GraphNodefirst,last;
publicvoidenqueue(GraphNoden){
if(first==null){
first=n;
last=first;
}else{
last.next=n;
last=n;
}
}
publicGraphNode dequeue(){
if(first==null){
returnnull;
}else{
GraphNodetemp=newGraphNode(first.val,first.neighbors);
first=first.next;
returntemp;
}
}
}
3) 用队列Queue实现广度优先搜索
publicclassGraphTest{
publicstaticvoidmain(String[]args){
GraphNoden1=newGraphNode(1);
GraphNoden2=newGraphNode(2);
GraphNoden3=newGraphNode(3);
GraphNoden4=newGraphNode(4);
GraphNoden5=newGraphNode(5);
n1.neighbors=newGraphNode[]{n2,n3,n5};
n2.neighbors=newGraphNode[]{n1,n4};
n3.neighbors=newGraphNode[]{n1,n4,n5};
n4.neighbors=newGraphNode[]{n2,n3,n5};
n5.neighbors=newGraphNode[]{n1,n3,n4};
breathFirstSearch(n1,5);
}
publicstaticvoidbreathFirstSearch(GraphNoderoot,intx){
if(root.val==x)
System.out.println("find in root");
Queuequeue=newQueue();
root.visited=true;
queue.enqueue(root);
while(queue.first!=null){
GraphNodec=(GraphNode)queue.dequeue();
for(GraphNoden:c.neighbors){
if(!n.visited){
System.out.print(n+" ");
n.visited=true;
if(n.val==x)
System.out.println("Find "+n);
queue.enqueue(n);
}
}
}
}
}
5. 排序
下面是不同排序算法的时间复杂度,你可以去wiki看一下这些算法的基本思想。
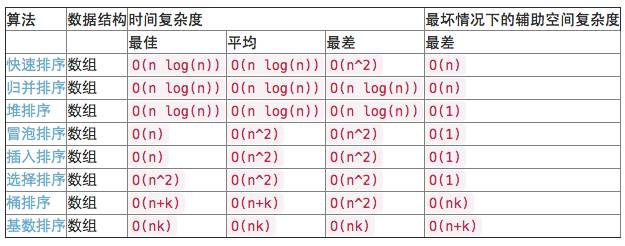
6. 递归 vs. 迭代
对程序员来说,递归应该是一个与生俱来的思想(a built-in thought),可以通过一个简单的例子来说明。
问题: 有n步台阶,一次只能上1步或2步,共有多少种走法。
步骤1:找到走完前n步台阶和前n-1步台阶之间的关系。
为了走完n步台阶,只有两种方法:从n-1步台阶爬1步走到或从n-2步台阶处爬2步走到。如果f(n)是爬到第n步台阶的方法数,那么f(n) = f(n-1) + f(n-2)。
f(0) = 0;f(1) = 1;
步骤2: 确保开始条件是正确的。
publicstaticintf(intn){
if(n<= 2)returnn;
intx=f(n-1)+f(n-2);
returnx;
}
递归方法的时间复杂度是n的指数级,因为有很多冗余的计算,如下:
f(5)
f(4) + f(3)
f(3) + f(2) + f(2) + f(1)
f(2) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
f(1) + f(0) + f(1) + f(1) + f(0) + f(1) + f(0) + f(1)
直接的想法是将递归转换为迭代:
publicstaticintf(intn){
if(n<= 2){
returnn;
}
intfirst=1,second=2;
intthird=0;
for(inti=3;i<= n;i++){
third=first+second;
first=second;
second=third;
}
returnthird;
}
7. 动态规划
动态规划是解决下面这些性质类问题的技术:
一个问题可以通过更小子问题的解决方法来解决(译者注:即问题的最优解包含了其子问题的最优解,也就是最优子结构性质)。
有些子问题的解可能需要计算多次(译者注:也就是子问题重叠性质)。
子问题的解存储在一张表格里,这样每个子问题只用计算一次。
需要额外的空间以节省时间。
爬台阶问题完全符合上面的四条性质,因此可以用动态规划法来解决。
publicstaticint[]A=newint[100];
publicstaticintf3(intn){
if(n<= 2)
A[n]=n;
if(A[n]>0)
returnA[n];
else
A[n]=f3(n-1)+f3(n-2);//store results so only calculate once!
returnA[n];
}
8. 位操作
位操作符:
| 或 | 与 | 亦或 | 左移 | 右移 | 非 |
| 1|0=1 | 1&0=0 | 1^0=1 | 0010<<2=1000 | 1100>>2=0011 | ~1=0 |
获得给定数字n的第i位:( i 从 0 计数,并从右边开始)
publicstaticbooleangetBit(intnum,inti){
intresult=num&(1<
if(result==0){
returnfalse;
}else{
returntrue;
}
例如,获得数字10的第2位:
i=1, n=101<<1= 101010&10=1010 is not 0, so return true;
9. 概率问题
解决概率相关的问题通常需要很好的规划了解问题(formatting the problem),这里刚好有一个这类问题的简单例子:
一个房间里有50个人,那么至少有两个人生日相同的概率是多少?(忽略闰年的事实,也就是一年365天)
计算某些事情的概率很多时候都可以转换成先计算其相对面。在这个例子里,我们可以计算所有人生日都互不相同的概率,也就是:365/365 * 364/365 * 363/365 * ... * (365-49)/365,这样至少两个人生日相同的概率就是1 – 这个值。
publicstaticdoublecaculateProbability(intn){
doublex=1;
for(inti=0;i
x*=(365.0-i)/365.0;
}
doublepro=Math.round((1-x)*100);
returnpro/100;
}
calculateProbability(50) = 0.97
-
算法
+关注
关注
23文章
4646浏览量
93754 -
编程
+关注
关注
88文章
3649浏览量
94359
原文标题:经典:编程面试的 10 大算法概念汇总
文章出处:【微信号:LinuxHub,微信公众号:Linux爱好者】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
关在钉钉和企业微信上使用AI视频面试——AI得贤招聘官操作说明
史上最全面Java面试汇总(面试题+答案)精选资料分享
编程之美--微软技术面试心得





 编程面试的 9 大算法概念
编程面试的 9 大算法概念










评论