低噪放LNA后方的插入损耗对灵敏度有没有影响?
小编为什么问这样的问题,难道没有学噪声级联公式?
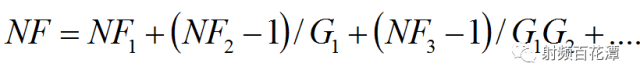
按照以下方式,我在LNA 和IC 之间加个10db 的衰减,对接收灵敏度的影响也很小吗?
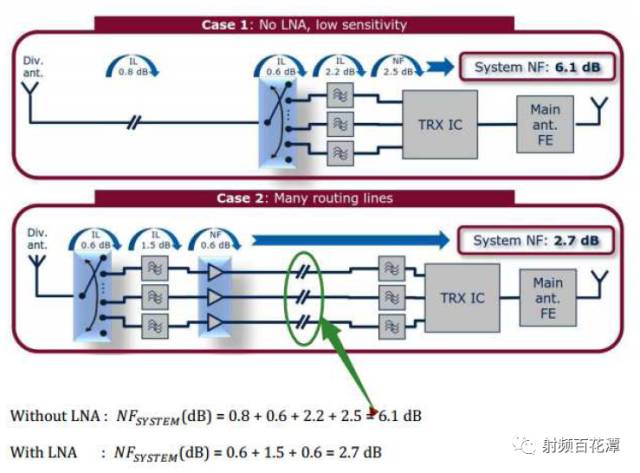
由上面看到了 NFsystem被降低了 6.1-2.7=3.4dB
也就是灵敏度提升了3.4dB
先说结论 要看LNA 后方的Loss 是否远小于LNA 的Gain
Yes => 没影响
No => 有影响
先反问个问题 如果说 LNA 之后的Loss 不影响灵敏度
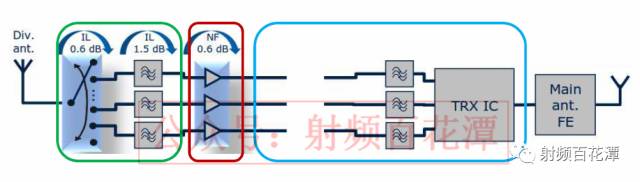
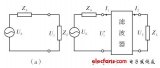
那么 LNA 之后Open(亦即Loss 无限大) 如下图 :
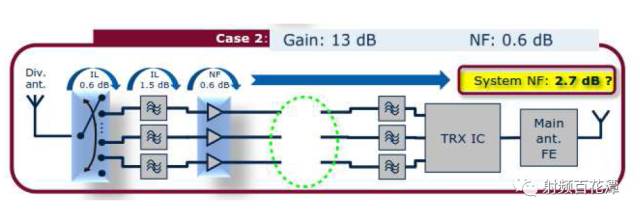
有可能灵敏度不受到影响吗?? 你第一直觉认为不可能
是吧 因为你连讯号都收不到 何来灵敏度??
要探讨LNA 之后的Loss 会不会影响灵敏度
得先知道LNA 之后的Loss 对灵敏度影响程度多大
依据NF级联公式和Friis Formula :
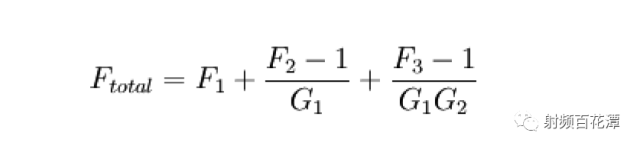
其实计算时 只需以LNA 为分水岭分前后 换言之
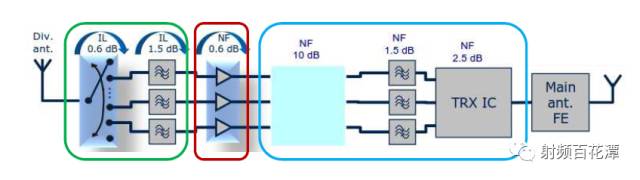
可简化成三个Block 如上图的绿框, 红框, 篮框
计算出来 其NF 为3 dB
而LNA 的Gain 假设为13 dB 也就是G2 要带19.95
你可以发现 当G2 = 19.95 带入分母时 其
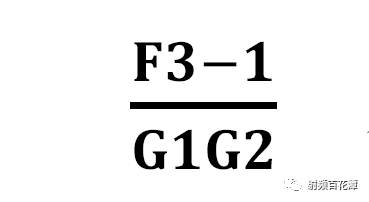
几乎可忽略不计
换言之
LNA 的Gain 会把LNA 后方Block 对接收路径整体NF 的贡献给稀释掉
因此 若我们只计算绿框跟红框的NF 总和 可得到2.7 dB
跟上述计算出来的3 dB 差不多
所以才有『LNA 后方的Loss 可忽略不计』的结论
但是 重点来了
F3-1/G1G2之所以可忽略不计
那是因为 (F3-1)远小于G1G2
以这例子而言
F3-1 = 2
G1G2 = 12.3
F3-1/G1G2= 0.16
反之 如果(F3-1)没有远小于G1G2 则
F3-1/G1G2
就不可忽略不计
以反问那题为例 LNA 之后Open
亦即F3 为无限大,代入Friis Formula :
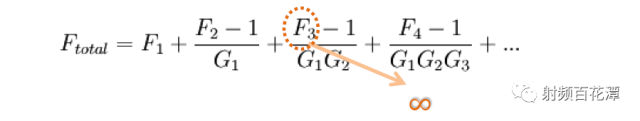
整体接收路径的NF 变成无限大
再根据灵敏度公式 把整体接收路径的NF 无限大 代进公式 :
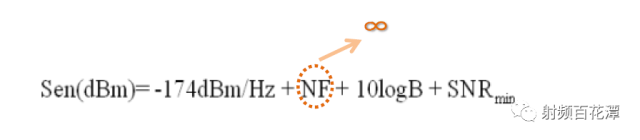
亦即你的灵敏度无限大
这世上不会有无限大的讯号 所以表示你接收机完全收不到讯号
因此 当你(F3-1)没有远小于G1G2 时
LNA 后方的Loss 对灵敏度肯定是有影响
由公式也证实了 你的第一直觉是对的
LNA 之后Open 灵敏度不可能不受到影响
因此回到你一开始的问题
『在LNA 和IC 之间加个10db 的衰减,对接收灵敏度的影响也很小吗?』
我们得计算 加这个10 dB 的衰减后 其(F3-1)有没有远小于G1G2
F3-1 = 24
G1G2 = 12.3
很明显 (F3-1)并没有远小于G1G2
所以这10 dB 衰减 对灵敏度肯定有影响
算出来其整体接收路径的NF 为5.82 dB
而没加这个10 dB 衰减时 刚计算出来的NF 为3 dB
换言之 你加了这个10 dB 衰减后
其灵敏度劣化了 5.82 – 3 = 2.82 dB 所以有影响
当然 你会说 是否LNA 的Gain 越大越好
这样越可以使
『LNA 后方的Loss 远小于LNA 的Gain』这条件成立?
理论上是这样没错
但实际上 LNA 的Gain 若太大
其后方电路会被LNA Output 输出的讯号灌到饱和
其Noise Floor 上升 SNR 下降 那灵敏度还是不会好
况且LNA 的Gain 越大 其整体接收路径的IIP3 就会越小
一旦有两个以上的外来干扰讯号 其产生的IMD3 会越大
因为这IMD3 很靠近RX 讯号 你SAW Filter 也滤不掉
如此一来 IMD3 会让RX 讯号的Noise Floor 上升 SNR 下降
那灵敏度还是不会好
不好的线性度 连带也会产生不好的灵敏度
所以LNA 的Gain 不是越大越好 也不是越小越好 而是刚刚好最好
同时也知道 纵然LNA 可使其后方的Loss 不影响灵敏度
但若其后方的Loss 太大 对于灵敏度 还是会有影响
亦即该LNA 改善灵敏度的程度会大打折扣
-
噪声
+关注
关注
13文章
1114浏览量
47335 -
LNA
+关注
关注
4文章
270浏览量
57329
原文标题:20180319-低噪放LNA后方的插入损耗对灵敏度有没有影响?
文章出处:【微信号:EMC_EMI,微信公众号:电磁兼容EMC】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐
滤波器的通带与插入损耗及频率
插入损耗对差分对的信号质量影响
从多个方面讨论电路的插入损耗,帮助射频工程师理解电路总的插入损耗的来源
利用外部LNA改善接收机灵敏度
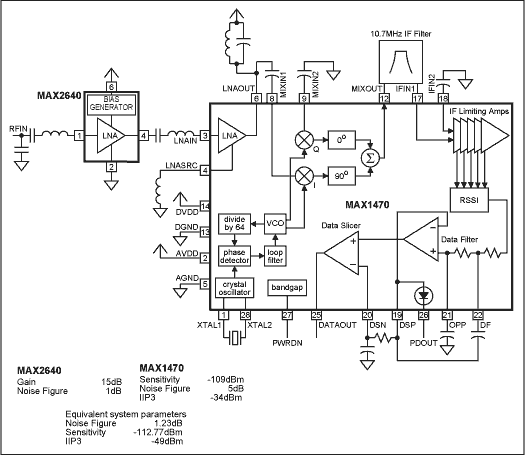
如何用LNA改善GPS的灵敏度
EMI电源滤波器的插入损耗分析




 低噪放LNA后方的插入损耗对灵敏度有没有影响?
低噪放LNA后方的插入损耗对灵敏度有没有影响?











评论