回归样条法介绍及其实现步骤与技巧

作为数据科学领域的新手，你接触的第一个算法是不是线性回归？当你把它用于不同的数据集时，你会发现它非常简单方便，但现实中的很多问题是非线性的，这种依赖因变量和自变量之间线性关系的做法有时行不通。这时，你尝试了多项式回归，虽然大部分时间它给出了更好的结果，但在面对高度可变的数据集时，你的模型也会频繁地过拟合。

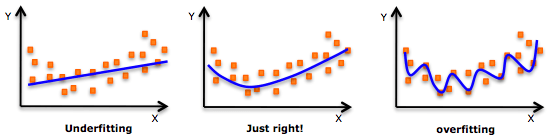
过拟合

我们的模型总是变得太灵活，这对“看不见”的数据来说其实并不合适。你也许听说过加权最小二乘估计（weighted least-squares）、核估计（kernel smoother）、局部多项式估计（local polynomial fitting），但谈到对模型中未知函数的估计，样条估计依然占据着重要的位置。本文将通过一些线性和多项式回归的基础知识，简要介绍样条估计的一种方法——回归样条法（regression spline）以及它的Python实现。

注：本文来自印度数据科学家Gurchetan Singh，假设读者对线性回归和多项式回归有初步了解。

目录

1.了解数据

2.线性回归

3.线性回归改进：多项式回归

4.回归样条法及其实现

分段阶梯函数

基函数

分段多项式

限制和样条

三次样条和自然三次样条

选择结点的数量和位置

回归样条与多项式回归的比较

了解数据

为了理解这些概念，首先我们还是得提一下这本黄黄的、“可爱”的、砖头一样的教材：《统计学习入门》（An Introduction to Statistical Learning with Applications in R）。几天前twitter上有许多人转发了一个段子，说有人在马路边捡到了一本破烂的《统计学习入门》，边上躺着一个空的伏特加酒瓶和空烟盒，这本书的“毒性”请自行体会。

***、酒精以及SVM

书中提到了一个工资预测数据集，感兴趣的读者可以点击这里下载。这个数据集包含诸如身份ID、年份、年龄、性别、婚姻状况、种族、受教育程度、所在地、工作类别、健康状况、保险缴纳和工资等多种信息。为了介绍样条回归，这里我们把“年龄”作为自变量，用它来预测目标的工资情况（因变量）。

先处理数据：

# 导入模块

import pandas as pd

import numpy as np

import statsmodels.api as sm

import matplotlib.pyplot as plt

%matplotlib inline

# 读取data_set

data = pd.read_csv("Wage.csv")

data.head()

data_x = data['age']

data_y = data['wage']

# 将数据分为训练集和测试集

from sklearn.model_selection import train_test_split

train_x, valid_x, train_y, valid_y = train_test_split(data_x, data_y, test_size=0.33, random_state = 1)

# 年龄和工资关系b/w的可视化

import matplotlib.pyplot as plt

plt.scatter(train_x, train_y, facecolor='None', edgecolor='k', alpha=0.3)

plt.show()

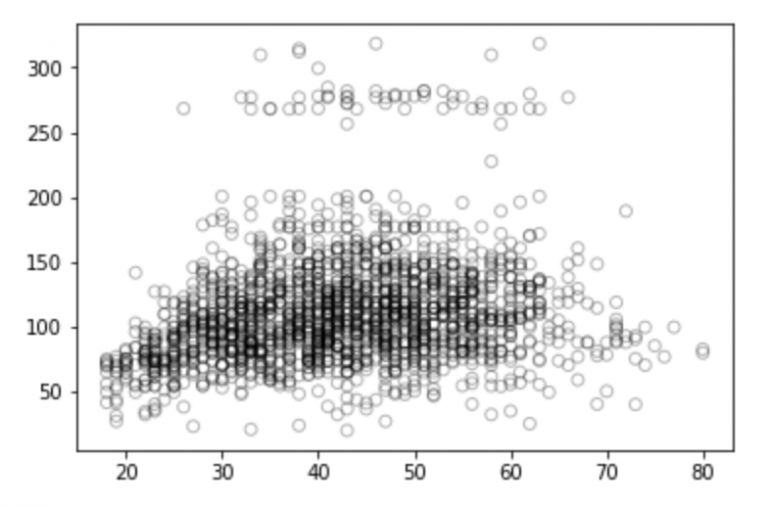
看了这幅图，你对这些离散的点有什么想法吗？它们是积极的、消极的还是全然不相关的？你可以在评论区谈谈自己的想法。但别急，我们先做一些分析。

线性回归

线性回归是一种极其简单的、使用最广泛的用于预测建模的统计方法。作为监督学习算法，它能解决回归问题。当我们建立起因变量和自变量之间的线性关系后，这时我们就得到了一个线性模型。从数学角度看，它可以被当做是一个线性表达式：

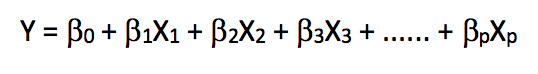
在上式中，Y是因变量，X是自变量，也就是我们常说的特征，β则是分配给特征的权值系数，它们表示各个特征对于最终预测结果的重要性。例如我们设X1对方程结果的影响最大，那么和其他特征相比，β1/权重 的值会大于其他系数和权重的商。

那么，如果我们的线性回归中只有一个特征，这个等式会变成什么样？

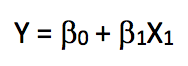
我们把这种只包含一个独立变量的线性回归称为简单线性回归。因为之前的目标是根据“年龄”预测员工的“工资”，所以我们将在训练集上执行简单线性回归，并在测试集上计算模型的误差（均方误差RMSE）。

from sklearn.linear_model importLinearRegression

# Fit线性回归模型

x = train_x.reshape(-1,1)

model = LinearRegression()

model.fit(x,train_y)

print(model.coef_)

print(model.intercept_)

-> array([0.72190831])

-> 80.65287740759283

# 在测试集上预测

valid_x = valid_x.reshape(-1,1)

pred = model.predict(valid_x)

# 可视化

# 我们将从valid_x的最小值和最大值之间选70个plot画图

xp = np.linspace(valid_x.min(),valid_x.max(),70)

xp = xp.reshape(-1,1)

pred_plot = model.predict(xp)

plt.scatter(valid_x, valid_y, facecolor='None', edgecolor='k', alpha=0.3)

plt.plot(xp, pred_plot)

plt.show()

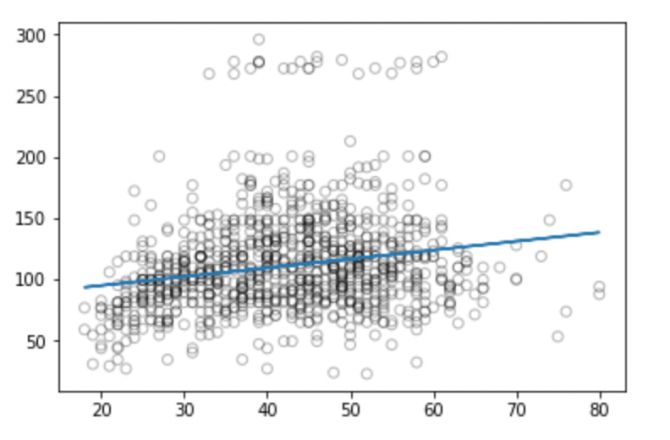
现在我们可以计算模型预测的RMSE：

from sklearn.metrics import mean_squared_error

from math import sqrt

rms = sqrt(mean_squared_error(valid_y, pred))

print(rms)

-> 40.436

从图中我们可以看到，线性回归没法捕捉所有可用的信号，结果不太好。

尽管线性模型的描述和实现相对简单，而且在解释和推理方面也更有优势，但它确实在性能上存在重大限制。线性模型假设各个独立变量之间存在线性关系，可惜的是这总是一个直线拟合的近似值，有时候它的精度会很差。

既然线性模型精度一般，那么我们暂且把线性假设放在一边，在它的基础上进行扩展，比如用多项式回归、阶梯函数等使模型获得性能提升。

线性回归改进：多项式回归

我们先来看看这些可视化图像：

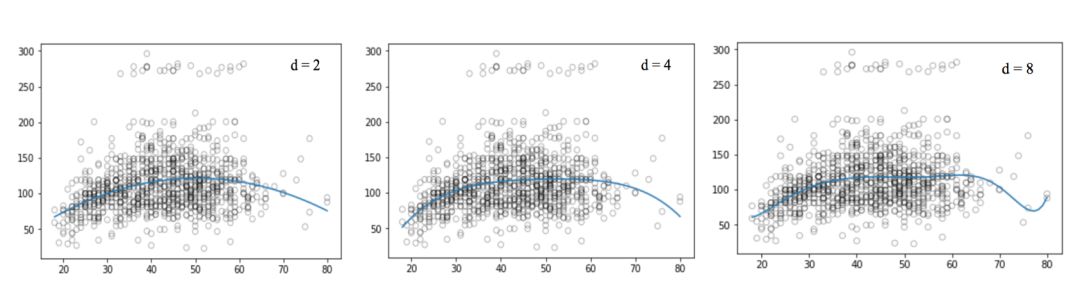
和线性回归那张图相比，上图中的曲线似乎更好地拟合了工资和年龄信号的分布，它们在形状上是非线性的。像这种使用非线性函数的做法，我们称它为多项式回归。

多项式回归通过增加额外预测因子来扩展线性模型，它最直接的做法是在原先的自变量基础上添加乘方运算（幂）。例如一个三次回归会把X1、X22、X33作为自变量。

将线性回归扩展到因变量和自变量之间的非线性关系的一种标准方法是用多项式函数代替线性模型。

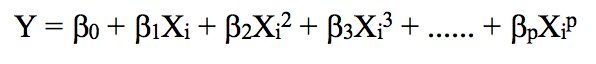
如果我们提高阶值，整个曲线会出现高频震荡，它的后果是模型过拟合。

# 为二次回归函数生成权值，degree =2

weights = np.polyfit(train_x, train_y, 2)

print(weights)

-> array([ -0.05194765, 5.22868974, -10.03406116])

# 用给定的权值生成模型

model = np.poly1d(weights)

# 在测试集上预测

pred = model(valid_x)

# 用70个观察值画图

xp = np.linspace(valid_x.min(),valid_x.max(),70)

pred_plot = model(xp)

plt.scatter(valid_x, valid_y, facecolor='None', edgecolor='k', alpha=0.3)

plt.plot(xp, pred_plot)

plt.show()

同样的，我们可以提高函数的幂（d），看看四次、十二次、十六次、二十五次回归函数的图像：

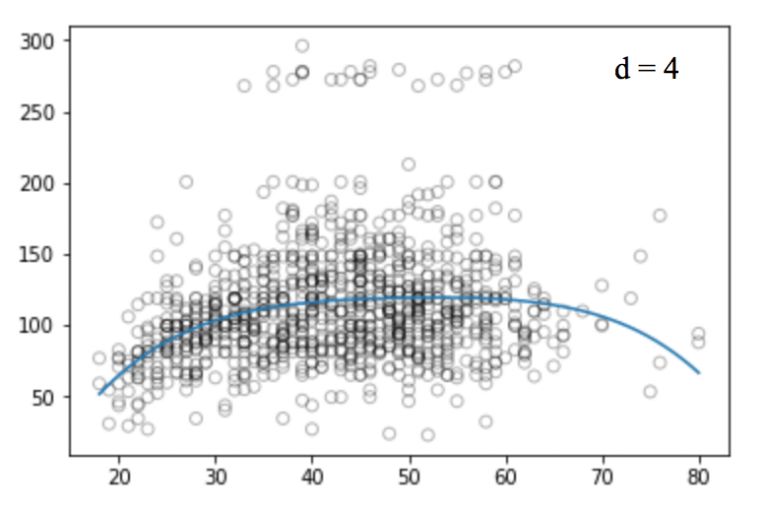
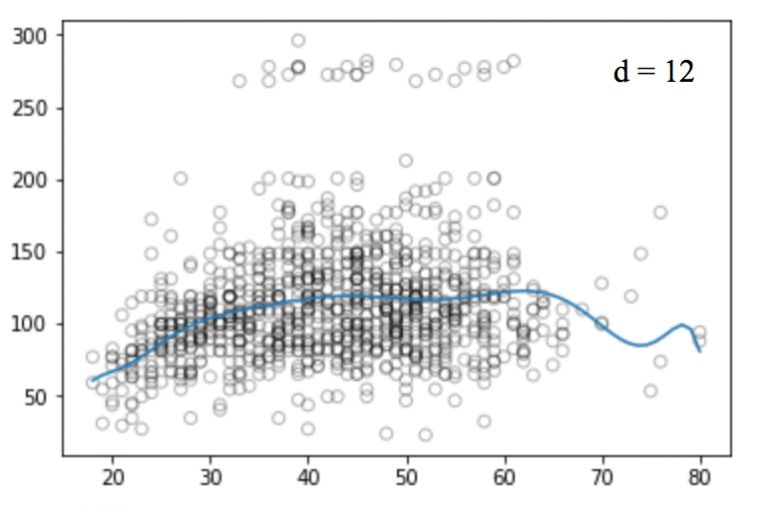
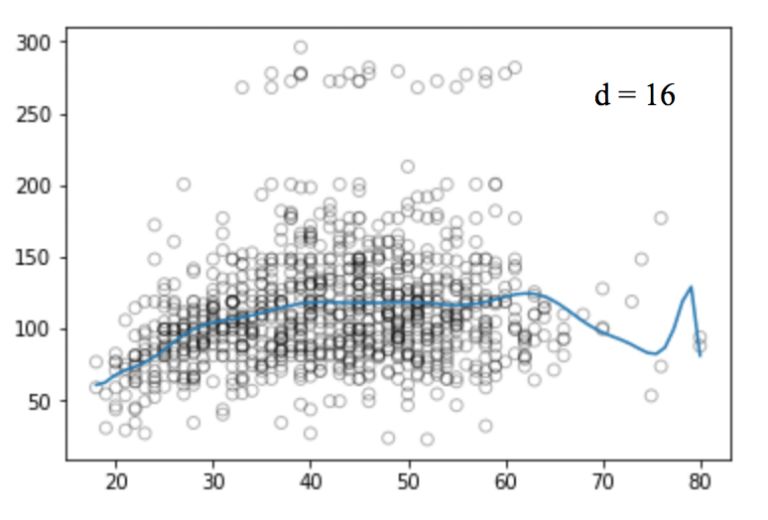
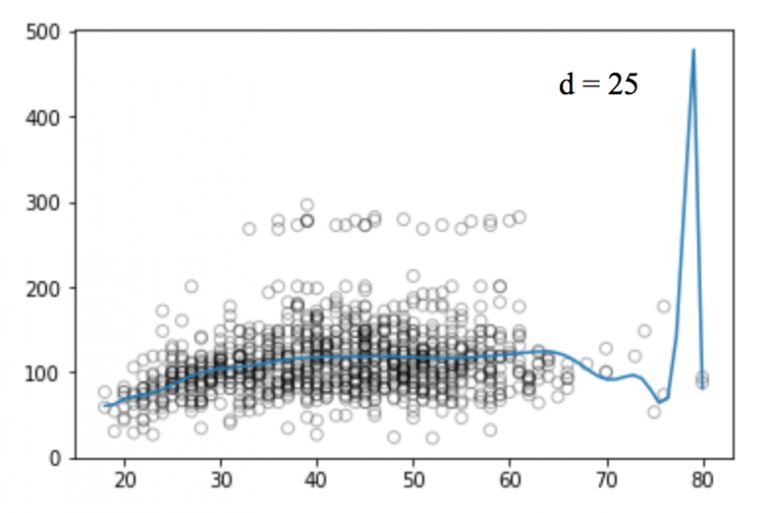
和线性回归一样，多项式回归的缺点也不少。一方面，随着等式变得越来越复杂，函数的数量也会逐渐增加，这就导致我们很难对它们进行处理。另一方面，正如上图所展示的，即便是在这么简单的一维数据集上，幂越高，曲线经过的信号点越多，形状也越诡异，这时模型已经出现过拟合倾向。它并没有从输入和输出中推导出一般规律，而是简单记忆训练集的结果，这样的模型在测试集上不会有良好的性能。

多项式回归还有一些其他的问题，比如它在本质上是非局部的。如果我们改变训练集上一个点的Y值，这会影响多项式对远处某点的拟合情况。因此，为了避免在整个数据集上使用高阶多项式，我们可以用多个不同的低阶多项式函数作为替代。

回归样条法及其实现

为了克服多项式回归的缺点，一种可行的改进方法是不把训练集作为一个整体，而是把它划分成多个连续的区间，并用单独的模型来拟合。这种方法被称为回归样条。

回归样条法是最重要的非线性回归方法之一。在普通多项式回归中，我们通过在现有特征基础上使用多项式函数来生成新特征，对于数据集而言，这些特征具有全局性影响。为了解决这个问题，我们可以把数据分布分成不同的几个部分，然后针对每一部分拟合线性或非线性的低阶多项式函数。

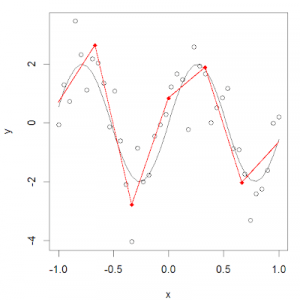
我们把这些分区的红点称为节点（knot），把拟合单个区间数据分布的函数称为分段函数（piecewise function）。如上图所示，这个数据分布可以用多个分段函数来拟合。

分段阶梯函数

阶梯函数是最常见的分段函数之一，它是一个在一定区间内保持不变的函数。通过使用阶梯函数，我们能把X的范围分成几个区间（bin），并在每个区间内拟合不同的常数。

换句话说，假设我们在X范围内设置了K个节点：C1,C2,...,CK，然后构建K+1个新变量：

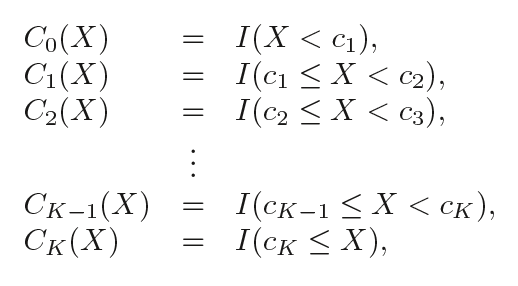
I( )是个指示函数，如果在范围内，即条件为真就返回1；否则返回0。

# 把数据分成4个连续的区间

df_cut, bins = pd.cut(train_x, 4, retbins=True, right=True)

df_cut.value_counts(sort=False)

->

(17.938, 33.5] 504

(33.5, 49.0] 941

(49.0, 64.5] 511

(64.5, 80.0] 54

Name: age, dtype: int64

df_steps = pd.concat([train_x, df_cut, train_y], keys=['age','age_cuts','wage'], axis=1)

# 为年龄组创建虚拟变量

df_steps_dummies = pd.get_dummies(df_cut)

df_steps_dummies.head()

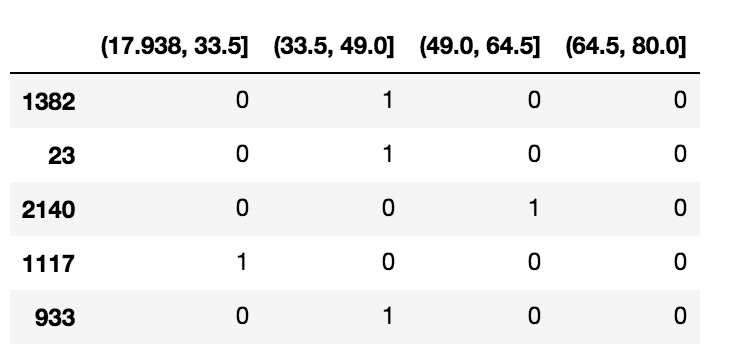
df_steps_dummies.columns = ['17.938-33.5','33.5-49','49-64.5','64.5-80']

# 拟合广义线性模型

fit3 = sm.GLM(df_steps.wage, df_steps_dummies).fit()

# 把分段函数对应到相应的4个区间内

bin_mapping = np.digitize(valid_x, bins)

X_valid = pd.get_dummies(bin_mapping)

# 删除异常值

X_valid = pd.get_dummies(bin_mapping).drop([5], axis=1)

# 预测

pred2 = fit3.predict(X_valid)

# 计算RMSE

from sklearn.metrics import mean_squared_error

from math import sqrt

rms = sqrt(mean_squared_error(valid_y, pred2))

print(rms)

->39.9

# 用70个观察值画图

xp = np.linspace(valid_x.min(),valid_x.max()-1,70)

bin_mapping = np.digitize(xp, bins)

X_valid_2 = pd.get_dummies(bin_mapping)

pred2 = fit3.predict(X_valid_2)

# 可视化

fig, (ax1) = plt.subplots(1,1, figsize=(12,5))

fig.suptitle('Piecewise Constant', fontsize=14)

# 多项式回归线散点图

ax1.scatter(train_x, train_y, facecolor='None', edgecolor='k', alpha=0.3)

ax1.plot(xp, pred2, c='b')

ax1.set_xlabel('age')

ax1.set_ylabel('wage')

plt.show()

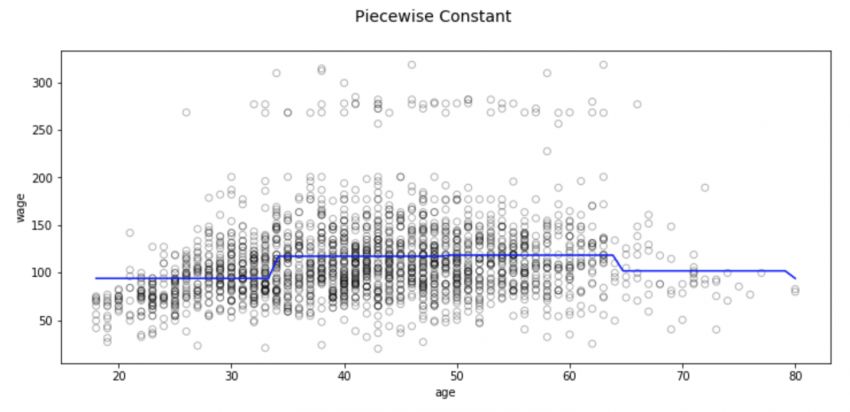
这种分区方法也存在一些问题，其中最显著的是我们期望输入不同，模型的输出也会发生相应变化。但分类回归不会创建预测变量的连续函数，因此在大多数情况下，其实它的假设是输入和输出之间没有关系。例如在上图中，第一个区间的函数显然没有发现到随年龄增长工资也会不断上涨的趋势。

基函数

为了捕捉回归模型中的非线性因素，我们需要对一部分甚至所有的预测变量做一些变换。我们希望这是一个非常普遍的变换，它既能避免模型把每个自变量看作线性的，可以灵活地拟合各种形状的数据分布，又相对的不那么“灵活”，能有效防止过拟合。

像这种可以组合在一起以捕捉数据分布情况的变换，我们称之为基函数，也称样条基。在根据年龄预测工资的这个问题中，样条基为b1(X), b2(X),…,bK(X)。

现在，我们不再用X拟合线性模型，而是用这个新模型：

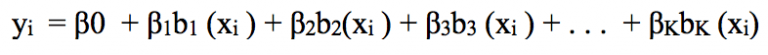
让我们深入了解基函数的一种基础用法：分段多项式。

分段多项式

在介绍分段阶梯函数时，我们介绍它是“把X分成几个区间，并在每个区间内拟合不同的常数”，套用线性回归和多项式回归的区别，分段多项式则是把X分成几个区间，并在每个区间内拟合不同的低阶多项式函数。由于函数的幂较低，所以图像不会剧烈震荡。

例如，分段二次多项式可以通过拟合二元回归方程来发挥作用：

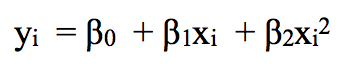
其中β0、β1和β2在不同区间内取值不同。详细来说，如果我们有一个包含单个节点c的数据集，那它的分段三次多项式应该具有以下形式：

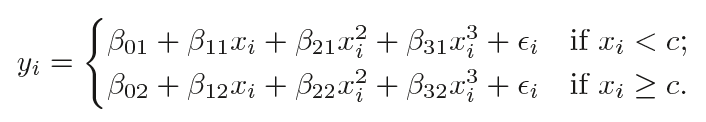
这其实是拟合了两个不同的多项式函数：一个xi

需要注意的一点是，这个多项式函数共有8个变量，每个多项式4个。

节点越多，分段多项式就越灵活，因为我们要为每个X区间分配不同的函数，而函数的形式则取决于该区间的数据分布。一般来说，如果我们在整个X范围内设置了K个不同的节点，我们最终将拟合K+1个不同的三次多项式。理论上来说，我们可以用任意低阶多项式拟合某个单独区间。

现在我们来看看设计分段多项式时应遵循的一些必要条件和限制条件。

约束和样条

能拟合目标区间数据分布的函数有很多，但分段多项式是不能随便设的，它也有各种需要遵循的限制条件。我们先来看看这幅图：

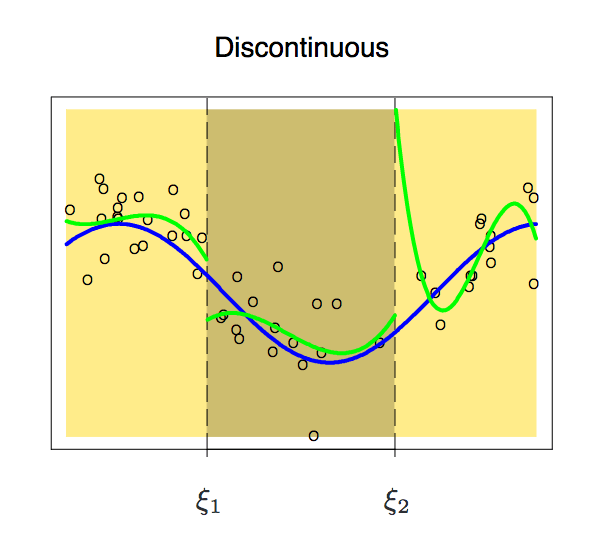
因为是分段的，两个区间的函数可能会出现不连续的现象。为了避免这种情况，一个必要的额外限制就是任一侧的多项式在节点上应该是连续的。

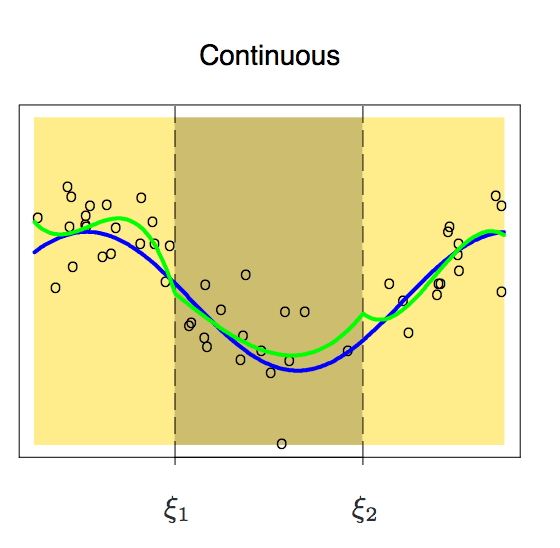
增加了这个约束条件后，我们得到了一条连续的曲线，但它看起来完美吗？答案显然是否定的，在阅读下文之前，我们可以先自行思考一个问题，为什么我们不能接受这种不流畅的曲线？

根据上图可以发现，这时节点在曲线上还很突出，为了平滑节点上的多项式，我们需要增加一个新约束：两个多项式的一阶导数必须相同。这里有一点值得注意，我们每增加一个条件，多项式就有效释放一个自由度，这可以降低分段多项式拟合的复杂性。因此在上图中，我们只用了10个自由度而不是12个。

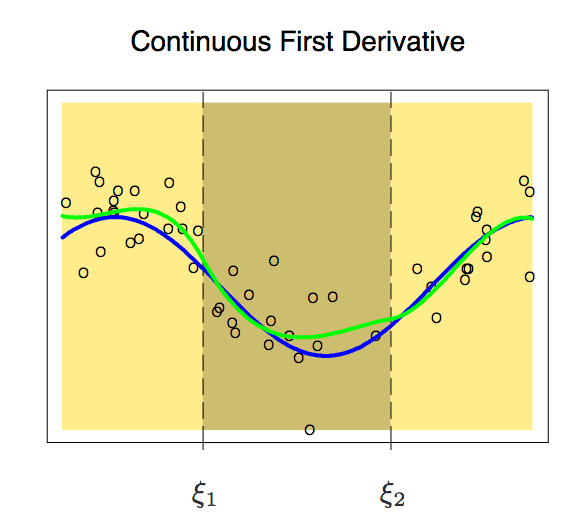
加入一阶导数后，现在我们的多项式稍稍变得平滑了一些。这时它的自由度也从12个减少到了8个。虽然曲线改进了不少，但它还有不少提升空间。所以现在，我们再向它施加一个新约束：一个节点上两个多项式的二阶导数必须相同。

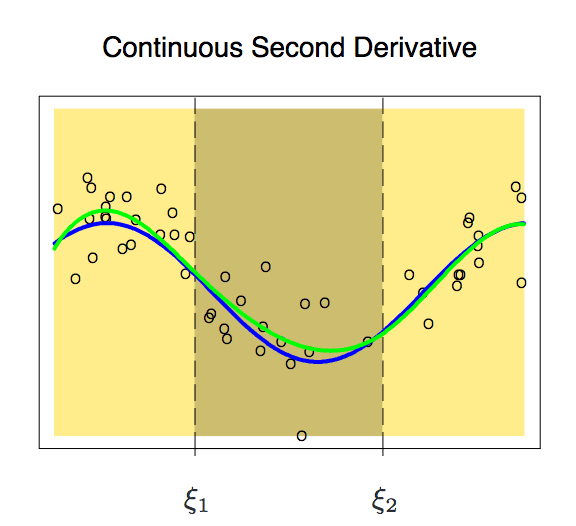
这条曲线就比较符合我们预期了，它只有6个自由度。像这样具有m-1个连续导数的m阶分段多项式，我们称之为样条（Spline）。

三次样条和自然三次样条

三次样条指的是具有一组约束（连续性、一阶和二阶连续性）的分段多项式。通常情况下，具有K个节点的三次样条一般有(K+1)×4-K×3，也就是K+4个维度。当K=3时，维度为8，这时图像的自由度是维度-1=7。一般情况下，我们只用三次样条。

from patsy import dmatrix

import statsmodels.api as sm

import statsmodels.formula.api as smf

# 在25、40和60三个节点生成三次样条

transformed_x = dmatrix("bs(train, knots=(25,40,60), degree=3, include_intercept=False)", {"train": train_x},return_type='dataframe')

# 在分区的数据集上拟合广义线性模型

fit1 = sm.GLM(train_y, transformed_x).fit()

# 生成4节三次样条曲线

transformed_x2 = dmatrix("bs(train, knots=(25,40,50,65),degree =3, include_intercept=False)", {"train": train_x}, return_type='dataframe')

# 在分区的数据集上拟合广义线性模型

fit2 = sm.GLM(train_y, transformed_x2).fit()

# 两个样条同时预测

pred1 = fit1.predict(dmatrix("bs(valid, knots=(25,40,60), include_intercept=False)", {"valid": valid_x}, return_type='dataframe'))

pred2 = fit2.predict(dmatrix("bs(valid, knots=(25,40,50,65),degree =3, include_intercept=False)", {"valid": valid_x}, return_type='dataframe'))

# 计算RMSE

rms1 = sqrt(mean_squared_error(valid_y, pred1))

print(rms1)

-> 39.4

rms2 = sqrt(mean_squared_error(valid_y, pred2))

print(rms2)

-> 39.3

# 用70个观察值画图

xp = np.linspace(valid_x.min(),valid_x.max(),70)

# 预测

pred1 = fit1.predict(dmatrix("bs(xp, knots=(25,40,60), include_intercept=False)", {"xp": xp}, return_type='dataframe'))

pred2 = fit2.predict(dmatrix("bs(xp, knots=(25,40,50,65),degree =3, include_intercept=False)", {"xp": xp}, return_type='dataframe'))

# 绘制样条曲线和误差曲线

plt.scatter(data.age, data.wage, facecolor='None', edgecolor='k', alpha=0.1)

plt.plot(xp, pred1, label='Specifying degree =3 with 3 knots')

plt.plot(xp, pred2, color='r', label='Specifying degree =3 with 4 knots')

plt.legend()

plt.xlim(15,85)

plt.ylim(0,350)

plt.xlabel('age')

plt.ylabel('wage')

plt.show()

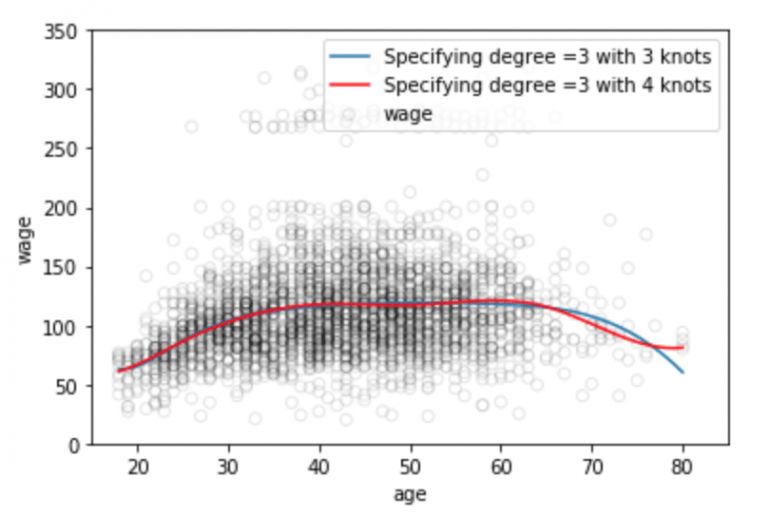
众所周知，拟合数据分布的多项式函数在数据边界地带往往是不稳定的，边界区域的已知数据少，函数曲线常常会过拟合，这个问题同样存在于样条中。为了使多项式更平滑地扩展到边界节点之外，我们需要用到一种叫做自然样条的特殊方法。

相比三次样条，自然三次样条在边界区域增加了一个线性约束。这里我们说明一下，边界区域指的是自变量X的最大值/最小值与相应的最大最小节点之间的区域，这里信号比较稀疏，用线性处理简单控制RMSE值是可以接受的。这时函数的三阶、二阶就成了0，每个减少2个自由度，而这些自由度又在每条曲线的两段，所以多项式的维度K+4个维度这时就变成了K。

# 生成自然三次样条

transformed_x3 = dmatrix("cr(train,df = 3)", {"train": train_x}, return_type='dataframe')

fit3 = sm.GLM(train_y, transformed_x3).fit()

# 在测试集上预测

pred3 = fit3.predict(dmatrix("cr(valid, df=3)", {"valid": valid_x}, return_type='dataframe'))

# Calculating RMSE value

rms = sqrt(mean_squared_error(valid_y, pred3))

print(rms)

-> 39.44

# 用70个观察值画图

xp = np.linspace(valid_x.min(),valid_x.max(),70)

pred3 = fit3.predict(dmatrix("cr(xp, df=3)", {"xp": xp}, return_type='dataframe'))

# 绘制样条曲线

plt.scatter(data.age, data.wage, facecolor='None', edgecolor='k', alpha=0.1)

plt.plot(xp, pred3,color='g', label='Natural spline')

plt.legend()

plt.xlim(15,85)

plt.ylim(0,350)

plt.xlabel('age')

plt.ylabel('wage')

plt.show()

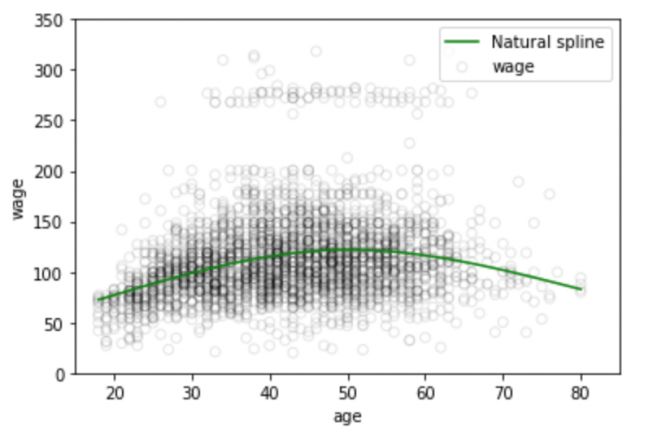
结点的数量和位置

说了这么多，那么当我们拟合样条时，我们该怎么选择节点？一种可行的方法是选择数据分布中的剧烈变化区域作为节点，如经济现象中的突变时刻——金融危机；第二种方法则是在数据变化复杂的地方多设置节点，在看起来更稳定的地方少设置节点，虽然这样做能起作用，但一般我们为了简便还是会截取长度相同的区间。另外，平均分配相同样本点个数是第三种常用的方法。

这里我们简要介绍第四种更客观的做法——交叉验证。要用这种方法，我们需要：

取走一部分数据；

用一定数量的节点使样条拟合剩下的这些数据；

用样条拟合之前取走的数据。

我们重复这个过程，直到每个观察值被忽略1次，再计算整个交叉验证的RMSE。它可以针对不同数量的节点重复多次，最后选择输出最小RMSE的K值。

回归样条与多项式回归的比较

回归样条一般能比多项式回归得到更好的输出。因为它与多项式不同，多项式必须要用高次多项式灵活地拟合整个数据集，而回归样条在保留非线性函数的灵活性的同时，依靠节点保证了整体的稳定性。

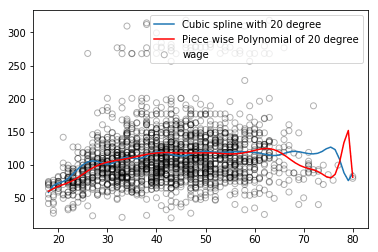
如上图所示，蓝色的回归样条曲线整体更平滑，捕捉到的信息也更全面。稳定只是一方面，此外，回归样条可以通过控制节点数量调节样条的灵活性，同时它也能添加线性约束来控制曲线在边界区域的结果，这使它能更有效地防止过拟合。

小结

写到这里，本文已接近尾声。通过这篇文章，我们了解了回归样条及其相较于线性回归和多项式回归的优势。在《统计学习入门》中，你还可以进一步学习另一种适用于高度可变数据集的生成样条方法，称为平滑样条。它与Ridge/Lasso正则化类似，惩罚了损失函数和平滑函数。