神经元和神经网络层的标准C++定义

前一段时间做了一个数字识别的小系统，基于BP神经网络算法的，用MFC做的交互。在实现过程中也试着去找一些源码，总体上来讲，这些源码的可移植性都不好，多数将交互部分和核心算法代码杂糅在一起，这样不仅代码阅读困难，而且重要的是核心算法不具备可移植性。设计模式，设计模式的重要性啊！于是自己将BP神经网络的核心算法用标准C++实现，这样可移植性就有保证的，然后在核心算法上实现基于不同GUI库的交互（MFC，QT）是能很快的搭建好系统的。下面边介绍BP算法的原理（请看《数字图像处理与机器视觉》非常适合做工程的伙伴），边给出代码的实现，最后给出基于核心算法构建交互的例子。

人工神经网络的理论基础

1.感知器

感知器是一种具有简单的两种输出的人工神经元，如下图所示。

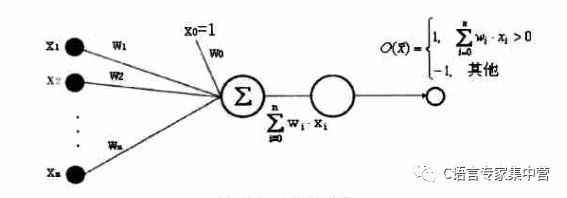
2.线性单元

只有1和-1两种输出的感知器实际上限制了其处理和分类的能力，下图是一种简单的推广，即不带阈值的感知器。

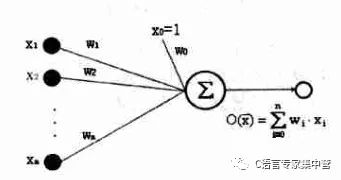
3.误差准则

使用的是一个常用的误差度量标准，平方误差准则。公式如下。

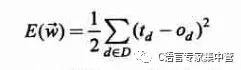
其中D为训练样本，td为训练观测值d的训练输出，ot为观测值d的实际观测值。如果是个凸函数就好了（搞数学的，一听到凸函数就很高兴，呵呵！），但还是可以用梯度下降的方法求其参数w。

4.梯度下降推导

在高等数学中梯度的概念实际上就是一个方向向量，也就是方向导数最大的方向，也就是说沿着这个方向，函数值的变化速度最快。我们这里是做梯度下降，那么就是沿着梯度的负方向更新参数w的值来快速达到E函数值的最小了。这样梯度下降算法的步骤基本如下：

1）初始化参数w（随机，或其它方法）。

2）求梯度。

3）沿梯度方向更新参数w，可以添加一个学习率，也就是按多大的步子下降。

4）重复1），2），3）直到达到设置的条件（迭代次数，或者E的减小量小于某个阈值）。

梯度的表达式如下：

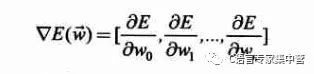
那么如何求梯度呢？就是复合函数求导的过程，如下：

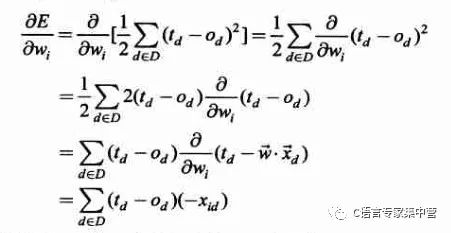
其中xid为样本中第d个观测值对应的一个输入分量xi。这样，训练过程中参数w的更新表达式如下（其中添加了一个学习率，也就是下降的步长）：

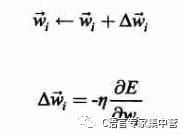
于是参数wi的更新增量为：

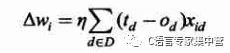
对于学习率选择的问题，一般较小是能够保证收敛的，看下图吧。

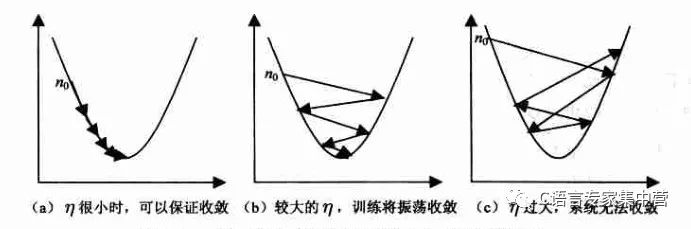
5.增量梯度下降

对于4中的梯度下降算法，其缺点是有时收敛速度慢，如果在误差曲面上存在多个局部极小值，算法不能保证能够找到全局极小值。为了改善这些缺点，提出了增量梯度下降算法。增量梯度下降，与4中的梯度下降的不同之处在于，4中对参数w的更新是根据整个样本中的观测值的误差来计算的，而增量梯度下降算法是根据样本中单个观测值的误差来计算w的更新。

6.梯度检验

这是一个比较实用的内容，如何确定自己的代码就一定没有错呢？因为在求梯度的时候是很容易犯错误的，我就犯过了，嗨，调了两天才找出来，一个数组下表写错了，要是早一点看看斯坦福大学的深度学习基础教程就好了，这里只是截图一部分，有时间去仔细看看吧。

多层神经网络

好了有了前面的基础，我们现在就可以进行实战了，构造多层神经网络。

1.Sigmoid神经元

Sigmoid神经元可由下图表示：

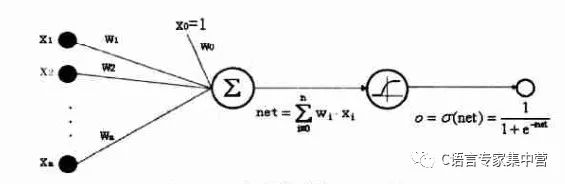
2.神经网络层

一个三层的BP神经网络可由下图表示：

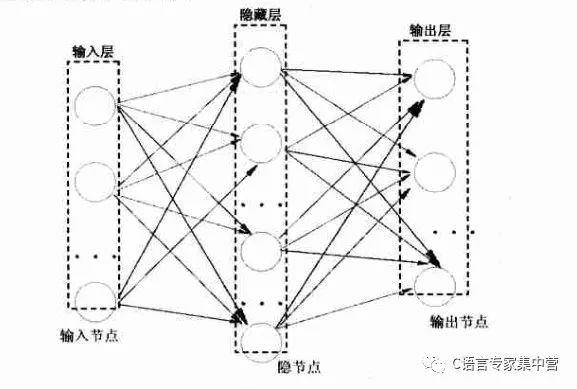
3.神经元和神经网络层的标准C++定义

由2中的三层BP神经网络的示意图中可以看出，隐藏层和输出层是具有类似的结构的。神经元和神经网络层的定义如下：

1