一文看懂无码间串扰的条件

无码间串扰的条件

无码间串扰的条件只要基带传输系统的冲激响应波形h（t）仅在本码元的抽样时刻上有最大值，并在其他码元的抽样时刻上均为0，则可消除码间串扰。即，若对h（t）在时刻t=kTs（这里假设信道和接收滤波器所造成的延迟t0=0）抽样，则应有下式成立：

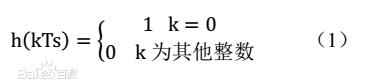
上式（1）称为无码间串扰的时域条件。即，若h（t）的抽样值除了在t=0时不为零外，在其他所有抽样点上均为零，就不存在码间串扰。

无码间串扰的传输特性的设计

1、理想低通特性

满足奈奎斯特第一准则的有很多种，一种极限情况，就是为理想低通型，即

当h（t）等于正负kTs（k不等于0）时有周期性零点，当发送序列的时间间隔为Ts时，正好巧妙地利用了这些零点，只要接收端在t=kTs时间点上抽样，就能实现无码间串扰。

令人遗憾的是，虽然理想低通传输特性达到了基带系统的极限传输速率和极限频带利用率，可是这种特性在物理上是无法实现的。而且，它的冲激响应h（t）作为传输波形仍然是不适宜的。

2、余弦滚降特性

为了解决理想低通特性存在的问题，可以使理想低通滤波器特性的边沿缓慢下降，这称为滚降。只要H（w）在滚降段中心频率处呈奇对称的振幅特性，就必然可以满足奈奎斯特第一准则，从而实现无码间串扰传输。这种设计也可看成是理想特性以奈奎斯特带宽为中心按奇对称条件进行滚降的结果。设计的关键参数是滚降系数。

这种系统所占的频带宽，是理想低通系统的2倍。

验证无码间串扰的条件

利用matlab仿真，验证无码间串扰的条件，画出相关波形及眼图，并画出有噪声时的误码率特性曲线

基本原理

1、码间串扰简介

传输数字信号，会引起相邻数字信号波形之间在时间上的相互重叠，即所谓的码间串扰，由于码间串扰的存在，在接收端译码判决时就会可能引起错误。另外课本中给出了无码间串扰的条件，即奈奎斯特第一准则，通过本实验加深对码间串扰和奈奎斯特第一准则的理解。

2、眼图简介

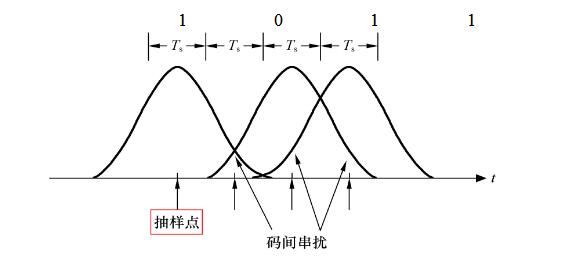
为了衡量基带传输系统性能的优劣，通常用示波器观察接收信号波形的方法，来分析码间串扰和噪声的影响，这就是眼图分析法，如下图所示。

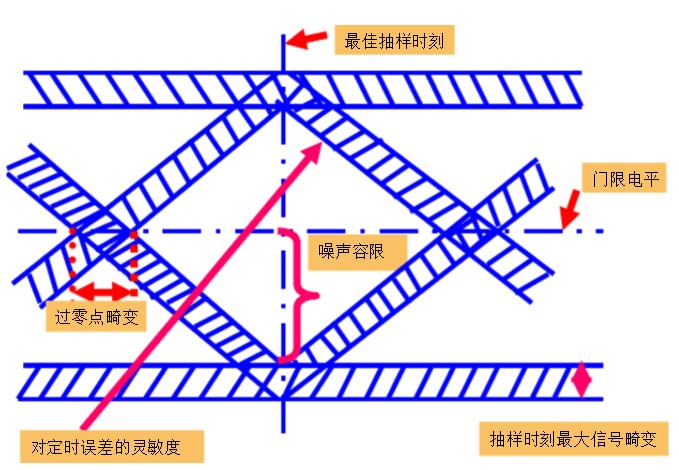
信号失真较小时：眼图为大眼睛，单眼皮；

信号失真较大时：眼图为小眼睛，多眼皮。

仿真结果与分析

程序运行结果：

1、通过升余弦基带传输系统前的抽样点实际值曲线

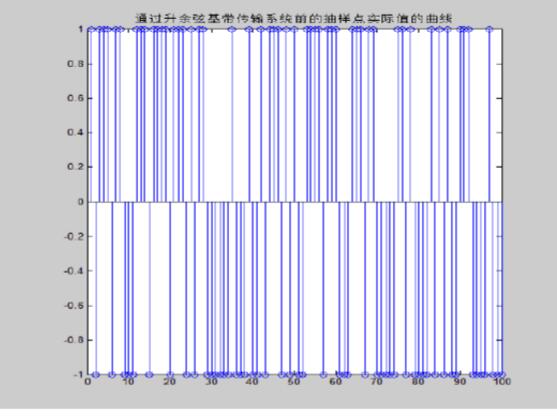
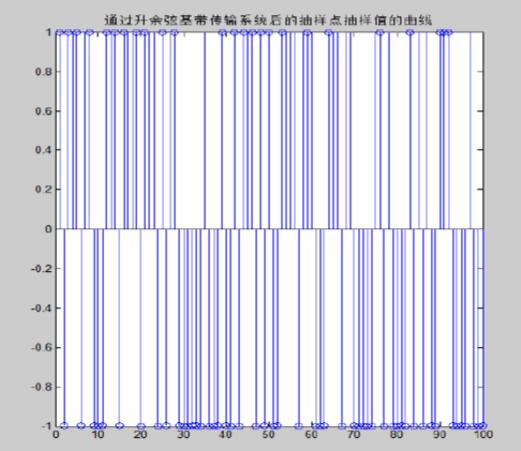
2、眼图

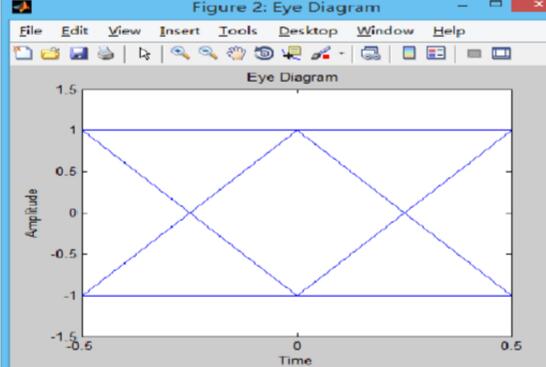
3、误码率曲线

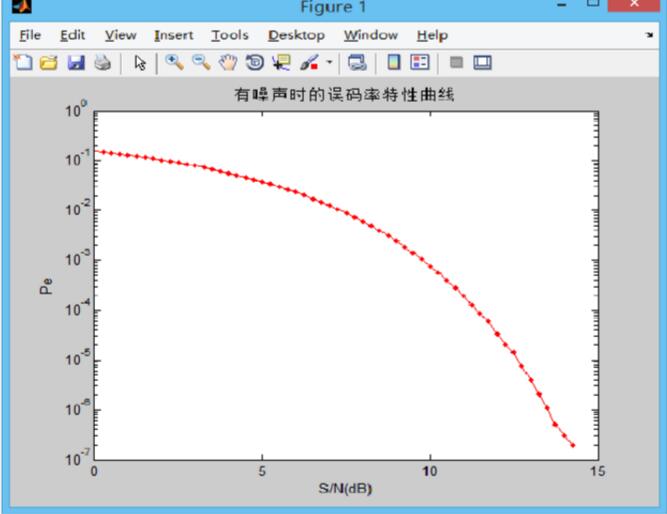
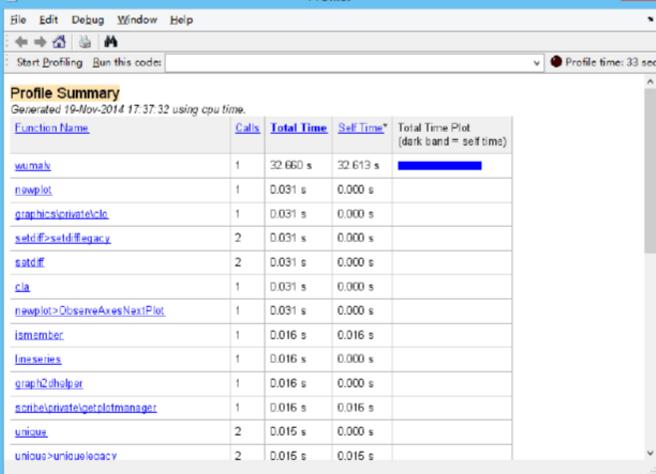
以上四个图分些为通过升余弦基带传输系统前的抽样点实际值曲线通过升余弦基带传输系统前的抽样点实际值曲线，眼图及误码率曲线，图五显示了程序运行的相关信息。从误码率曲线可以发现在一定范围内，当信噪比越大，对应的信道传输的误码率越小。