最优化是指由变量x构成的目标函数f(x)进行最小化或最大化的过程。在机器学习或深度学习术语中,通常指最小化损失函数J(w),其中模型参数w∈R^d。最小化最优化算法具有以下的目标:
- 如果目标函数是凸的,那么任何的局部最小值都是全局最小值。
- 通常情况下,在大多数深度学习问题中,目标函数是非凸的,那就只能找到目标函数邻域内的最低值。
图1: 向着最小化迈进
目前主要有三种最优化算法:
- 对单点问题,最优化算法不用进行迭代和简单求解。
- 对于逻辑回归中经常用到梯度下降法,这类最优化算法本质上是迭代,不管参数初始化好坏都能收敛到可接受的解。
- 对于一系列具有非凸损失函数的问题中,如神经网络。为保证收敛速度与低错误率,最优化算法中的参数初始化中起着至关重要的作用。
梯度下降是机器学习和深度学习中最常用的优化算法。它属于一阶优化算法,参数更新时只考虑一阶导数。在每次迭代中,梯度表示最陡的上升方向,于是我们朝着目标函数梯度的反方向更新参数,并通过学习速率α来调整每次迭代中达到局部最小值的步长。因此,目标函数会沿着下坡的方向,直到达到局部最小值。
在本文中,我们将介绍梯度下降算法及其变种:批量梯度下降,小批量梯度下降和随机梯度下降。
我们先看看梯度下降是如何在逻辑回归中发挥作用的,然后再讨论其它变种算法。简单起见,我们假设逻辑回归模型只有两个参数:权重w和偏差b。
1.将初始化权重w和偏差b设为任意随机数。
2.为学习率α选择一个合适的值,学习速率决定了每次迭代的步长。
- 如果α非常小,则需要很长时间才能收敛并且计算量很大。
- 如果α较大,则可能无法收敛甚至超出最小值。
- 通过我们会使用以下值作为学习速度 : 0.001, 0.003, 0.01, 0.03, 0.1, 0.3.

图2: 不同学习速度下的梯度下降
因此,通过观察比较不同的α值对应的损失函数变化,我们选择第一次未达到收敛的α值的前一个作为最终的α值,这样我们就可以有一个快速且收敛的学习算法。
3.如果数据尺度不一,那就要对数据进行尺度缩放。如果我们不缩放数据,那么等高线(轮廓)会变得越来越窄,意味着它需要更长的时间来达到收敛(见图3)。

图3. 梯度下降: 数据归一化后的等高线与未进行归一化的对比
使数据分布满足μ= 0和σ= 1。以下是数据缩放的公式:

4.在每次迭代中,用损失函数J的偏导数来表示每个参数(梯度)

更新方程如下:

- 特地说明一下,此处我们假设不存在偏差。 如果当前值w对应的梯度方向为正,这意味着当前点处在最优值w*的右侧,则需要朝着负方向更新,从而接近最优值w*。然而如果现在梯度是负值,那么更新方向将是正的,将增加w的当前值以收敛到w*的最优值(参见图4):
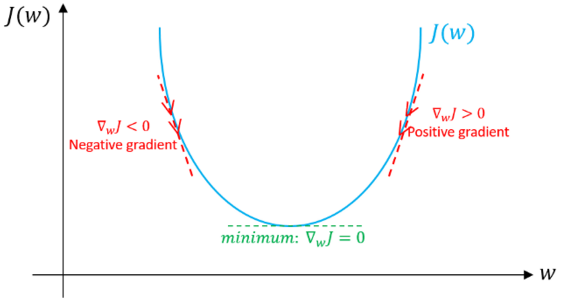
图4: 梯度下降,示例说明梯度下降算法如何用损失函数的一阶导数实现下降并达到最小值。
- 继续这个过程,直至损失函数收敛。也就是说,直到误差曲线变得平坦不变。
- 此外,每次迭代中,朝着变化最大的方向进行,每一步都与等高线垂直。
上面就是梯度下降法的一般过程,我们需要确定目标函数、优化方法,并通过梯度来引导系统搜寻到最优值。
现在我们来讨论梯度下降算法的三个变种,它们之间的主要区别在于每个学习步骤中计算梯度时使用的数据量,是对每个参数更新(学习步骤)时的梯度准确性与时间复杂度的折衷考虑。
批量梯度下降
批量梯度下降是指在对参数执行更新时,在每次迭代中使用所有的样本。

for i in range(num_epochs):
grad = compute_gradient(data, params)
params = params — learning_rate * grad
主要的优点:
- 训练期间,我们可以使用固定的学习率,而不用考虑学习率衰减的问题。
- 它具有朝向最小值的直线轨迹,并且如果损失函数是凸的,则保证理论上收敛到全局最小值,如果损失函数不是凸的,则收敛到局部最小值。
- 梯度是无偏估计的。样本越多,标准误差就越低。
主要的缺点:
- 尽管我们可以用向量的方式计算,但是可能仍然会很慢地遍历所有样本,特别是数据集很大的时候算法的耗时将成为严重的问题。
- 学习的每一步都要遍历所有样本,这里面一些样本可能是多余的,并且对更新没有多大贡献。
小批量梯度下降
为了克服上述方法的缺点,人们提出了小批量梯度下降。在更新每一参数时,不用遍历所有的样本,而只使用一部分样本来进行更新。 因此,每次只用小批量的b个样本进行更新学习,其主要过程如下:

- 打乱训练数据集以避免样本预先存在顺序结构。
- 根据批量的规模将训练数据集分为b个小批量。如果训练集大小不能被批量大小整除,则将剩余的部分单独作为一个小批量。
for i in range(num_epochs):
np.random.shuffle(data)
for batch in radom_minibatches(data, batch_size=32):
grad = compute_gradient(batch, params)
params = params — learning_rate * grad
批量的大小我们可以调整,通常被选为2的幂次方,例如32,64,128,256,512等。其背后的原因是一些像GPU这样的硬件也是以2的幂次方的批量大小来获得更好的运行时间。
主要的优点:
- 比起批量梯度下降,速度更快,因为它少用了很多样本。
- 随机选择样本有助于避免对学习没有多大贡献冗余样本或非常相似的样本的干扰。
- 当批量的大小小于训练集大小时,会增加学习过程中的噪声,有助于改善泛化误差。
- 尽管用更多的样本可以获得更低的估计标准误差,但所带来的计算负担却小于线性增长
主要缺点:
- 在每次迭代中,学习步骤可能会由于噪声而来回移动。 因此它会在最小值区域周围波动,但不收敛。
- 由于噪声的原因,学习步骤会有更多的振荡(见图4),并且随着我们越来越接近最小值,需要增加学习衰减来降低学习速率。

图5: 梯度下降:批量与小批量的损失函数对比
对于大规模的训练数据集,我们通常不需要超过2-10次就能遍历所有的训练样本。 注意:当批量大小b等于训练样本数m时候,这种方法就相当于批量梯度下降。
随机梯度下降
随机梯度下降(SGD)只对样本(xi,yi)执行参数更新,而不是遍历所有样本。因此,学习发生在每个样本上,其具体过程如下:
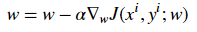
- 打乱训练数据集以避免样本预先存在顺序
- 将训练数据集划分为m个样本。
for i in range(num_epochs):
np.random.shuffle(data)
for example in data:
grad = compute_gradient(example, params)
params = params — learning_rate * grad
它与小批量版本拥有很多相似的优点和缺点。以下是特定于SGD的特性:
- 与小批量方法相比,它为学习过程增加了更多的噪声,有助于改善泛化误差。但同时也增加了运行时间。
- 我们不能用向量的形式来处理1个样本,导致速度非常慢。 此外,由于每个学习步骤我们仅使用1个样本,所以方差会变大。
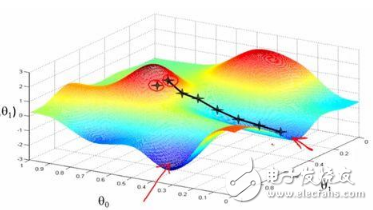
下图显示了梯度下降的变种方法以及它们朝向最小值的方向走势,如图所示,与小批量版本相比,SGD的方向噪声很大:

图6: 梯度下降变种方法朝向最小值的轨迹
难点
以下是关于梯度下降算法及其变种遇到的一些常见问题:
- 梯度下降属于一阶优化算法,这意味着它不考虑损失函数的二阶导数。 但是,函数的曲率会影响每个学习步长的大小。梯度描述了曲线的陡度,二阶导数则测量曲线的曲率。因此,如果:
1.二阶导数= 0→曲率是线性的。 因此,步长=学习率α。
2.二阶导数> 0→曲率向上。 因此,步长<学习率α可能会导致发散。
3.二阶导数<0→曲率向下。 因此,步长>学习率α。
因此,对梯度看起来有希望的方向可能不会如此,并可能导致学习过程减慢甚至发散。
- 如果Hessian矩阵不够好,比如最大曲率的方向要比最小曲率的方向曲率大得多。 这将导致损失函数在某些方向上非常敏感,而在其他方向不敏感。 因此,有些看起来有利于梯度的方向可能不会导致损失函数发生很大变化(请参见图7)。

图7: 梯度下降未能利用包含在Hessian矩阵中的曲率信息。
- 随着每个学习步骤完成,梯度gTg的范数应该缓慢下降,因为曲线越来越平缓,曲线的陡度也会减小。 但是,由于曲线的曲率使得梯度的范数在增加。尽管如此,但我们还能够获得非常低的错误率(见图8)。

图8: 梯度范数. Source
- 在小规模数据集中,局部最小值是常见的; 然而,在大规模数据集中,鞍点更为常见。鞍点是指函数在某些方向上向上弯曲而在其他方向上向下弯曲。换句话说,鞍点看起来像是一个方向的最小值,另一个方向的最大值(见图9)。 当Hessian矩阵的特征值至少有一个是负值而其余的特征值是正值时就会发生这种情况。

图9: 鞍点
- 如前所述,选择适当的学习率是困难的。 另外,对于小批量梯度下降,我们必须在训练过程中调整学习速率,以确保它收敛到局部最小值而不是在其周围来回游荡。计算学习率的衰减率也是很难的,并且这会随着数据集不同而变化。
- 所有参数更新具有相同的学习率; 然而,我们可能更希望对一些参数执行更大的更新,因为这些参数的方向导数比其他参数更接近朝向最小值的轨迹,那么就需要针对性的设定学习率及其变化。
-
机器学习
+关注
关注
66文章
8467浏览量
133632 -
深度学习
+关注
关注
73文章
5531浏览量
122087
原文标题:机器学习优化算法「梯度下降」及其变种算法
文章出处:【微信号:thejiangmen,微信公众号:将门创投】欢迎添加关注!文章转载请注明出处。
发布评论请先 登录
相关推荐





 梯度下降算法及其变种:批量梯度下降,小批量梯度下降和随机梯度下降
梯度下降算法及其变种:批量梯度下降,小批量梯度下降和随机梯度下降












评论