使用巧妙的集成方法改进了神经网络的优化过程

传统的神经网络集成

传统上，集成组合若干不同的模型，让它们基于相同的输入做出预测。接着通过某种平均化方法决定集成的最终预测。可能是通过简单的投票或取均值，也可能是通过另一个模型，该模型基于集成模型的结果学习预测正确值或标签。岭回归是一种组合若干预测的特定方法，Kaggle竞赛冠军使用过这一方法。

集成应用于深度学习时，组合若干网络的预测以得到最终预测。通常，使用不同架构的神经网络比较好，因为不同架构的网络更可能在不同的训练样本上犯错，因而集成的收益会更大。

然而，你也可以集成同一架构的模型，并得到出乎意料的好效果。比如，在这篇快照集成的论文中，作者在训练同一个网络时保存了权重快照，在训练之后，创建了同一架构、不同权重的网络集成。这可以提升测试表现，同时也是一个非常节省开销的方法，因为你只训练一个模型，训练一次，只不过不时地保存权重。

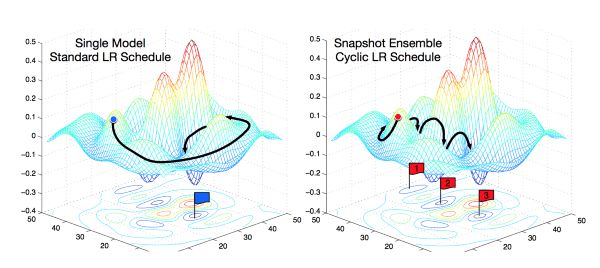
每个学习率周期末尾保存模型；图片来源：原论文

你可以阅读文章开头提到的Vitaly Bushaev的博客文章了解细节。如果你到目前为止还没有尝试过周期性学习率，那你真应该尝试一下，它正在成为当前最先进的技术，而且非常简单，算力负担也不重，可以说是在几乎不增加额外开销的前提下提供显著的增益。

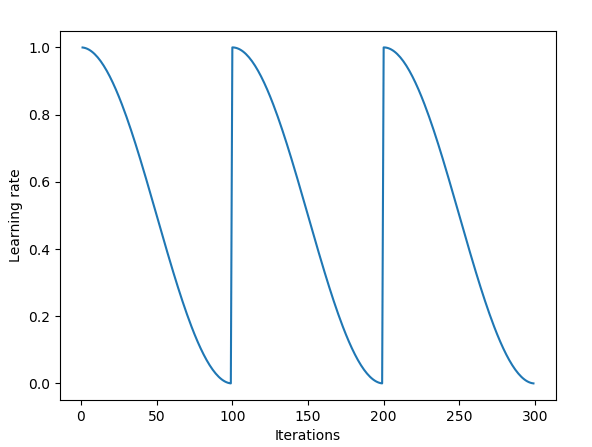
快照集成使用周期性学习率退火；图片来源：Vitaly Bushaev

上面所有的例子都是模型空间内的集成，组合若干模型，接着使用这些模型的预测以得到最终模型。

而本文开头提到的论文，作者提出的是权重空间内的集成。该方法通过组合同一网络在训练的不同阶段的权重得到一个集成，接着使用组合的权重做出预测。这一方法有两大优势：

组合权重后，我们最终仍然得到一个模型，这有利于加速预测。

该方法超过了当前最先进的快照集成。

在我们看看这一方法是如何工作之前，我们需要先理解损失平面（loss surface）和概化解（generalizable solution）。

权重空间的解

第一个重要的洞见是，一个训练好的网络是多维权重空间中的一点。对任何给定的架构而言，每个不同的网络权重组合产生一个不同的模型。任何给定架构都有无穷的权重组合，因而有无穷的解。训练神经网络的目标是找到一个特定的解（权重空间中的点），使得训练数据集和测试数据集上的损失函数的值都比较低。

在训练中，训练算法通过改变权重来改变网络并在权重空间中漫游。梯度下降算法在一个损失平面上漫游，该平面的海拔为损失函数的值。

狭窄最优和平坦最优

可视化和理解多维权重空间的几何学非常困难。与此同时，了解它又非常重要，因为随机梯度下降本质上是在训练时穿过这一高维空间中的损失平面，试图找到一个良好的解——损失平面上的一“点”，那里损失值较低。研究表明，这一平面有很多局部最优值。但这些局部最优值并不同样良好。

为了处理一个14维空间中的超平面，可视化一个3维空间，然后大声对自己说“十四”。每个人都这么做。

-- Hinton （出处：coursera课程）

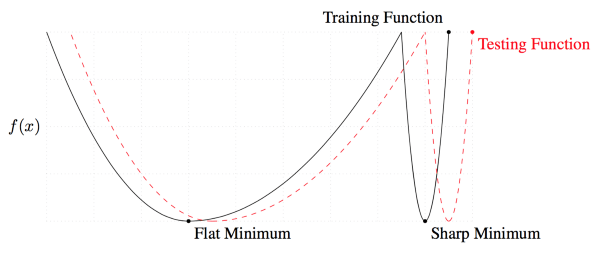
可以区分良好的解与糟糕的解的一个量度是平坦性（flatness）。背后的想法是训练数据集和测试数据集会产生相似但不是完全一样的损失平面。你可以将其想象为测试平面相对训练平面平移了一点。对一个狭窄的解而言，测试时期，损失较低的点可能因为这一平移产生变为损失较高的点。这意味着这一狭窄的解概括性不好——训练损失低，测试损失高。另一方面，对于宽而平的解而言，这一平移造成的训练损失和测试损失间的差异较小。

我解释了两种解之间的差异，因为本文关注的新方法可以导向良好、宽阔的解。

快照集成

起初，SGD会在权重空间中跳一大步。接着，由于余弦退火，学习率会降低，SGD将收敛于某个局部解，算法将保存一个模型的“快照”。接着学习率重置为高值，SGD再次迈一大步，以此类推。

快照集成的周期长度为20到40个epoch。较长的学习率周期是为了在权重空间中找到足够不同的模型，以发挥集成的优势。

快照集成表现优异，提升了模型的表现，但是快速几何集成（Fast Geometric Ensembling）效果更好。

快速几何集成（FGE）

快速几何集成和快照集成非常相似。它们的不同主要有两点。第一，快速几何集成使用线性分段周期学习率规划，而不是余弦退火。第二，FGE的周期长度要短得多——2到4个epoch。这是因为作者发现，在足够不同的模型之间，存在着损失较低的连通路径。沿着这些路径小步前进所得的模型差异较大，足够发挥集成的优势。因此，相比快照集成，FGE表现更好，搜寻模型的步调更小（步调更小使其训练更快）。

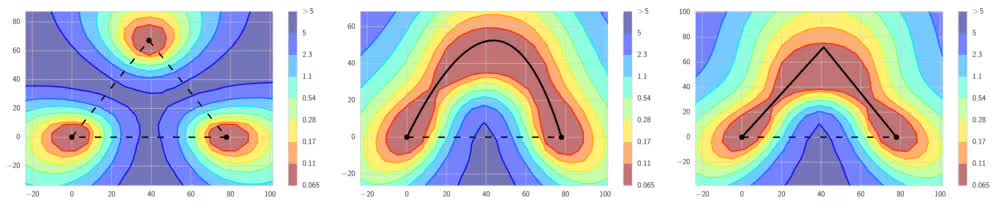
如上图左侧的图像所示，根据传统的直觉，良好的局部极小值被高损失区域分隔开来（图中虚线）。而上图中、右的图像显示，局部极小值之间存在着路径，这些路径上的损失都很低（图中实线）。FGE沿着这些路径保存快照，从而创建快照的集成。

快照集成和FGE都需要储存多个模型，接着让每个模型做出预测，之后加以平均以得到最终预测。因此，我们为集成的额外表现支付了更高的算力代价。所以天下没有免费的午餐。真的没有吗？让我们看看随机加权平均吧。

随机加权平均（SWA）

随机加权平均只需快速集合集成的一小部分算力，就可以接近其表现。SWA导向我之前提到过的广阔的极小值。在经典定义下，SWA不算集成，因为在训练的最终阶段你得到一个模型，但它的表现超过了快照集成，接近FGE。

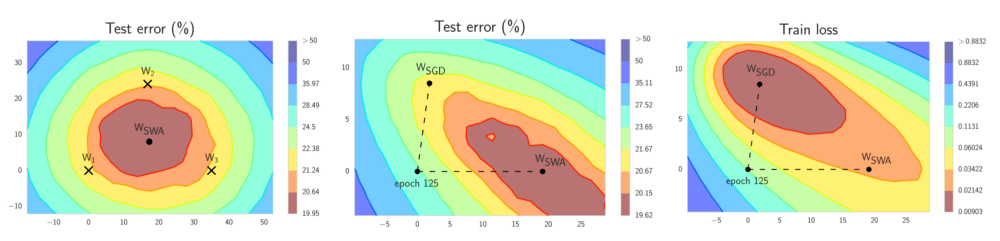
SWA的直觉来自以下由经验得到的观察：每个学习率周期得到的局部极小值倾向于堆积在损失平面的低损失值区域的边缘（上图左侧的图形中，褐色区域误差较低，点W1、W2、3分别表示3个独立训练的网络，位于褐色区域的边缘）。对这些点取平均值，可能得到一个宽阔的概化解，其损失更低（上图左侧图形中的WSWA）。

上图中间的图形显示，WSWA在测试集上的表现超越了SGD。而上图右侧的图形显示，WSWA在训练时的损失比SGD要高。结合WSWA在测试集上优于SGD的表现，这意味着尽管WSWA训练时的损失较高，它的概括性更好。

下面是SWA的工作机制。SWA只保存两个模型，而不是许多模型的集成：

第一个模型保存模型权重的平均值（wSWA）。在训练结束后，它将是用于预测的最终模型。

第二个模型（w）将穿过权重空间，基于周期性学习率规划探索权重空间。

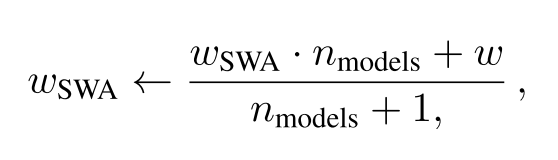
SWA权重更新公式；

在每个学习率周期的末尾，第二个模型的当前权重将用来更新第一个模型的权重（公式见上）。因此，训练阶段中，只需训练一个模型，并在内存中储存两个模型。预测时只需要平均模型，基于其进行预测将比之前描述的集成快很多，因为在集成中，你需要使用多个模型进行预测，最后进行平均。